计算复杂性(四):NP 完全性
NP完全性
- 1 多项式时间
-
- 复杂性类P
- 定理(引理34.1)
- 一种形式语言体系
- 接受、拒绝、判定
- 定理(34.2)
- 2 多项式时间 时间验证
-
- 验证算法
- 非确定性图灵机 (Non-Deterministic Turing Machine, NDTM)
- 3 NP完全性与可规约性
-
- NP 完全问题 (NP Complete, NPC)
- 可规约性
- 定理(引理34.3)
- NP完全语言
- 定理(34.4)
- 布尔组合电路
- 电路可满足性问题
- NP 完全性
- 定理(引理34.5)
- 定理(引理34.6)
- 定理(引理34.7)
- 4 NP完全性的证明
-
- 定理(引理34.8)
- 证明语言 L 是 NP 完全的方法
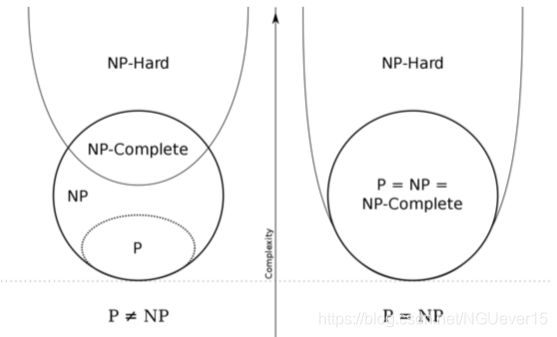
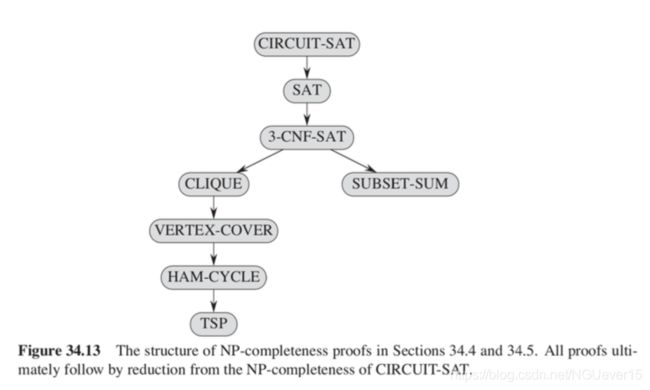
- 5 NP完全问题
- P 类问题:多项式时间内可以解决的问题。
- NP 类问题:多项式时间内可以被验证的问题,P⊆NP。
- NPC 类问题:NP 类问题中 “最难” 解决的一类问题。
判定问题与最优化问题:
现实中很多问题都是最优化问题,希望找到一个具有最佳值的可行解。
NP 完全性不适合直接应用于最优化问题,而适用于判定问题:判断一个问题的答案 “是” 或 “否”(即程序给出 “1” 或 “0” 的输出)
最优化问题 → 判定问题(SHORTEST-PATH→PATH): 求解最优问题后,直接与判定问题的 k 值比较即可。
判定问题 → 最优化问题(PATH→SHORTEST-PATH): 从 n = |V| 开 始,逐渐给最短路径加界限,例如逐个求解 k = n,k = n−1,…,k = 0 的 PATH 问题。
判定问题相比优化问题 “更容易一些”,至少 “不会更难”,如果知道判定问题是困难的,表明相应的优化问题也是困难的。
1 多项式时间
抽象问题Q 是问题实例集 I 与问题解集 S 上的二元关系。
判定问题是解为肯定或否定的那些抽象问题,也可理解为映射实例集 I 到解集 {0, 1} 的函数。
通过为将被优化的值增加一个界限,优化问题可改造成判定问题。
若能证明判定问题是难的,则原优化问题也是难的。
抽象对象集 S 的编码是从 S 到二进制串集合的一个映射 e。
具体问题是实例集为二进制串集合的问题。
如果对某具体问题的长度为 n = |i| 的问题实例 i,某算法能在不超 过 O(T(n)) 的时间内产生问题的解,那么称该算法在时间 O(T(n)) 内解决了该具体问题。
如果对某具体问题存在常数 k 和算法 A,使得 A 在时间 O( n k n^k nk) 内解决了该具体问题,那么称该具体问题是多项式时间可解的。
复杂性类P
复杂性类 P定义为多项式时间可解的具体判定问题的集合。
可以利用编码将抽象问题映射到具体问题上:

由上述操作,对表示抽象问题实例的编码的二进制串实例,具体问题与抽象问题产生同样的解。
问题求解的效率依赖于问题的编码方式。
一元编码只需线性时间的算法,
若采用二进制编码,则可能需要指数时间(伪多项式时间)。
定理(引理34.1)
结论:
对一个抽象问题的实例,无论采用二进制或三进制来进行编 码,对其 “复杂度” 都没有影响(但如果对实例进行一元编码,则其复 杂度可能会变化)。
因此,以后的分析均假定一个整数的编码与其二进制表示是多项式相关的,称为其标准编码。G 的标准编码记为 ⟨G⟩。
一种形式语言体系
接受、拒绝、判定
定理(34.2)
2 多项式时间 时间验证

无向图 G = (V, E) 的哈密顿圈是包含 V 中每个顶点的简单圈。存在哈 密顿圈的图称为哈密顿图,否则称为非哈密顿图。
验证算法
复杂性类 NP(Nondeterministic Polynomial Time,非确定性多项式时 间) 是可由多项式时间算法验证的语言的类。
更精确地,语言 L ∈ NP 当且仅当存在具有两个输入的多项式时间算法 A 和常数 c,使得:

非确定性图灵机 (Non-Deterministic Turing Machine, NDTM)
NP: 当一个判定问题存在一个 O(nk) 时间复杂度的非确定性算法 (non-deterministic algorithm) 时,则称此问题落在 NP 的集合中。
非确定型图灵机中的多项式时间可判定的问题在确定性图灵机中多项
式时间可验证。
3 NP完全性与可规约性
NP 完全问题 (NP Complete, NPC)
- NP 问题中存在一类特殊的问题:NP 完全问题。
- 如果任意 NP 完全问题是多项式时间可解的,那么 NP 中的每个问 题都是多项式时间可解的,即 P=NP。
- 在某种意义下,NP 完全语言是 NP 中最难判定的语言。
- 使用多项式时间可归约性的概念可比较语言的相对难度。
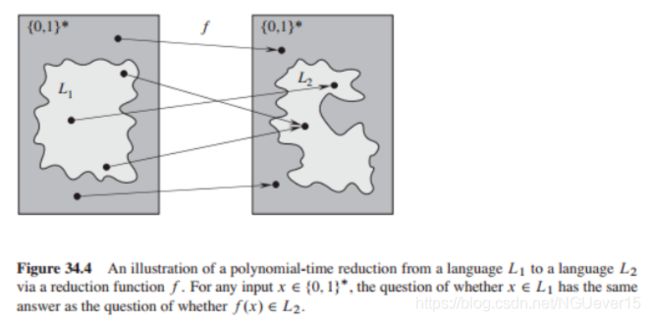
可规约性
定理(引理34.3)

L 1 可 规 约 到 L 2 L_1可规约到L_2 L1可规约到L2
**证明思路:**设 A2 是判定 L2 的多项式时间算法,F 是计算归约函数 f 的 多项式时间归约算法,利用 A2, F 构造出一个可判定 L1 的多项式时间 算法。
NP完全语言

如果语言 L 满足性质 2,但不一定满足性质 1,那么称 L 是NP 难 (NP-hard)的。定义 NPC 为 NP 完全语言类。
对于NP中任意的语言L‘ ,都能多项式时间可归约到 L,但L不属于NP,那么称L 是NP难
定理(34.4)
多数理论计算机科学家对 P、NP 和 NPC 三者关系的猜想:
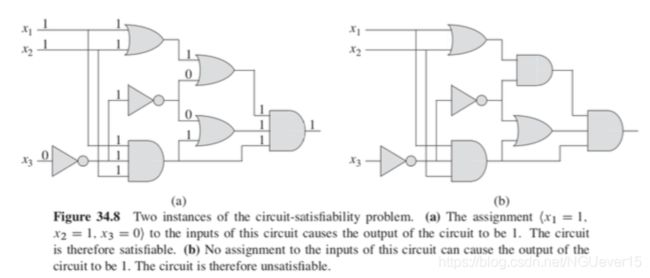
布尔组合电路
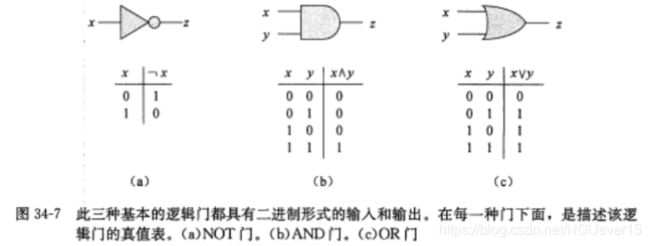
- 布尔组合元素是指有固定输入的输入和输出,执行某种良定义的函 数功能,布尔值取自集合 {0, 1}。
- AND 门,OR 门,NOT 门等简单的布尔函数称为逻辑门,其功能 可用真值表描述。
- 布尔组合电路是由一个或多个布尔组合元素通过线路连接而成。
- 对布尔组合电路的真值赋值就是一组布尔输入值。
- 如果存在一个真值赋值,使某个单输出的布尔组合电路的输出为 1,那么称该电路是可满足的,并称这个真值赋值是一个满足的赋值。
电路可满足性问题
是否存在一个输入的赋值,使得输出为1
实际应用:计算机辅助硬件优化,检查非必要的子电路。
NP 完全性

注:第一个 NP 完全问题是 1971 年 Stephen A. Cook 证明的 SAT 问题。
定理(引理34.5)
定理(引理34.6)

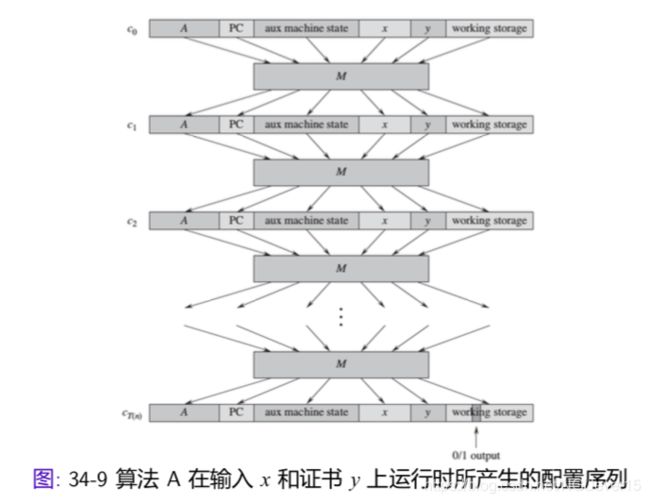
定理的形式化证明需要用到非确定性图灵机,我们采用非形式化的描述
证明:

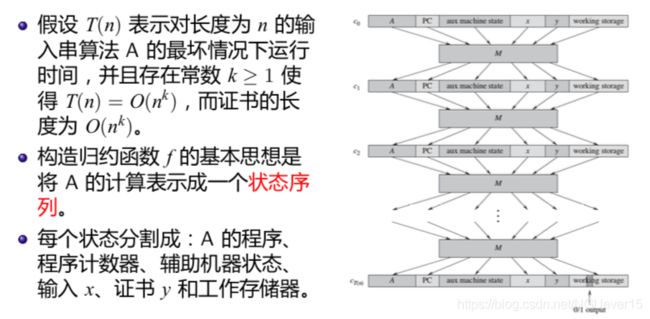

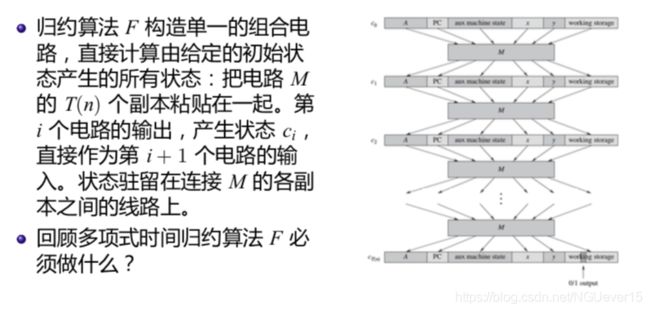
给定输入 x,F 须计算一个电路 C = f(x),使得 C 是可满足的当且 仅当存在证书 y 使 A(x, y) = 1。
归约算法 F:给定 M, A(x, y), x,计算得到电路 C(y):

定理(引理34.7)
由引理 34.5 和引理 34.6 及 NP 完全的定义立即可得:
![]()
4 NP完全性的证明
定理(引理34.8)
证明语言 L 是 NP 完全的方法
。。。 (暂时跳过)。。。