BPR贝叶斯个性化推荐算法—推荐系统基础算法（含python代码实现以及详细例子讲解）
BPR贝叶斯个性化排序算法
- 一、问题导入
- 二、显示反馈与隐式反馈
-
- 2.1 显式反馈与隐式反馈基本概念
- 2.2 显式反馈与隐式反馈的比较
- 2.3 显式反馈与隐式反馈的评价方法
-
- 2.3.1 显式反馈数据模型的评价方法
-
- 2.3.1.1 显式反馈模型介绍
- 2.3.1.2 具体例子分析
- 2.3.1.3 显示反馈数据分析
- 2.3.2 隐式反馈数据介绍
-
- 2.3.2.1 隐式反馈数据的特点
- 2.3.2.2 隐式反馈数据的处理方式
- 三、BPR算法概述
-
- 3.1 BPR算法基本概念
- 3.2 BPR算法相关定义
- 3.3 BPR建模思路
- 四、BPR算法优化
- 五、算法流程
- 六、BPR算法小结
- 七、python 代码实现
- 八、参考文章资料来源
- 九、代码文件
一、问题导入
在很多推荐场景中，我们都是基于现有的用户和商品之间的一些数据，得到用户对所有商品的评分，选择高分的商品推荐给用户，这是矩阵分解之类算法的做法，使用起来也很有效。但是在有些推荐场景中，我们是为了在千万级别的商品中推荐个位数的商品给用户，此时，我们更关心的是用户来说，哪些极少数商品在用户心中有更高的优先级，也就是排序更靠前。也就是说，我们需要一个排序算法，这个算法可以把每个用户对应的所有商品按喜好排序。BPR就是这样的一个我们需要的排序算法。一个更朴素的思想就是用户交互过的项目的优先级一定没有交互过的项目优先级高，这就是BPR算法的核心内容。
二、显示反馈与隐式反馈
2.1 显式反馈与隐式反馈基本概念
显式反馈是指：用户明确喜欢和不喜欢的物品。例如：用户对物品的评分，如电影评分。
隐式反馈是指：用户对于浏览过的物品没有明确表示喜欢或厌恶。这种类型数据只能认为全部是正反馈也即喜欢的物品。例如：用户对物品的交互行为，如浏览，购买等，现实中绝大部分数据属于隐式反馈，可以从日志中获取。
2.2 显式反馈与隐式反馈的比较
| 隐式反馈 | 显式反馈 | |
|---|---|---|
| 准确度 | 底 | 高 |
| 丰富的 | 高 | 底 |
| 获取数据 | 容易 | 困难 |
| 数据噪音 | 较难识别 | 较易识别 |
| 上下文敏感 | 是 | 是 |
| 用户偏好的表达能力 | 只有正样本 | 包含正负样本 |
| 评估比较标准 | 相对比较 | 绝对比较 |
2.3 显式反馈与隐式反馈的评价方法
2.3.1 显式反馈数据模型的评价方法
2.3.1.1 显式反馈模型介绍
| 模型判定推荐的 | 模型判定不推荐的 | |
|---|---|---|
| 测试集中被推荐的用户满意的商品(被检索到) | True positives(TP 正类判断为正类)（搜到的也想要的） | False negatives（FN 正类判断为负类）（没搜到，然而实际想要的） |
| 测试集中不被推荐的用户满意的商品，即用户不满意的商品（未被检索到） | False positives（FP 负类判断为正类）（搜到的但没用的） | True negatives（TN 负类判定为负类）（没搜到也没用的） |
这个表格就是机器学习里面最常见的混淆矩阵，用来评判模型的好坏。
2.3.1.2 具体例子分析
先假定一个具体场景作为例子。
假如某个班级有男生80人,女生20人,共计100人.目标是找出所有女生.
某人挑选出50个人,其中20人是女生,另外还错误的把30个男生也当作女生挑选出来了.
作为评估者的你需要来评估(evaluation)下他的工作。
我们需要先需要定义TP,FN,FP,TN四种分类情况。
按照前面例子,我们需要从一个班级中的人中寻找所有女生,如果把这个任务当成一个分类器的话,那么女生就是我们需要的,而男生不是,所以我们称女生为"正类",而男生为"负类"。
| 相关(Relevant),正类 | 无关(NonRelevant),负类 | |
|---|---|---|
| 被检索到(Retrieved) | TP=20 true positives(TP 正类判定为正类,例子中就是正确的判定"这位是女生") | FP=30 false positives(FP 负类判定为正类,“存伪”,例子中就是分明是男生却判断为女生) |
| 未被检索到(Not Retrieved) | FN=0 false negatives(FN 正类判定为负类,“去真”,例子中就是,分明是女生,这哥们却判断为男生–梁山伯同学犯的错就是这个) | TN=50 true negatives(TN 负类判定为负类,也就是一个男生被判断为男生) |
通过这张表,我们可以很容易得到例子中这几个分类的值:TP=20,FP=30,FN=0,TN=50。
2.3.1.3 显示反馈数据分析
我们可以通过计算模型分类的准确率，和召回率进来通过计算F-Measure的值来对模型分类的好坏进行评价。
下面结合例子中这几个分类的值:TP=20,FP=30,FN=0,TN=50介绍准确率，召回率，和F-measure的概念与计算方法。
1．准确率
准确率（precision）又称“精度”，“正确率”。的公式是 P = T P T P + F P P=\frac{TP}{TP+FP} P=TP+FPTP，它计算的是所有被检索到的item（TP+FP）中,“应该被检索到的item（TP）”占的比例。
在例子中就是希望知道分类得到的所有人中,正确的人(也就是女生)占有的比例.所以其precision也就是40%(20女生/(20女生+30误判为女生的男生)).
2．召回率
召回率（recall）又称“查全率”的公式是 R = T P T P + F N R=\frac{TP}{TP+FN} R=TP+FNTP ，它计算的是所有检索的tem（TP）占所有"应该被检索到的item（TP+FN）"的比例。
在例子中就是希望知道此君得到的女生占本班中所有女生的比例,所以其recall也就是100%(20女生/(20女生+ 0 误判为男生的女生))
3. 准确率与召回率的关系
“精确率”与“召回率”虽然没有必然的关系（从上面公式中可以看到），然而在大规模数据集合中，这两个指标却是相互制约的。
由于“检索策略”并不完美，希望更多相关的文档被检索到时，放宽“检索策略”时，往往也会伴随出现一些不相关的结果，从而使准确率受到影响。
而希望去除检索结果中的不相关文档时，务必要将“检索策略”定的更加严格，这样也会使有一些相关的文档不再能被检索到，从而使召回率受到影响。
凡是涉及到大规模数据集合的检索和选取，都涉及到“召回率”和“精确率”这两个指标。而由于两个指标相互制约，我们通常也会根据需要为“检索策略”选择一个合适的度，不能太严格也不能太松，寻求在召回率和精确率中间的一个平衡点。这个平衡点由具体需求决定。
4. F-Measure值
F-Measure又称为F-Score是一种统计量，是IR（信息检索）领域的常用的一个评价标准，常用于评价分类模型的好坏。它的计算公式为 F β = ( β 2 + 1 ) P R β 2 ⋅ P + R F_{\beta}=\frac{(\beta^{2}+1)PR}{\beta^2\cdot P+R} Fβ=β2⋅P+R(β2+1)PR，其中β是参数 , R是召回率（recall）P是准确率（precision）。当参数β=1时，就是最常见的F1-Measure了： F 1 = 2 P ⋅ R R + P F_{1}=\frac{2P \cdot R}{R+P} F1=R+P2P⋅R，此时F1综合了P和R的效果，当F1较高时则能说明试验方法比较有效。
2.3.2 隐式反馈数据介绍
2.3.2.1 隐式反馈数据的特点
隐性反馈数据有诸多弊端，例如不明确，具有噪点数据，但是由于他广泛存在，我们有时甚至只能利用它，所以还是要详细研究一下，通过对隐式反馈的合理降噪以及数据修剪来提升物品推荐的可行度。
显性反馈数据可以看出用户对某一物品的偏好值，例如评分机制，8分和10分的区别，而隐性反馈数据没办法衡量偏好值，只能认为用户浏览同一内容越多，越有可能喜好这个内容，也即置信度越大。
2.3.2.2 隐式反馈数据的处理方式
在使用隐式反馈的情况下，我们会发现观察到的数据均为正例（因为用户对物品交互过才会被观察到），而那些没有被观察到的数据（即用户还没有产生行为的物品），分为两种情况，一种是用户对该物品确实没有星期（负类），另一种是缺失值（即用户以后可能会产生行为的物品），而在传统的个性化推荐中通常是计算用户u对物品i的个性化分数，然后根据个性化分数进行排序。而其处理数据的方式为把所有观察到的隐式反馈作为正类，而其余数据作为负类。
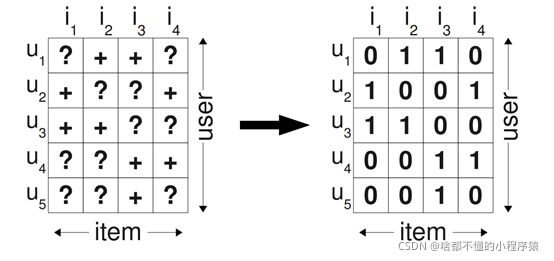
在负类被填零的情况下，我们优化目标变成了希望在预测时观测到的数据预测为1，其余的均为0，于是产生的问题是，我们希望模型在以后预测的缺失值，在训练时却都被认为时负类数据。因此这个模型训练的足够好，那么最总都得到的结果就是这些未观察的样本最后预测值都是0.
而针对与BPR算法是根据隐式反馈数据来进行比较的，通过对问题进行贝叶斯分析得到的最大后验概率来对item进行排序，进而产生推荐。
三、BPR算法概述
3.1 BPR算法基本概念
BPR（Bayesian Personalized Ranking），中文名称为贝叶斯个性化排序，是当下推荐系统中常用的一种推荐算法。与其他的基于用户评分矩阵的方法不同的是BPR主要采用用户的隐式反馈（如点击、收藏、加入购物车等），通过对问题进行贝叶斯分析得到的最大后验概率来对item进行排序，进而产生推荐。
3.2 BPR算法相关定义
U代表所有用户user集合；I代表所有物品item集合；
S代表所有用户的隐式反馈， 。如下图所示，只要用户对某个物品产生过行为（如点击、收藏、加入购物车等），就标记为+，所有+样本构成了S。那些为观察到的数据（即用户没有产生行为的数据）标记为？。
I u + = { i ∈ I : ( u , i ) ∈ S } I^{+}_{u}=\{{i\in I:(u,i)\in S}\} Iu+={i∈I:(u,i)∈S}代表了用户u产生过行为的物品集合
U i + = { u ∈ U : ( u , i ) ∈ S } U^{+}_{i}=\{{u\in U:(u,i)\in S}\} Ui+={u∈U:(u,i)∈S}代表了对物品i产生过行为的用户集合
| U/I | i1 | i2 | i3 | i4 |
|---|---|---|---|---|
| u1 | ？ | + | + | ？ |
| u2 | + | ？ | ？ | + |
| u3 | + | + | ？ | ？ |
| u4 | ？ | ？ | + | + |
| u5 | ？ | ？ | + | ？ |
这里我们假设：
1. 一是每个用户之间的偏好行为相互独立，即用户u在商品i和j之间的偏好和其他用户无关。
2. 二是同一用户对不同物品的偏序相互独立，也就是用户u在商品i和j之间的偏好和其他的商品无关。
其中用 i ≻ u j i\succ_{u}j i≻uj表示用户u在物品i和物品j之间更偏向与物品i
在BPR中，这个排序关系符号 ≻ u \succ_{u} ≻u满足完全性，反对称性和传递性，即对于用户集U和物品集I：
完整性： ∀ i , j ∈ I : i ≠ j ⇛ i ≻ u j ∪ j ≻ u i \forall i,j \in I:i \ne j \Rrightarrow i\succ_{u}j \cup j \succ_{u}i ∀i,j∈I:i=j⇛i≻uj∪j≻ui
反对称性： ∀ i , j ∈ I : i ≻ u j ∩ j ≻ u i ⇒ i = j \forall i,j \in I:i\succ_{u}j \cap j \succ_{u}i \Rightarrow i = j ∀i,j∈I:i≻uj∩j≻ui⇒i=j
传递性： ∀ i , j , k ∈ I : i ≻ u j ∪ j ≻ u k ⇒ i ≻ u k \forall i,j,k \in I: i\succ_{u}j \cup j \succ_{u}k \Rightarrow i\succ_{u}k ∀i,j,k∈I:i≻uj∪j≻uk⇒i≻uk
3.3 BPR建模思路
在BPR算法中，我们将任意用户u对应的物品进行标记，如果用户u在同时有物品i和j的时候对i产生了行为，那么我们就得到了一个三元组
那么如下图所示，基于观察到的数据S构建数据集 D s D_{s} Ds，通过对每个用户，可以构建 I × I I \times I I×I的偏好矩阵。所有用户的偏好对构成了训练集 D s = U × I × I D_{s}=U \times I \times I Ds=U×I×I
D s = { ( u , i , j ) ∣ i ∈ I u + ∧ j ∈ I ∖ I u + } D_{s}=\{(u,i,j) \mid i \in I^{+}_{u} \land j \in I \setminus I^{+}_{u} \} Ds={(u,i,j)∣i∈Iu+∧j∈I∖Iu+}
那么注意，对于每个三元组样本
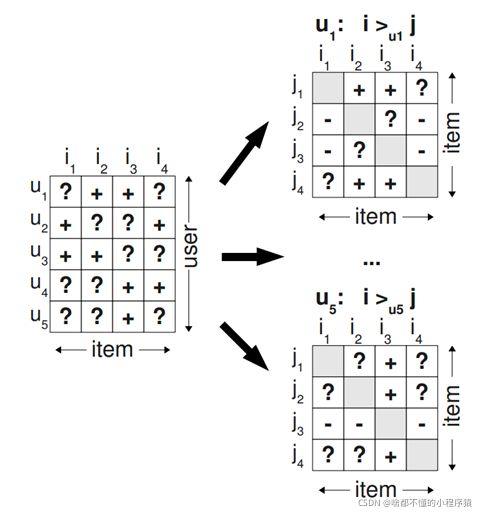
同时，BPR也用了类似矩阵分解模型，这里BPR对于用户集U和物品集I的对应的U×I的预测排序矩阵 X ‾ \overline X X，我们期望得到两个分解后的用户矩阵W(|U|×k)和物品矩阵H(|I|×k)，满足 X ‾ = W H T \overline X =WH^{T} X=WHT
这里的k和矩阵分解模型，也是自己定义的，一般远远小于|U|,|I|。
由于BPR是基于用户维度的，所以对于任意一个用户u，对应的任意一个物品i我们期望有： x ‾ u i = w u ⋅ h i = ∑ f = 1 k w u f h i f \overline x_{ui}=w_{u}\cdot h_{i}=\sum_{f=1}^{k}w_{uf}h_{if} xui=wu⋅hi=∑f=1kwufhif
最终我们的目标，是希望寻找合适的矩阵W,H，让 和X最相似。读到这里，也许你会说，这和矩阵分解模型没有什么区别啊？的确，现在还看不出，下面我们来看看BPR的算法优化思路，就会慢慢理解和矩阵分解模型有什么不同了。
四、BPR算法优化
BPR 基于最大后验估计 P ( W , H ∣ ≻ u P(W,H \mid \succ_{u} P(W,H∣≻u)来求解模型参数W,H,这里我们用θ来表示参数W和H, ≻ u \succ_{u} ≻u代表用户u对应的所有商品的全序关系,则优化目标是 P ( θ ∣ ≻ u ) P(\theta \mid \succ_{u}) P(θ∣≻u) 。根据贝叶斯公式，我们有：
由于我们求解假设了用户的排序和其他用户无关，那么对于任意一个用户u来说， P ( ≻ u ) P(\succ_{u}) P(≻u)对所有的物品一样，所以有：
这个优化目标转化为两部分。第一部分和样本数据集D有关，第二部分和样本数据集D无关。
对于第一部分，由于我们假设每个用户之间的偏好行为相互独立，同一用户对不同物品的偏序相互独立，所以有：
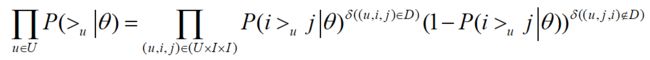
其中，当b为真时，δ（b）=1；否则， δ（b）=0.
根据上面讲到的完整性和反对称性，优化目标的第一部分可以简化为：
而对于 这个概率，我们可以使用下面这个式子来代替:
其中，σ(x)是sigmoid函数。这里你也许会问，为什么可以用这个sigmoid函数来代替呢? 其实这里的代替可以选择其他的函数，不过式子需要满足BPR的完整性，反对称性和传递性。原论文作者这么做除了是满足这三个性质外，另一个原因是为了方便优化计算。
对于 x ‾ u i j ( θ ) \overline x_{uij}(\theta) xuij(θ)这个式子，我们要满足当 i ≻ u j i\succ_{u}j i≻uj时， x ‾ u i j ( θ ) \overline x_{uij}(\theta) xuij(θ)>0 , 反之当 j ≻ u i j\succ_{u}i j≻ui时， x ‾ u i j ( θ ) \overline x_{uij}(\theta) xuij(θ)<0 ，最简单的表示这个性质的方法就是
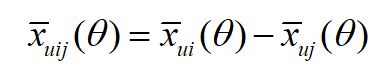
而 x ‾ u i \overline x_{ui} xui , x ‾ u j \overline x_{uj} xuj ，就是我们的矩阵 X ‾ \overline X X对应位置的值。这里为了方便,我们不写θ,这样上式可以表示为: 
注意上面的这个式子也不是唯一的，只要可以满足上面提到的当 i ≻ u j i\succ_{u}j i≻uj时， x ‾ u i j ( θ ) > 0 \overline x_{uij}(\theta)>0 xuij(θ)>0 ，以及对应的相反条件即可。这里我们仍然按原论文的式子来。
最终，我们的第一部分优化目标转化为：
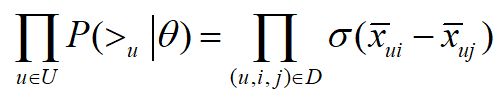
对于第二部分P(θ)，原作者大胆使用了贝叶斯假设，即这个概率分布符合正太分布，且对应的均值是0，协方差矩阵是 λ θ I \lambda_{\theta}I λθI,即
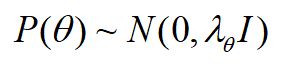
原作者为什么这么假设呢？个人觉得还是为了优化方便，因为后面我们做优化时，需要计算 l n P ( θ ) lnP(\theta) lnP(θ)，而对于上面假设的这个多维正态分布，其对数和 ∣ ∣ θ ∣ ∣ 2 \mid \mid \theta \mid \mid^{2} ∣∣θ∣∣2成正比。即：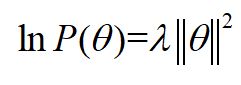 
最终对于我们的最大对数后验估计函数
这个式子可以用梯度上升法或者牛顿法等方法来优化求解模型参数。如果用梯度上升法，对θ求导，我们有：
由于
这样我们可以求出：
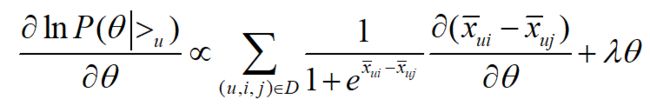
五、算法流程
下面简要总结下BPR的算法训练流程：
输入：训练集D三元组，梯度步长α，正则化参数λ,分解矩阵维度k。
输出：模型参数，矩阵W,H
1. 随机初始化矩阵W,H
2. 迭代更新模型参数：
3. 如果W,H收敛，则算法结束，输出W,H，否则回到步骤2.
当我们拿到W,H后，就可以计算出每一个用户u对应的任意一个商品的排序分： x ‾ u i = w i ⋅ h i \overline x_{ui} = w_{i} \cdot h_{i} xui=wi⋅hi，最终选择排序分最高的若干商品输出。
六、BPR算法小结
BPR是基于矩阵分解的一种排序算法，但是和funkSVD之类的算法比，它不是做全局的评分优化，而是针对每一个用户自己的商品喜好分贝做排序优化。因此在迭代优化的思路上完全不同。同时对于训练集的要求也是不一样的，funkSVD只需要用户物品对应评分数据二元组做训练集，而BPR则需要用户对商品的喜好排序三元组做训练集。
七、python 代码实现
以下代码是BPR的主函数代码，读者拷贝后可以把文件命名为BPR_basical.py
# ！/usr/bin/env python
# @Time:2021/4/6 19:21
# @Author:华阳
# @File:Basical BPR.py
# @Software:PyCharm
import random
from collections import defaultdict
import numpy as np
from sklearn.metrics import roc_auc_score
import scores
'''
函数说明:BPR类（包含所需的各种参数）
Parameters:
无
Returns:
无
'''
class BPR:
#用户数
user_count = 943
#项目数
item_count = 1682
#k个主题,k数
latent_factors = 20
#步长α
lr = 0.01
#参数λ
reg = 0.01
#训练次数
train_count = 10000
#训练集
train_data_path = 'train.txt'
#测试集
test_data_path = 'test.txt'
#U-I的大小
size_u_i = user_count * item_count
# 随机设定的U，V矩阵(即公式中的Wuk和Hik)矩阵
U = np.random.rand(user_count, latent_factors) * 0.01 #大小无所谓
V = np.random.rand(item_count, latent_factors) * 0.01
biasV = np.random.rand(item_count) * 0.01
#生成一个用户数*项目数大小的全0矩阵
test_data = np.zeros((user_count, item_count))
print("test_data_type",type(test_data))
#生成一个一维的全0矩阵
test = np.zeros(size_u_i)
#再生成一个一维的全0矩阵
predict_ = np.zeros(size_u_i)
#获取U-I数据对应
'''
函数说明：通过文件路径，获取U-I数据
Paramaters:
输入要读入的文件路径path
Returns:
输出一个字典user_ratings，包含用户-项目的键值对
'''
def load_data(self, path):
user_ratings = defaultdict(set)
with open(path, 'r') as f:
for line in f.readlines():
u, i = line.split(" ")
u = int(u)
i = int(i)
user_ratings[u].add(i)
return user_ratings
'''
函数说明：通过文件路径，获取测试集数据
Paramaters：
测试集文件路径path
Returns:
输出一个numpy.ndarray文件（n维数组）test_data,其中把含有反馈信息的数据置为1
'''
#获取测试集的评分矩阵
def load_test_data(self, path):
file = open(path, 'r')
for line in file:
line = line.split(' ')
user = int(line[0])
item = int(line[1])
self.test_data[user - 1][item - 1] = 1
'''
函数说明：对训练集数据字典处理，通过随机选取，（用户，交互，为交互）三元组，更新分解后的两个矩阵
Parameters：
输入要处理的训练集用户项目字典
Returns：
对分解后的两个矩阵以及偏置矩阵分别更新
'''
def train(self, user_ratings_train):
for user in range(self.user_count):
# 随机获取一个用户
u = random.randint(1, self.user_count) #找到一个user
# 训练集和测试集的用于不是全都一样的,比如train有948,而test最大为943
if u not in user_ratings_train.keys():
continue
# 从用户的U-I中随机选取1个Item
i = random.sample(user_ratings_train[u], 1)[0] #找到一个item，被评分
# 随机选取一个用户u没有评分的项目
j = random.randint(1, self.item_count)
while j in user_ratings_train[u]:
j = random.randint(1, self.item_count) #找到一个item，没有被评分
#构成一个三元组（uesr,item_have_score,item_no_score)
# python中的取值从0开始
u = u - 1
i = i - 1
j = j - 1
#BPR
r_ui = np.dot(self.U[u], self.V[i].T) + self.biasV[i]
r_uj = np.dot(self.U[u], self.V[j].T) + self.biasV[j]
r_uij = r_ui - r_uj
loss_func = -1.0 / (1 + np.exp(r_uij))
# 更新2个矩阵
self.U[u] += -self.lr * (loss_func * (self.V[i] - self.V[j]) + self.reg * self.U[u])
self.V[i] += -self.lr * (loss_func * self.U[u] + self.reg * self.V[i])
self.V[j] += -self.lr * (loss_func * (-self.U[u]) + self.reg * self.V[j])
# 更新偏置项
self.biasV[i] += -self.lr * (loss_func + self.reg * self.biasV[i])
self.biasV[j] += -self.lr * (-loss_func + self.reg * self.biasV[j])
'''
函数说明：通过输入分解后的用户项目矩阵得到预测矩阵predict
Parameters:
输入分别后的用户项目矩阵
Returns：
输出相乘后的预测矩阵，即我们所要的评分矩阵
'''
def predict(self, user, item):
predict = np.mat(user) * np.mat(item.T)
return predict
#主函数
def main(self):
#获取U-I的{1:{2,5,1,2}....}数据
user_ratings_train = self.load_data(self.train_data_path)
#获取测试集的评分矩阵
self.load_test_data(self.test_data_path)
#将test_data矩阵拍平
for u in range(self.user_count):
for item in range(self.item_count):
if int(self.test_data[u][item]) == 1:
self.test[u * self.item_count + item] = 1
else:
self.test[u * self.item_count + item] = 0
#训练
for i in range(self.train_count):
self.train(user_ratings_train) #训练10000次完成
predict_matrix = self.predict(self.U, self.V) #将训练完成的矩阵內积
# 预测
self.predict_ = predict_matrix.getA().reshape(-1) #.getA()将自身矩阵变量转化为ndarray类型的变量
print("predict_new",self.predict_)
self.predict_ = pre_handel(user_ratings_train, self.predict_, self.item_count)
auc_score = roc_auc_score(self.test, self.predict_)
print('AUC:', auc_score)
# Top-K evaluation
scores.topK_scores(self.test, self.predict_, 5, self.user_count, self.item_count)
'''
函数说明：对结果进行修正，即用户已经产生交互的用户项目进行剔除，只保留没有产生用户项目的交互的数据
Paramaters:
输入用户项目字典集，以及一维的预测矩阵，项目个数
Returns:
输出修正后的预测评分一维的预测矩阵
'''
def pre_handel(set, predict, item_count):
# Ensure the recommendation cannot be positive items in the training set.
for u in set.keys():
for j in set[u]:
predict[(u - 1) * item_count + j - 1] = 0
return predict
if __name__ == '__main__':
#调用类的主函数
bpr = BPR()
bpr.main()
以下代码是计算模型指标的代码。注意！！！读者拷贝时，一定要记得把文件命名为scores.py同时与BPR_basical.py文件放在同一个子目录下。否则，运行BPR_basical文件会找不到scores模块。数据集放在百度网盘里了。链接：https://pan.baidu.com/s/1qe8fXbLxB25g_aH-SlN5Dg ，提取码：uf6c。读者自行使用。
# -*- coding: utf-8 -*-
"""scores.ipynb
Automatically generated by Colaboratory.
Original file is located at
https://colab.research.google.com/drive/17qoo1U4Iw58GRDDIyCaB2GmbRUg1gTPd
"""
import heapq
import numpy as np
import math
#计算项目top_K分数
def topK_scores(test, predict, topk, user_count, item_count):
PrecisionSum = np.zeros(topk+1)
RecallSum = np.zeros(topk+1)
F1Sum = np.zeros(topk+1)
NDCGSum = np.zeros(topk+1)
OneCallSum = np.zeros(topk+1)
DCGbest = np.zeros(topk+1)
MRRSum = 0
MAPSum = 0
total_test_data_count = 0
for k in range(1, topk+1):
DCGbest[k] = DCGbest[k - 1]
DCGbest[k] += 1.0 / math.log(k + 1)
for i in range(user_count):
user_test = []
user_predict = []
test_data_size = 0
for j in range(item_count):
if test[i * item_count + j] == 1.0:
test_data_size += 1
user_test.append(test[i * item_count + j])
user_predict.append(predict[i * item_count + j])
if test_data_size == 0:
continue
else:
total_test_data_count += 1
predict_max_num_index_list = map(user_predict.index, heapq.nlargest(topk, user_predict))
predict_max_num_index_list = list(predict_max_num_index_list)
hit_sum = 0
DCG = np.zeros(topk + 1)
DCGbest2 = np.zeros(topk + 1)
for k in range(1, topk + 1):
DCG[k] = DCG[k - 1]
item_id = predict_max_num_index_list[k - 1]
if user_test[item_id] == 1:
hit_sum += 1
DCG[k] += 1 / math.log(k + 1)
# precision, recall, F1, 1-call
prec = float(hit_sum / k)
rec = float(hit_sum / test_data_size)
f1 = 0.0
if prec + rec > 0:
f1 = 2 * prec * rec / (prec + rec)
PrecisionSum[k] += float(prec)
RecallSum[k] += float(rec)
F1Sum[k] += float(f1)
if test_data_size >= k:
DCGbest2[k] = DCGbest[k]
else:
DCGbest2[k] = DCGbest2[k-1]
NDCGSum[k] += DCG[k] / DCGbest2[k]
if hit_sum > 0:
OneCallSum[k] += 1
else:
OneCallSum[k] += 0
# MRR
p = 1
for mrr_iter in predict_max_num_index_list:
if user_test[mrr_iter] == 1:
break
p += 1
MRRSum += 1 / float(p)
# MAP
p = 1
AP = 0.0
hit_before = 0
for mrr_iter in predict_max_num_index_list:
if user_test[mrr_iter] == 1:
AP += 1 / float(p) * (hit_before + 1)
hit_before += 1
p += 1
MAPSum += AP / test_data_size
print('MAP:', MAPSum / total_test_data_count)
print('MRR:', MRRSum / total_test_data_count)
print('Prec@5:', PrecisionSum[4] / total_test_data_count)
print('Rec@5:', RecallSum[4] / total_test_data_count)
print('F1@5:', F1Sum[4] / total_test_data_count)
print('NDCG@5:', NDCGSum[4] / total_test_data_count)
print('1-call@5:', OneCallSum[4] / total_test_data_count)
return
原文链接：https://blog.csdn.net/weixin_46099084/article/details/109011670
八、参考文章资料来源
1、 https://www.cnblogs.com/linglanhuakai/p/14318807.html
2、 https://baike.baidu.com/item/f-measure/913107?fr=aladdin
3、 https://blog.csdn.net/weixin_46099084/article/details/109011670
4、 https://www.cnblogs.com/pinard/p/9128682.html#commentform
5、 https://blog.csdn.net/weixin_46099084/article/details/109011670
九、代码文件
小程序员将代码文件和相关素材整理到了百度网盘里，因为文件大小基本不大，大家也不用担心限速问题。后期小程序员有能力的话，将在gitee或者github上上传相关素材。
链接：https://pan.baidu.com/s/1Ce14ZQYEYWJxhpNEP1ERhg?pwd=7mvf
提取码：7mvf