线段树的修改和求和

        网上有很多讲线段树原理的文章，如果你是第一次接触【线段树】这种数据结构，看这些文章估计会把你脑子弄得很晕。强烈推荐直接看这个视频：线段树；

1.线段树有什么用？

我们可以先看一个例子；

给你一个很大的数组nums，现在有个需求，给定一个区间[left,right]，求该区间nums的元素和:nums[left] +nums[left+1] +…+nums[right];

常规做法直接for循环叠加就可以了；那有没有一种更高效的做法呢？
我们可以设计一种结构，在保存数据的同时，把区间的值也存储起来，这样在查询区间元素的和，就可以直接得到答案，不用再累加求和了。

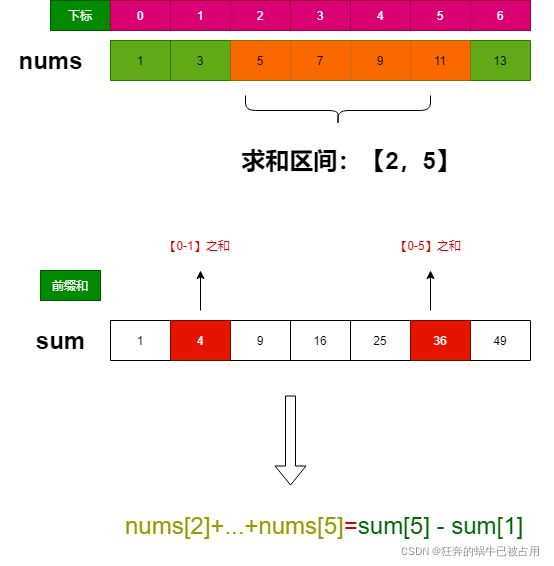
方法一：求前缀和

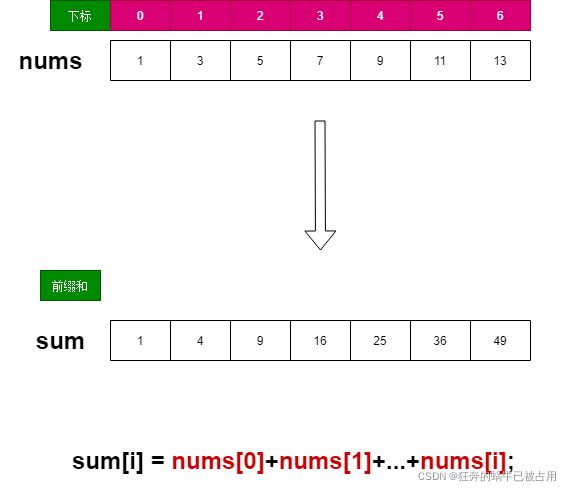
sum数组的第i元素是nums数组【0-i】元素的和；有了sum数组之后，可以很简单求任意区间和了；

代码：

//前缀和
public int[] preSum(int[] nums){
	int len =  nums.length;
	int[] sum = new int[len];
	sum[0]= nums[0];
	for(int i = 1 ;i < len ;i++){
		sum[i] = sum[i-1] + nums[i];
	}
	return sum;
}

//求nums区间和[left,right]
public int getRegSum(int[] sum,int left,int right){
	if(left == 0)return sum[right];
	return sum[right] - sum[left-1];
}

        前缀和可以解决求数组任意区间之和的问题，但同时也造成了另一种麻烦，如果nums[i]数组的值有变动，sum[i]到sum[len-1]的所有值都要修改；最差的结果是修改nums[0]的值会造成sum数组所有值的修改；所以在使用前缀和时需要考虑数组是否经常修改；

方法二：线段树

上面讲到的前缀和求nums数组区间和比较极端；那有没有一种方法，能够平衡一些呢？ 唉，线段树就出来了；
前缀和sum数组是保存了[0,0],[0,1]…[0,len-1]区间上的和；因此改动了nums中index =i的值，sum的[i,len-1]区间都受到了影响需要修改；优缺点都非常明显。
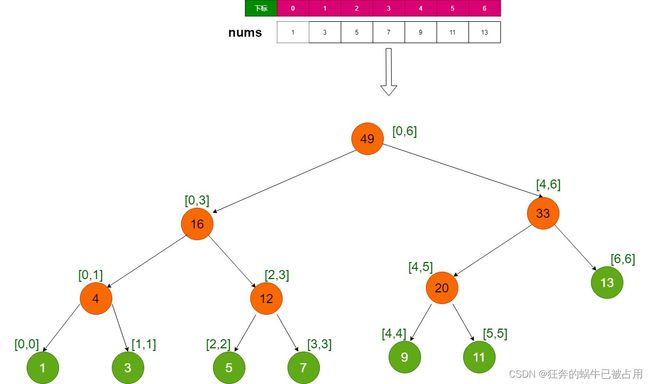
线段树的原理：递归的将数组二分成左右2个区间，分别计算左右区间的值求和保存；递归出口：区间只有一个元素；

看图：

• 橙色节点（非叶子节点）： 存储区间的长度至少是2，存储2个及以上的nums元素值之和；
• 浅绿色节点（叶子节点）： 有一个特点区间长度是1,只存储单个的nums元素值；

看上面的图就可以很清楚的知道，即使修改了nums元素值，在上面的结构中我们修改的次数也是明显减少的；当然在求取任意区间和的时候，这种树结构，就没有前缀和那么快了；

与前缀和一样，线段树也使用数组来保存；

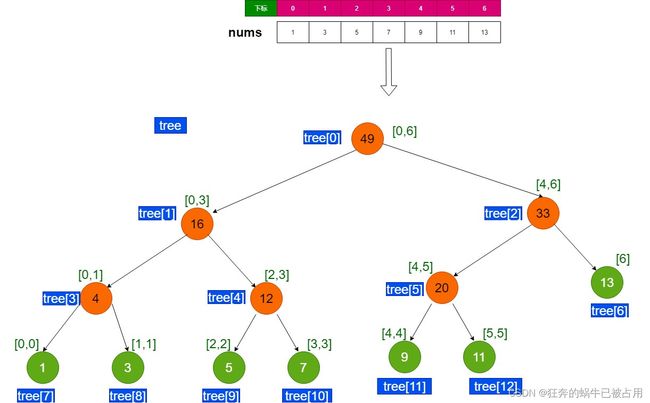
虽然使用的是数组来保存，但使用的存储逻辑是二叉树，因此在代码时要时刻注意这一点；
看上图，思路就是利用递归二分，不断的将整个nums数组分成左右两部分，直到nums数组的区间大小等于1，不能再二分为止；然后回溯分别找到左右分支的值求和保存到树顶；

看上图，父节点与左右子节点的关系：

int p = node;//父节点
int left  = 2 * p + 1;
int right = 2 * p + 2;

原理

线段树构造的原理：递归的将数组二分成左右2个区间，分别计算左右区间的值求和保存；递归出口：区间只有一个元素；

构建线段树

构建tree时，从根节点（tree[0]）开始递归构造二叉树；
出口：nums的区间长度为1；

/*
	start,end ---->表示nums的区间
	node：tree的节点；
	tree[node] 的值 : 对应nums数组的【start，end】区间之和；
	tree[node] = tree[left]+tree[right]
*/
public void buildTree(int[] nums,int[] tree,int node,int start,int end){
	if(start == end){//叶子节点
		tree[node] = nums[start];
		return;
	}
	int mid = (start + end)/2;
	int leftNode  =  2 * node + 1;
	int rightNode =  2 * node + 2;
	buildTree(nums,tree,leftNode,start,mid);
	buildTree(nums,tree,rightNode,mid+1,end);
	tree[node] = tree[leftNode]+tree[leftNode];
}

对上面参数做一个解释：
node：数据结构上是tree数组的下标；在逻辑上tree数组是一个二叉树，node在逻辑上看作是二叉树的一个节点；
对上面的tree[node]：
tree[node]的值，在对应nums数组时：

• tree[node] = nums[start] + nums[start+1] +…+nums[end];

在tree数组中（二叉树）：

• tree[node] = tree[leftNode] + tree[rightNode];

修改线段树

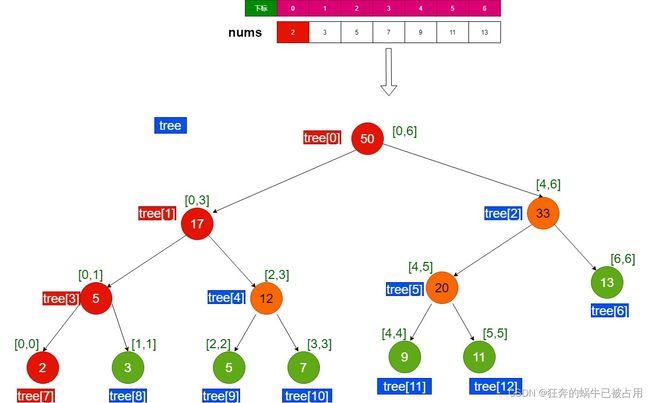
修改nums[0]=2;

我们看上图，修改nums[0],会影响到树的4节点；在我们修改nums数据之后，该如何找到在tree中有哪些节点被影响到了呢？
我们知道tree的叶子节点只存储了nums数组的一个元素值，因此只需要从tree的根节点（tree[0]）开始递归的找到这个叶子节点，修改值,并且重新计算这条递归路径上节点的值：tree[parent] = tree[leftNode] + tree[rightNode];

public void updateTree(int[] nums,int[] tree,int node,int start,int end,int index,int val){
	if(start == end){//区间只有一个值，是tree的叶子节点；
		tree[node] = val;
		nums[index] = val;
		return;
	}
	int mid = (start + end)/2;
	int leftNode  =  2 * node + 1;
	int rightNode =  2 * node + 2;
	if(index <= mid){//判断index在哪个半区;
		updateTree(nums,tree,leftNode ,start,mid,index,val);
	}else{
		updateTree(nums,tree,rightNode,mid+1,end,index,val);
	}	
	tree[node] = tree[leftNode] + tree[rightNode];//重新计算父节点的值；
}

查询nums数组任意区间的值

查询区间和线段树构造的区间，有3种关系：

• 1.查询区间完全包含了tree[node]区间；
• 2.查询区间与tree[node]的区间完全分离（没有重合部分）；
• 3.tree[node]区间大于查询区间或者与查询区间有部分重叠；

递归的查询区间的值，将查询区间包含tree[node]的值区间的所有tree[node]叠加返回；

1.当查询区间完全包含tree[node]的值区间时直接返回该区间的值；
2.当查询区间与tree[node]的值区间完全没有重合部分，则返回0；
3.当tree[node]的对应nums的值区间大于查询区间或者与查询区间有部分重叠，则分别递归查询分布在tree[node]左右两侧的值；左区间：[start,(start+end)/2]，右区间[(start+end)/2+1,end]

例子，查询区间：【1，5】;由于在二叉树中，并没有节点直接存储了这个查询范围的值；我们如何找出查询范围【1，5】的值呢？

1. 首先找到tree[0],我们通过[start,end] 知道tree[0] 是nums数组下标从0到6的元素之和，我们的查询范围是：1到5；查询范围包含在tree[0]中，因此分别查询 tree[0]的左右子节点；查询范围的【1，5】的值分布在tree[0]左右两边；
   res[1,5] = left [1,3] + right[4,5];
   通过递归找到结果：res[1,5] = tree[8] + tree[4] + tree[5];

//[l,r] ---> 查询区间
//[start,end] ---->tree[node]的值区间
public int sumTree(int[]nums,int[]tree,int node,int start,int end,int l,int r){

	if(r < start || l > end)return 0;//区间不在查询范围内
	else if(l <= start && end <= r)return tree[node];//tree[node]的区间完全包含在查询区间
	else{//[l,r]在start,end内；或者有重合部分
		int mid = (start + end)/2;
		int leftNode  = 2 * node + 1 ;
		int rightNode = 2 * node + 2 ;
		int leftVal  = sumTree(nums,tree,leftNode ,start,mid,l,r);
		int rightVal = sumTree(nums,tree,rightNode,mid+1,end,l,r);
		return leftVal + rightVal;
	}


}