二叉树的树状打印(Java)
原理部分
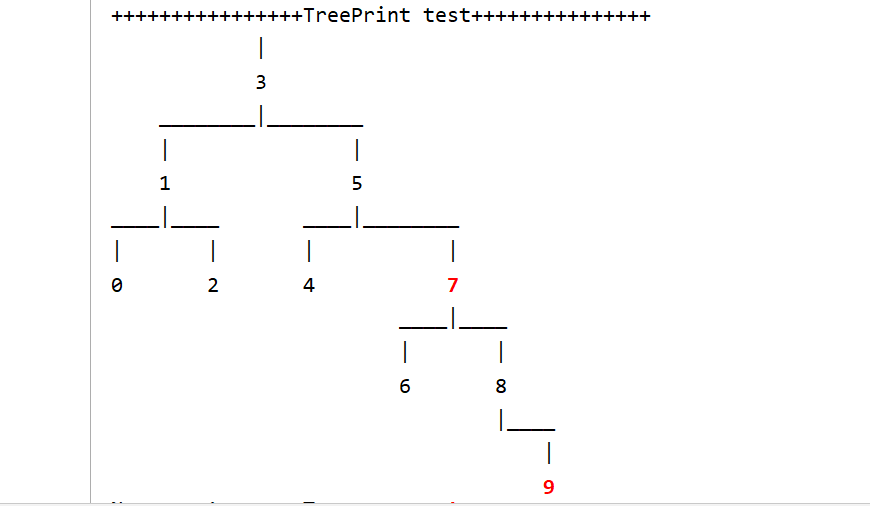
实现效果如下:
在控制台打印时,是从上往下一行一行打印的;上面的效果图是将二叉树一层的节点在同一行中打印,因此在遍历时应该层序遍历:将同一层的节点按顺序遍历打印,再继续遍历下一层的节点;
在打印同一层的节点时,要计算好每个节点之间的间隔距离,同一层节点之间的间隔可以看节点之间的横坐标之差;要计算出横坐标之差,就要得到每一个节点的横坐标;

如果按照: XA —> XG 的顺序将节点存储到数组中,那么每个节点对应的数组下标可以看作是节点的横坐标;在二叉树中,中序遍历的结果恰好是这个顺序;
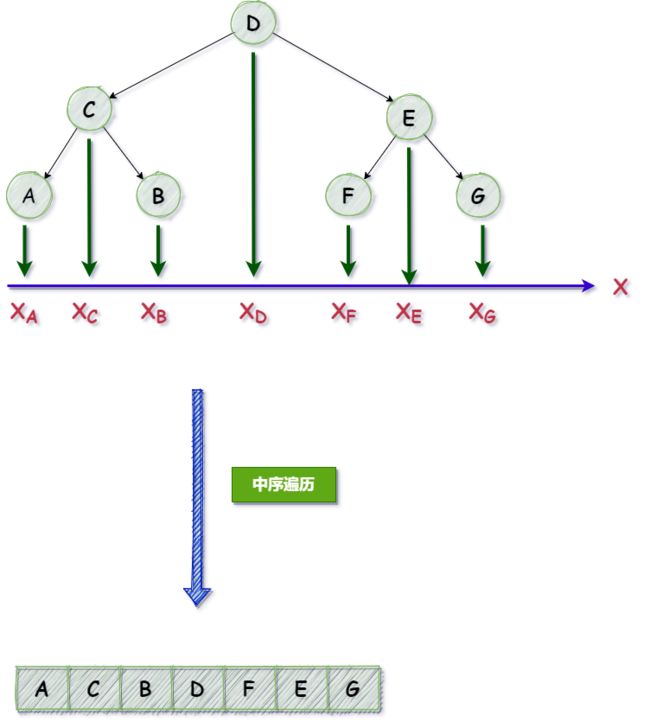
在打印完节点之后,还要打印链接子节点的线段;同一层节点之间有多个节点,因此会有多条链接子节点的线段;而这些线段也在同一层中,因此也要将这些线段拼接在一行中一起打印;
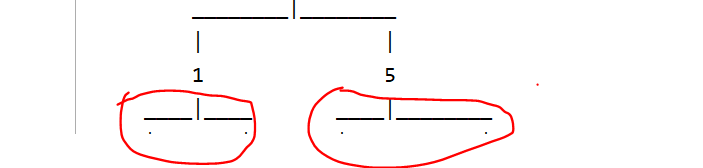
每一条链接子节点线段的长度如何确定呢?也很简单,子节点的坐标与当前节点坐标 之差就是线段的长度;因为节点可能会缺失左节点或者右节点,因此要分别计算链接左右子节点的线段长度;
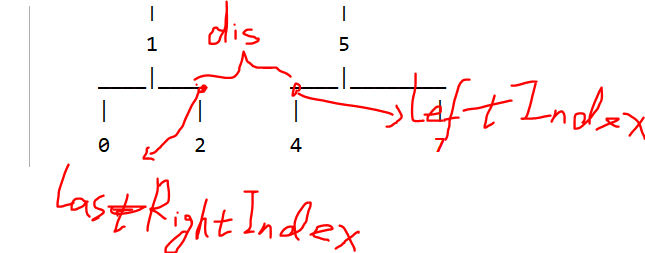
多条线段之间的间隔也要计算出来,这个就比较简单了两条线段之间的间隔: distance = leftIndex - lastRightIndex;
以上图为例,如果节点1没有right节点,那么lastRightIndex = 节点1的坐标;如果节点5没有left节点,那么leftIndex = 节点5的坐标 ;
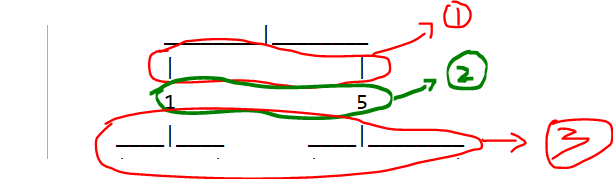
- 第一部分是数据节点上的竖线;
- 第二部分是,数据打印
- 第三部分是连接线;
代码
- 中序遍历,找到每个节点的坐标;
List<Node> mid = new ArrayList<>();
void midOrder(Node node){
if(node == null)return;
midOrder(node.left);
mid.add(node);
midOrder(node.right);
}
//将node ,index ====> 存入map中
Map<Node,Integer> map =new HashMap<>();
void init(){
if(root == null)return;
midOrder(root);
for (int i = 0; i < mid.size(); i++) {
map.put(mid.get(i),i);
}
}
- 层序遍历打印
void treePrint(List<Node> nodes){
if(nodes.isEmpty())return;
// nodes : 同一层节点
printLevel(nodes);//打印同一层的节点
List<Node> children = new ArrayList<>();
//顺序遍历下一层节点;
for (Node node : nodes) {
if(node.left != null)children.add(node.left);
if(node.right != null) children.add(node.right);
}
treePrint(children);//递归打印下一层节点
}
- 打印同一层节点
void printLevel(List<Node> nodes){
String VLine = "";
String dataLine = "";
String line = "";
int lastNodeIndex = 0;
int lastRightIndex = 0;
for (Node node : nodes) {
int x = map.get(node);
String addEmpty = getEmpty(x-lastNodeIndex);
lastNodeIndex = x;
VLine += addEmpty+"|";//竖线拼接
//数字拼接
dataLine += addEmpty+node.data;
//红黑树可以用下面打印语句,打印红色;
//if(node.red)
// dataLine+= addEmpty +"\033[91;1m"+node.data+"\033[0m";//打印红色
//else
// dataLine += addEmpty+node.data;
//======================组装,左右连接线=======================================
Node left = node.left;
Node right = node.right;
String leftLine = null;
String rightLine = null;
int leftIndex = -1;
int rightIndex = -1;
if(left != null){
leftIndex = map.get(left);
leftLine = getLineToSon(x - leftIndex);
}
if(right != null){
rightIndex = map.get(right);
rightLine = getLineToSon(rightIndex - x);
}
String curLine = (leftLine == null ? "" :leftLine) + "|"+(rightLine == null ? "" : rightLine);
if(leftLine == null && rightLine == null)curLine="";
//线段之间的间隔
int dif = (leftIndex == -1 ? x : leftIndex) - lastRightIndex;
String difEmpty = getEmpty(dif);
line += difEmpty + curLine;//拼接线段
lastRightIndex = rightIndex == -1 ? x : rightIndex;
}
System.out.println(VLine +"\n" + dataLine +"\n" + line);
}
String getEmpty(int x){
String empty ="";
for (int i = 0; i < x; i++) {
empty+="\t";
}
return empty;
}
//链接子线段的长度
String getLineToSon(int end){
String line = "";
if(end ==0)return line;
for (int i = 0; i < end; i++) {
line+="____";
}
return line;
}
- 打印测试
public void treePrint(){
init();
List<Node> nodes = new ArrayList<>();
nodes.add(root);
treePrint(nodes);
}
@Test
public void test(){
for (int i = 0; i < 20; i++) {
addVal(i);
}
System.out.println("\n++++++++++++++++TreePrint test+++++++++++++++");
treePrint();
}
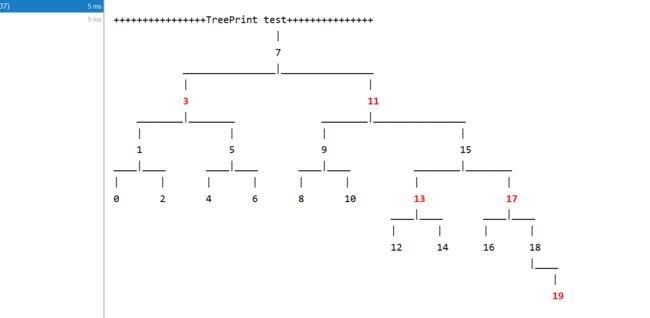
- 结果
红黑树和打印测试代码:Gitee
优化
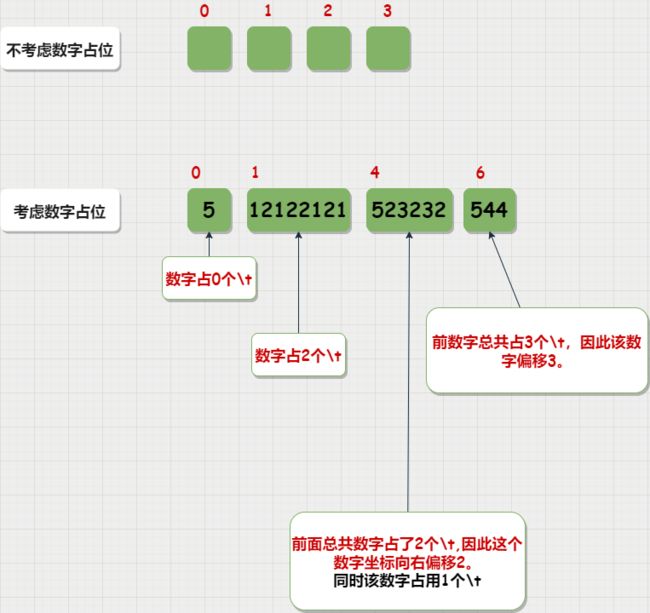
上面的计算过程中没有考虑到数字占用的位置,因此在数字很大的时候打印就会出错;节点之间的单位空格距离是\t,而一个\t等于4个_长度,但这个长度不是固定的;如果:数字 + \t,数字长度小于4,那么\t的长度就等于:4-numberLength;也就是说,数字长度小于4时与\t一起使用是不占用位置的;
比如:12+\t,效果等于12+2个_<—> 12__,还是一个\t的长度;如果数字长度大于4,比如12345+\t中这个\t占用3个_长度,总长度8个_,那么占用长度相当于2个\t;数字占用\t个数可以用:numberLength/4来计算;
考虑到了数字占位,那么每个数字的下标也要重新计算了。每个数字之间的距离仍然是\t,但是每个数字还要占位置因此当数字占位之后,后续的数字的坐标都要改;
计算坐标代码:
void init(){
if(root == null)return;
midOrder(root);
int offset=0;//计算偏移量
for (int i = 0; i < mid.size(); i++) {
map.put(mid.get(i),i+offset);
offset+=numberLength(mid.get(i));//numberLength计算数字占用\t
}
}
int numberLength(Node node){
if(node == null)return 0;
int value = node.data;
int count=1;
while((value/=10)>0){
count++;
}
return count/4;
}
数字拼接代码:
void printLevel(List<Node> nodes){
String VLine = "";
String dataLine = "";
String line = "";
int lastNodeIndex = 0;
int lastRightIndex = 0;
//上一个节点,是用来获取上一个数字占用了多少个\t
Node lastNode = null;
for (Node node : nodes) {
int x = map.get(node);
String addEmpty = getEmpty(x-lastNodeIndex);
VLine += addEmpty+"|";//竖线拼接
===========================改动部分 start====================================================================
//数字拼接,重新计算2个数字的间隔,要减去上一个数字占用的位置;
String numberEmpty = getEmpty(x-lastNodeIndex-numberLength(lastNode));
dataLine += numberEmpty+node.data;
//if(node.red)
// dataLine+= numberEmpty +"\033[91;1m"+node.data+"\033[0m";//打印红色
//else
// dataLine += numberEmpty+node.data;
===========================改动部分 end======================================================================
Node left = node.left;
Node right = node.right;
String leftLine = null;
String rightLine = null;
int leftIndex = -1;
int rightIndex = -1;
if(left != null){
leftIndex = map.get(left);
leftLine = getLineToSon(x - leftIndex);
}
if(right != null){
rightIndex = map.get(right);
rightLine = getLineToSon(rightIndex - x);
}
String curLine = (leftLine == null ? "" :leftLine) + "|"+(rightLine == null ? "" : rightLine);
if(leftLine == null && rightLine == null)curLine="";
//线段之间的间隔
int dif = (leftIndex == -1 ? x : leftIndex) - lastRightIndex;
String difEmpty = getEmpty(dif);
line += difEmpty + curLine;//拼接线段
lastRightIndex = rightIndex == -1 ? x : rightIndex;
lastNode = node;
lastNodeIndex = x;
}
System.out.println(VLine +"\n" + dataLine +"\n" + line);
}
其余部分不变;
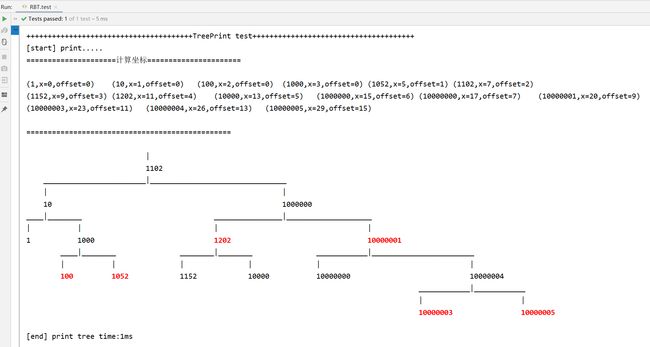
测试:
@Test
public void test(){
for (int i = 1052; i < 1240; i+=50) {
addVal(i);
}
addVal(1);//占0个\t
addVal(10);
addVal(100);
addVal(1000);//占1个\t
addVal(10000);
addVal(1000000);
addVal(10000000);//占2个\t
addVal(10000001);
addVal(10000003);
addVal(10000004);
addVal(10000005);
System.out.println("\n+++++++++++++++++++++++++++++++++++++++TreePrint test++++++++++++++++++++++++++++++++++++++");
System.out.println("[start] print.....");
long start = System.currentTimeMillis();
treePrint();
long end = System.currentTimeMillis();
System.out.println("[end] print tree time:"+(end-start)+"ms");
}
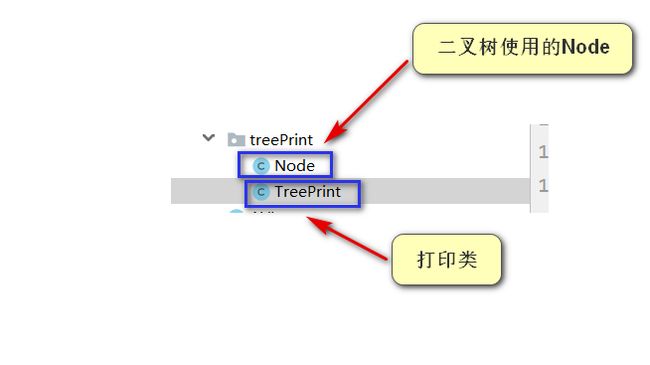
打印类
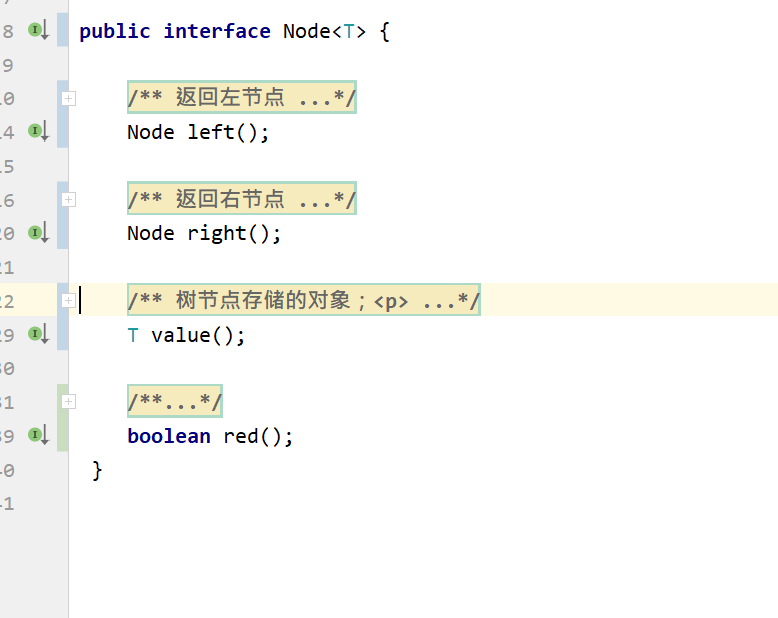
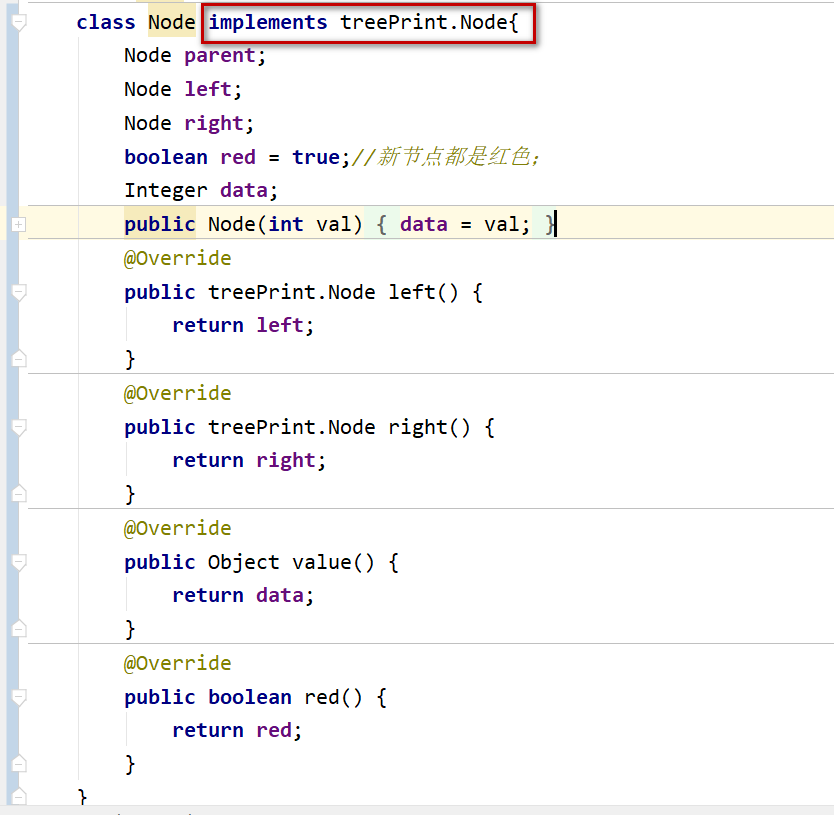
(PS:上面的代码都是根据这篇博客直接写的,过程没有封装。如果看上面的代码觉得比较混乱,可以看下面gitee地址的代码。)为了方便测试所有的二叉树抽象出了共用的节点类Node,打印类:TreePrint。所有二叉树使用的节点类Node 只要实现treePrint.Node接口都可以用TreePrint类打印;在使用TreePrint时只需要将自己要测试的二叉树生成的root节点注入到TreePrint对象中就可以使用TreePrint打印了;
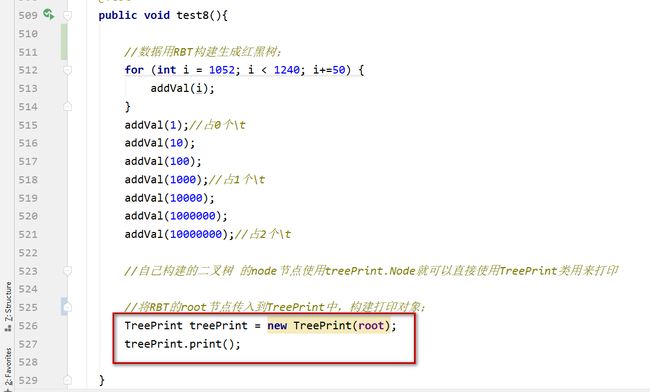
使用RBT测试:
- 1.RBT的Node实现treePrint.Node
- 2.使用TreePrint对象打印
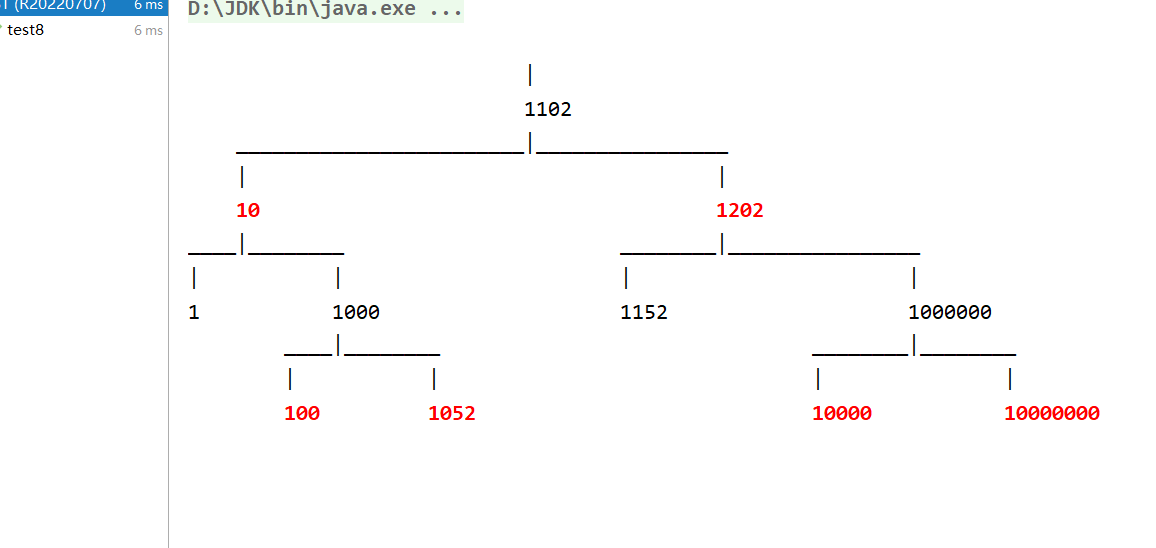
结果:
代码地址TreePrint