pytorch学习笔记2-线性模型

一维线性回归

例1 随机设置点回归

# 引入numpy
import numpy as np

# 随机设置数据
x_train = np.array([[3.3], [4.4], [5.5], [6.71], [6.93], [4.168], [9.779], [6.182], [7.59], [2.167], [7.042], [10.791], [5.313], [7.997], [3.1]], dtype = np.float32)
y_train = np.array([[1.7], [2.76], [2.09], [3.19], [1.694], [1.573], [3.366], [2.596], [2.53], [1.221], [2.827], [3.465], [1.65], [2.904], [1.3]], dtype = np.float32)

# 引入matplotlib，用来画图，下面两句常用
import matplotlib as mpl
import matplotlib.pyplot as plt

# 绘制散点图
plt.scatter(x_train, y_train)
plt.show()

番外：
matplotlib的使用

# 将 numpy.array 转换成Tensor
import torch
x_train = torch.from_numpy(x_train)
y_train = torch.from_numpy(y_train)

# 定义一个简单模型
import torch.nn as nn # 不能丢
class LinearRegression(nn.Module):
    def __init__(self):
        super(LinearRegression, self).__init__()
        self.linear = nn.Linear(1, 1)# 输入输出都是1维的
    
    def forward(self, x):
        out = self.linear(x)
        return out
    
if torch.cuda.is_available():
    model = LinearRegression().cuda()
else:
    model = LinearRegression()

# 这段有ERROR，后面有解决方法
from torch.autograd import Variable
# 训练模型
num_epochs = 1000
for epoch in range(num_epochs):
    if torch.cuda.is_available():
        inputs = Variable(x_train).cuda()
        target = Variable(y_train).cuda()
    else:
        inputs = Variable(x_train)
        target = Variable(y_train)
    
    # forward
    out = model(inputs)
    loss = criterion(out, target)
    # backward
    optimizer.zero_grad() # 归零梯度
    loss.backward() # 反向传播
    optimizer.step() # 更新参数
    
    if (epoch + 1) % 20 == 0:
        print('Epoch[{}/{}],loss: {:.6f}'.format(epoch+1, num_epochs, loss.data[0]))

ERROR

21行：
IndexError: invalid index of a 0-dim tensor. Use `tensor.item()` in Python or `tensor.item()` in C++ to convert a 0-dim tensor to a number

解决方法：
将 21行 loss.data[0] 改为 loss.item()

更改后代码如下：

# 这回对了，不报错了
from torch.autograd import Variable
# 训练模型
num_epochs = 1000
for epoch in range(num_epochs):
    if torch.cuda.is_available():
        inputs = Variable(x_train).cuda()
        target = Variable(y_train).cuda()
    else:
        inputs = Variable(x_train)
        target = Variable(y_train)
    
    # forward
    out = model(inputs)
    loss = criterion(out, target)
    # backward
    optimizer.zero_grad() # 归零梯度
    loss.backward() # 反向传播
    optimizer.step() # 更新参数
    
    if (epoch + 1) % 20 == 0:
        print('Epoch[{}/{}],loss: {:.6f}'.format(epoch+1, num_epochs, loss.item()))

Epoch[20/1000],loss: 0.169452
Epoch[40/1000],loss: 0.169436
Epoch[60/1000],loss: 0.169431
Epoch[80/1000],loss: 0.169426
Epoch[100/1000],loss: 0.169420
Epoch[120/1000],loss: 0.169415
Epoch[140/1000],loss: 0.169410
Epoch[160/1000],loss: 0.169405
Epoch[180/1000],loss: 0.169400
Epoch[200/1000],loss: 0.169395
Epoch[220/1000],loss: 0.169390
Epoch[240/1000],loss: 0.169385
Epoch[260/1000],loss: 0.169380
Epoch[280/1000],loss: 0.169376
Epoch[300/1000],loss: 0.169371
Epoch[320/1000],loss: 0.169366
Epoch[340/1000],loss: 0.169362
Epoch[360/1000],loss: 0.169357
Epoch[380/1000],loss: 0.169353
Epoch[400/1000],loss: 0.169348
Epoch[420/1000],loss: 0.169344
Epoch[440/1000],loss: 0.169339
Epoch[460/1000],loss: 0.169335
Epoch[480/1000],loss: 0.169331
Epoch[500/1000],loss: 0.169326
Epoch[520/1000],loss: 0.169322
Epoch[540/1000],loss: 0.169318
Epoch[560/1000],loss: 0.169314
Epoch[580/1000],loss: 0.169310
Epoch[600/1000],loss: 0.169306
Epoch[620/1000],loss: 0.169302
Epoch[640/1000],loss: 0.169298
Epoch[660/1000],loss: 0.169294
Epoch[680/1000],loss: 0.169290
Epoch[700/1000],loss: 0.169286
Epoch[720/1000],loss: 0.169283
Epoch[740/1000],loss: 0.169279
Epoch[760/1000],loss: 0.169275
Epoch[780/1000],loss: 0.169271
Epoch[800/1000],loss: 0.169268
Epoch[820/1000],loss: 0.169264
Epoch[840/1000],loss: 0.169261
Epoch[860/1000],loss: 0.169257
Epoch[880/1000],loss: 0.169254
Epoch[900/1000],loss: 0.169250
Epoch[920/1000],loss: 0.169247
Epoch[940/1000],loss: 0.169243
Epoch[960/1000],loss: 0.169240
Epoch[980/1000],loss: 0.169237
Epoch[1000/1000],loss: 0.169233

# 预测结果
model.eval() # 将模型变成测试模式
predict = model(Variable(x_train))
predict = predict.data.numpy()
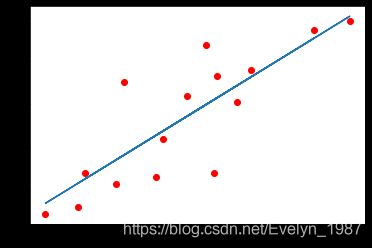
plt.plot(x_train.numpy(), y_train.numpy(), 'ro', label = 'Original Data')
plt.plot(x_train.numpy(), predict, label = 'Fitting Line')
plt.show()

注意：
model.eval() 将模型变为测试模式，因为有一些层操作，比如Dropout和BatchNormalization在训练和测试的时候是不一样的，所以需要通过这样一个操作来转换这些不一样的层操作。

多项式回归

例2 3次多项式回归

import torch
# 使用torch.cat（）实现Tensor的拼接
def make_features(x):
    x = x.unsqueeze(1)
    return torch.cat([x ** i for i in range(1, 4)], 1)

将输入的数据扩展成矩阵形式

# unsqueeze(1)将原来的Tensor大小由3变成（3,1）
W_target = torch.FloatTensor([0.5, 3, 2.4]).unsqueeze(1)
b_target = torch.FloatTensor([0.9])

# x.mm（W_target）表示做矩阵乘法
def f(x):
    return x.mm(W_target) + b_target[0]

#采样点，随机生成一些数得到每次的训练集：
def get_batch(batch_size = 32):
    random = torch.randn(batch_size)
    x = make_features(random)
    y = f(x)
    if torch.cuda.is_available():
        return Variable(x).cuda(), Variable(y).cuda()
    else:
        return Variable(x), Variable(y)

#定义多项式模型
import torch.nn as nn
class poly_model(nn.Module):
    def __init__(self):
        super(poly_model, self).__init__()
        self.poly = nn.Linear(3, 1)
    
    def forward(self, x):
        out = self.poly(x)
        return out
    
if torch.cuda.is_available():
    model = poly_model().cuda()
else:
    model = poly_model()

import torch.optim as optim
# 定义损失函数和优化器
criterion = nn.MSELoss()
optimizer = optim.SGD(model.parameters(), lr=1e-3)

# 训练模型
epoch = 0
while True:
    # 获取数据
    batch_x, batch_y = get_batch()
    # 前向传递
    output = model(batch_x)
    loss = criterion(output, batch_y)
    print_loss = loss.item()
    # 重置梯度
    optimizer.zero_grad()
    # 后向传递
    loss.backward()
    # 更新参数
    optimizer.step()
    epoch += 1
    # 均方误差小于0.001时，停止优化
    if print_loss < 1e-3:
        break

参考资料

《深度学习入门之PyTorch》 廖星宇 编著