线性代数拾遗（5） —— 矩阵的四个基本子空间

• 参考：麻省理工线性代数
• 本文介绍矩阵的四个基本子空间 —— 列空间、行空间、零空间、左零空间

---

1. 线性空间（向量空间）、子空间

• 这部分内容国内线性代数课似乎不会深入讲，简单补充一下

  1. 给定一些元素构成集合，在集合上定义一些运算，再定义运算规则，我们就得到了一个代数系统
  2. 数域是一个代数系统，它的集合中都是各种数（实数、复数、无理数…），要求必须包含0和1，定义数的四则运算，且要求关于这些运算封闭
  3. 在数域的基础上，再给定一些元素（向量、矩阵、函数…什么都行），定义 加法 和 数乘 两个运算，当两个运算满足封闭性和八条性质时，称为一个线性空间
  4. 线性空间中允许元素间线性表示，这样就有了基和坐标向量的概念，而坐标向量是一个数组成的向量，因此线性空间中任意元素都可以一一对应到某个数的向量，所以线性空间也称为向量空间
  5. 线性空间/向量空间的基础上，增加一个元素的內积运算，定义相应的运算规则，得到內积空间
  6. 线性空间的元素的非空子集，满足加法和数乘运算的封闭性及八条性质，称为线性子空间（事实上只要满足封闭性，其他性质自动满足）

  这部分内容详见

  1. 双语矩阵论课程笔记（2）—— 【chapter 1】 Vector Spaces (Linear Spaces)
  2. 双语矩阵论课程笔记（3）—— 【chapter 2】 Inner Product Spaces

2. 矩阵的四个基本子空间

• 给定秩为 $r$ 的矩阵 ${A\text{A}A}_{m\times n}$，本章介绍以下四个重要子空间

  子空间	说明	向量尺寸	维数	求基
  列空间 $C(A\text{A}A)$	${A\text{A}A}_{m\times n}$ 所有列的线性组合构成	${\mathbb{R}}^m$	$r$	列化阶梯型
  行空间 $C(A^{\top }\text{A⊤}{A}^{\top })$	${A\text{A}A}_{m\times n}$ 所有行的线性组合构成	${\mathbb{R}}^n$	$r$	行化阶梯型
  零空间 $N(A\text{A}A)$	$Ax\text{Ax}Ax=0\text{0}0$ 的解空间	${\mathbb{R}}^n$	$n-r$	求基础解析
  左零空间 $N({A\text{A}A}^{\top })$	$y^{\top }A\text{y⊤A}{y}^{\top }A=0^{\top }\text{0⊤}{0}^{\top }$ 的解空间	${\mathbb{R}}^m$	$m-r$	类似化阶梯型求逆

2.1 列空间

• 给定秩为 $r$ 的矩阵 ${A\text{A}A}_{m\times n}$，列空间是由 $A\text{A}A=[{a\text{a}a}_1,{a\text{a}a}_2,...,{a\text{a}a}_n]$ 所有列向量的线性组合构成的空间，记为 $$C(A\text{A}A)=\text{span}({a\text{a}a}_1,{a\text{a}a}_2,...,{a\text{a}a}_n)$$
• 基本性质
  1. 尺寸：空间中所有元素尺寸同 $A\text{A}A$ 列向量尺寸 $m\times 1$，即 $C(A\text{A}A)\in {\mathbb{R}}^m$
  2. 维数：矩阵的秩定义为非零的子式（任取 $k$ 行 $k$ 列构成的行列式）的最大阶数，也就是最大的线性无关行列向量个数，因此矩阵列空间的维数和矩阵的秩相等，即 $\dim C(A\text{A}A)=r$
  3. 基：列空间的基，只要在所有列向量中找 $r$ 个线性无关的就行了，注意到做列初等变换其实就是在对列做各种线性组合操作，变换后的矩阵列空间不变（当然，这时行空间就改变了），故可以通过列初等变换化竖直阶梯型的方式找出一组基

2.2 零空间

• 给定秩为 $r$ 的矩阵 ${A\text{A}A}_{m\times n}$，零空间是由 $Ax\text{Ax}Ax=0\text{0}0$ 的所有解向量 ${x\text{x}x}_i$ 的线性组合构成的空间，也就是这个 $n$ 元齐次线性方程组的解空间，记为 $N(A\text{A}A)$
• 基本性质
  1. 尺寸：空间中所有元素尺寸同 $Ax\text{Ax}Ax=0\text{0}0$ 的解 ${x\text{x}x}_{n\times 1}$ 的尺寸 $n\times 1$，即 $C(A\text{A}A)\in {\mathbb{R}}^n$
  2. 维数：根据性质：n 元齐次线性方程组解空间的维数，加上此方程组系数矩阵的秩 r，等于未知量个数 n，有 $\dim N(A\text{A}A)=n-r$
  3. 基：就是求齐次线性方程组基础解系，做初等行变换化阶梯型来找通解

     这里可以用张宇老师的方法，化阶梯形后，得到 $A\text{A}A$ 的秩 $r$，然后得到零空间的维数 $n-r$，待定系数先写出基向量组形式，再把阶梯矩阵中每个阶梯划去一列，剩下的列的位置对应到基向量组上，在这个位置用单位阵填充，以保证各个基向量线性无关，最后带入有限方程解出其余系数

• 从几何角度，零空间可以理解为被矩阵 $A\text{A}A$ 变化后压缩到原点的空间

2.3 行空间

• 给定秩为 $r$ 的矩阵 ${A\text{A}A}_{m\times n}$，行空间是由 $A\text{A}A=[{a\text{a}a}_1^{\top },{a\text{a}a}_2^{\top },...,{a\text{a}a}_m^{\top }{]}^{\top }$ 所有行向量的线性组合构成的空间，注意到这其实就是 $A^{\top }\text{A⊤}{A}^{\top }$ 的列空间，所以直接记为
  $$C(A^{\top }\text{A⊤}{A}^{\top })=\text{span}({a\text{a}a}_1^{\top },{a\text{a}a}_2^{\top },...,{a\text{a}a}_m^{\top })$$
• 基本性质
  1. 尺寸：空间中所有元素尺寸同 $A\text{A}A$ 行向量尺寸 $n\times 1$，即 $C(A\text{A}A)\in {\mathbb{R}}^n$
  2. 维数：同2.1节分析，矩阵行空间维数和矩阵的秩相等，即 $\dim C(A^{\top }\text{A⊤}{A}^{\top })=r$
  3. 基：同2.1节分析，通过行初等变换化阶梯型的方式找出一组基

2.4 左零空间

• 给定秩为 $r$ 的矩阵 ${A\text{A}A}_{m\times n}$，左零空间是由 $y^{\top }A\text{y⊤A}{y}^{\top }A=0^{\top }\text{0⊤}{0}^{\top }$ 的所有解向量 $y_i^{\top }\text{yi⊤}{y}_i^{\top }$的线性组合构成的空间。注意到这是个行向量空间，而我们通常统一用列向量来表示向量，因此对齐次线性方程两边取转置，得到 $A^{\top }y\text{A⊤y}{A}^{\top }y=0\text{0}0$，可见 $A\text{A}A$ 的左零空间其实就是 $A^{\top }\text{A⊤}{A}^{\top }$ 的（列向量）的零空间，所以直接记为 $N(A^{\top }\text{A⊤}{A}^{\top })$
• 基本性质
  1. 尺寸：空间中所有元素尺寸同 $y^{\top }\text{y⊤}{y}^{\top }$ 列向量尺寸 $m\times 1$，即 $C(A\text{A}A)\in {\mathbb{R}}^m$
  2. 维数：矩阵的秩定义为非零的子式（任取 $k$ 行 $k$ 列构成的行列式）的最大阶数，也就是最大的线性无关行列向量个数，因此矩阵列空间的维数和矩阵的秩相等，即 $\dim C(A\text{A}A)=r$
  3. 基：这里求基时，我们使用类似化阶梯型求逆矩阵的方式，通过初等行变换进行以下操作
     $$\left[\begin{array}{cc}{A\text{A}A}_{m\times n}& {I\text{I}I}_{m\times m}\end{array}\right]\to \left[\begin{array}{cc}{R\text{R}R}_{m\times n}& {K\text{K}K}_{m\times m}\end{array}\right]$$ 其中 $I\text{I}I$ 是 $m$ 阶单位阵。事实上，上面这个变换就是通过左乘 ${K\text{K}K}_{m\times m}$ 来进行的，即
     $${K\text{K}K}_{m\times m}\left[\begin{array}{cc}{A\text{A}A}_{m\times n}& {I\text{I}I}_{m\times m}\end{array}\right]=\left[\begin{array}{cc}{R\text{R}R}_{m\times n}& {K\text{K}K}_{m\times m}\end{array}\right]$$ 可见有
     $${K\text{K}K}_{m\times m}{A\text{A}A}_{m\times n}={R\text{R}R}_{m\times n}$$ 显然，令 ${R\text{R}R}_{m\times n}={I\text{I}I}_{m\times n}$，就有 ${A\text{A}A}^{-1}={K\text{K}K}_{m\times m}$，这是我们都学过的求逆方法。现在假设我们使 ${R\text{R}R}_{m\times n}$ 变化为正规矩阵，即
     $${R\text{R}R}_{m\times n}=\left[\begin{array}{ccc}& {I\text{I}I}_{r\times r}& {F\text{F}F}_{r\times n-r}\\ & {0\text{0}0}_{m-r\times r}& {0\text{0}0}_{m-r\times n-r}\end{array}\right]$$ 左上角是 $r$ 阶单位阵，右上角是任意矩阵，下面是全零行。这时再考虑
     $${K\text{K}K}_{m\times m}{A\text{A}A}_{m\times n}={R\text{R}R}_{m\times n}$$ 记住我们要找左零空间，也就是要找 ${K\text{K}K}_{m\times m}$ 中的那些右乘 ${A\text{A}A}_{m\times n}$ 后变为零向量的行向量，注意到这些变换结果恰好记录在 ${R\text{R}R}_{m\times n}$ 对应的行向量中，因此，我们只要先求出 ${K\text{K}K}_{m\times m}$，再取其最下面 $m-r$ 个行向量即得到 $A\text{A}A$ 左零空间的一组基。至于 ${K\text{K}K}_{m\times m}$ 的求法，只要记住将 ${A\text{A}A}_{m\times n}$ 通过初等行变换化为 ${R\text{R}R}_{m\times n}$ 的过程，再对 ${I\text{I}I}_{m\times m}$ 做相同操作即可

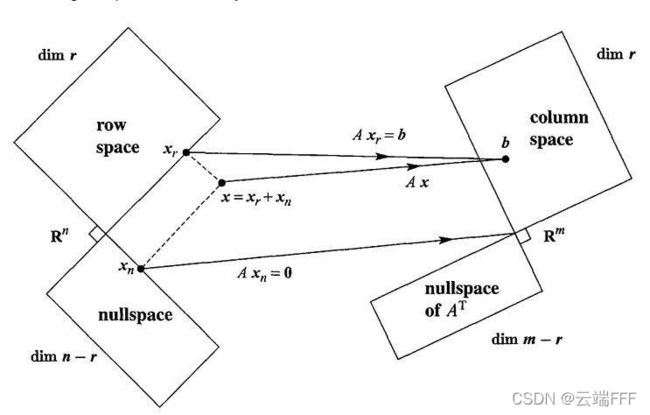
3. 子空间的正交关系

• 正交关系
  1. 两向量正交即两內积为0
  2. 一个向量空间和另一个向量空间正交，意味着一个空间中任意向量和另一空间中任意向量正交，即两组基正交
• 给定秩为 $r$ 的矩阵 ${A\text{A}A}_{m\times n}$，本章说明如下正交关系
  1. $r$ 维行空间 $C(A^{\top }\text{A⊤}{A}^{\top })$ 和 $n-r$ 维零空间 $N(A\text{A}A)$ 正交，二者是 $n$ 维空间的正交直和
  2. $r$ 维列空间 $C(A\text{A}A)$ 和 $m-r$ 维左零空间 $N(A^{\top }\text{A⊤}{A}^{\top })$ 正交，二者是 $m$ 维空间的正交直和

3.1 证明

• 先证明行空间 $C(A^{\top }\text{A⊤}{A}^{\top })$ 和零空间 $N(A\text{A}A)$ 正交：从零空间 $N(A\text{A}A)$ 定义入手，它是 $Ax=0\text{Ax=0}Ax=0$ 的解空间，即
  $$\left[\begin{array}{c}{a_1\text{a1}{a}_1}^{\top }\\ {a_2\text{a2}{a}_2}^{\top }\\ ⋮\\ {a_m\text{am}{a}_m}^{\top }\end{array}\right]x\text{x}x=\left[\begin{array}{c}0\text{0}0\\ 0\text{0}0\\ ⋮\\ 0\text{0}0\end{array}\right]$$ 可见 $A\text{A}A$ 中任意行向量 ${a_i\text{ai}{a}_i}^{\top }$，和 $N(A\text{A}A)$ 中任意列向量 $x\text{x}x$ 做內积都为 $0\text{0}0$，显然两空间中任意向量的线性组合也正交，因此两空间正交
• 根据矩阵转置等价性质，$C(A^{\top }\text{A⊤}{A}^{\top })$ 和 $N(A\text{A}A)$ 正交 $\Rightarrow$ 列空间 $C(A\text{A}A)$ 和左零空间 $N(A^{\top }\text{A⊤}{A}^{\top })$ 正交
• 再根据维度关系，$C(A^{\top }\text{A⊤}{A}^{\top })$ 和 $N(A\text{A}A)$ 是 $n$ 维空间的正交直和；$C(A\text{A}A)$ 和 $N(A^{\top }\text{A⊤}{A}^{\top })$ 是 $m$ 维空间的正交直和

3.2 小结

• 最后用一张图总结本文