DeepGCNs- Can GCNs Go as Deep as CNNs?
本篇文章主要阐述了我们怎么去构建一个网络使得GCN能够堆叠更深的层且不会发生梯度消失的问题。讲了3个method:1.Resnet 2.Densenet 3.Dilated convolutions 。
该模型的很多技巧以及method对其他的方向感觉有比较大的借鉴意义。
Introduction
在目前我们所用到的GCN中,一般layers都大致在4层左右,并不会堆叠更多,主要是因为随着层数的增加,会出现梯度消失,反向传播over-smoothing等问题。
要解决这个问题我们主要提出了三个方法:Resnet,DenseNet,Dilated. conv。其中Resnet,DenseNet就是引荐于CNN。但是因为层数的堆叠会因为池化导致空间信息的损失,而扩展卷积(Dilated conv)则可以尽量减少空间信息的损失。
本文就是以这三种方法为基础,构建一个在GCN中也能使用的模型。
文章思路启发:在早期CNN刚提出的时候,也出现过因为层数过低以及局部感受野得到信息受限等问题,我们可以以CNN为启发,对GCN进行改进。
Methodology
Graph Definition
我们定义一个图 G = ( V , E ) G=(V,E) G=(V,E),其中 V V V表示该图的结点的集合, E E E表示为 ( e i , e j ) (e_i,e_j) (ei,ej),即结点i与j有边。
Graph Convolution Networks
与CNN一样,在图网络中,我们同样是对邻边的结点信息做一个权重聚合,然后来更新中心结点。我们可以定义图 G l G_{l} Gl的特征矩阵为所有节点在 l l l层时的特征向量的拼接,图的特征可以表达为: h g = [ h v 1 , h v 2 , h v 3 , … , h v N ] T ∈ R N ∗ D h_g=[h_{v1},h_{v2},h_{v3},…,h_{vN}]^T \in R^{N*D} hg=[hv1,hv2,hv3,…,hvN]T∈RN∗D其中D表示特征向量的维度。
在第l层上,我们的图卷积可以用下面的公式定义:
G l + 1 = F ( G l , W l ) = U p d a t e ( A g g r e g a t e ( G l , W l a g g ) , W l u p d a t e ) G_{l+1}=F(G_l,W_l)=Update(Aggregate(G_l,W_l^{agg}),W_l^{update}) Gl+1=F(Gl,Wl)=Update(Aggregate(Gl,Wlagg),Wlupdate)
其中Update函数是对于输出层图的特征更新,更新函数的权重矩阵为 W l u p d a t e W_l^{update} Wlupdate, a g g r e g a t e aggregate aggregate函数是图中的每一个结点依据邻边信息的聚合,形成新的结点特征向量,其中聚合信息时的权重矩阵为 W l a g g W_l^{agg} Wlagg。在对每一个结点 v i v_i vi进行aggregate操作时,都是先对邻边结点特征进行update,再聚合到该结点 v i v_i vi上。
Dynamic Edges
目前大多数的研究工作都是基于固定的图,在每一次的迭代中去升级结点信息,但是缺忽略了边。
我们可以利用**边卷积(EdgeConv)**去选择最近的邻边来重构每一层的图。
在文章的模型中,我们使用了这样的边卷积方案,并且从实验可以得到结论:利用边卷积动态改变图结构可以有效的避免over-smoothing,并且可以有效的扩大感受野。
边卷积的方法:Dilated K-NN function。在下文中会详细讲到。
Residual Learning for GCN
我们定义一个函数 F ( ∗ ) F(*) F(∗)是将一个图做一个朴素的操作,得到一个新的图的表示。其次,我们定义一个残插学习框架如下:
G l + 1 = F ( G l , W l ) + G l = G l + 1 r e s + G l G_{l+1}=F(G_l,W_l)+G_l=G_{l+1}^{res}+G_l Gl+1=F(Gl,Wl)+Gl=Gl+1res+Gl
意思就是在朴素网络操作的基础上再加上一个l层网络的图特征。作者称之为ResGCN.
Dense Connections in GCNs
DenseNet是所有层之间的密集拼接,可以提高各层信息的流动,有效利用每个层得到的特征表示。在这里我们把它应用到GCN上。
在DenseGCN中,第l层的信息是l层输出信息与之前所有层的输出特征信息的拼接。利用公式我们可以定义为:
G l + 1 = H ( G l , W l ) = T ( F ( G l , W l ) , G l ) = T ( F ( G l , W l ) , . . . , F ( G 0 , W 0 ) , G 0 ) G_{l+1}=H(G_l,W_l)\\ =\Tau(F(G_l,W_l),G_l)\\ =\Tau(F(G_l,W_l),...,F(G_0,W_0),G_0) Gl+1=H(Gl,Wl)=T(F(Gl,Wl),Gl)=T(F(Gl,Wl),...,F(G0,W0),G0)
T \Tau T就是拼接操作,F是layer中由input得到output的操作。
Dilated Aggregation in GCNs
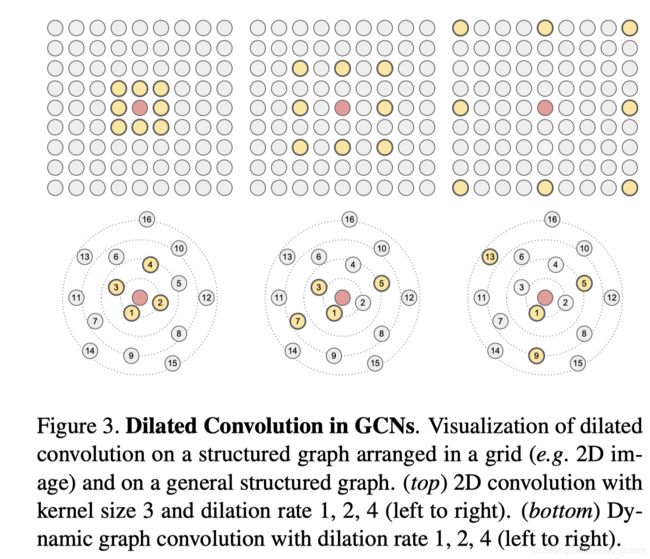
在CNN,利用实验表明了通过扩展卷积的方法我们可以聚合得到更多的信息,并且对于特征信息的损失很少。我们这里类似于CNN中扩展卷积的实现方法,利用k-NN去做图的邻边的扩展。
Detail:
对于一个输入图网络 G = ( V , E ) G=(V,E) G=(V,E),扩展系数为 d,在利用k-NN进行扩展卷积,我们将寻找距离中心结点 v v v最近的k*d个结点,利用集合表示为 ( u 1 , u 2 , … , u k d ) (u_1,u_2,…,u_{kd}) (u1,u2,…,ukd).这k *d个结点是距离v 结点最近的,我们从这些结点中选择出结点 ( u 1 , u 1 + d , u 1 + 2 d , … , u 1 + ( k − 1 ) d ) (u_1,u_{1+d},u_{1+2d},…,u_{1+(k-1)d}) (u1,u1+d,u1+2d,…,u1+(k−1)d).
则我们选择的d-dilated neighbors of vertex v 为:
N ( d ) ( v ) = { u 1 , u 1 + d , u 1 + 2 d , … , u 1 + ( k − 1 ) d } N^{(d)}(v)=\{u_1,u_{1+d},u_{1+2d},…,u_{1+(k-1)d} \} N(d)(v)={u1,u1+d,u1+2d,…,u1+(k−1)d}
这时我们就可以构造边 ( v , u i ∣ u i ∈ N ( d ) ( v ) ) (v,u_i |u_i \in N^{(d)}(v)) (v,ui∣ui∈N(d)(v)).,对于在该层我们新构造的边,再去做GCN aggregation 和update,以此得到每一个结点的feature h v ( d ) h_v^{(d)} hv(d).
Note:这里为了增加泛化性,在实际应用中作者用了随机扩展(stochastic convolution).
Network Architectures
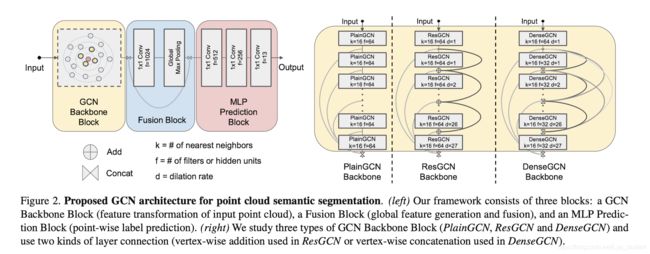
利用上述理论我们可以新构建GCN的框架如上图所示。主要分为三大部分:GCN backbone,fusion block,MLP prediction block.我们在设计模型时仅仅会改变GCN block部分。即会利用PlainGCN,ResGCN,DenseGCN,而GCN中的卷积也将使用本文所述的图上扩展卷积的方法。
具体的实现细节需要参考论文
Conclusion
本篇文章很好的介绍了加深图网络的方法,并且取得了很好的表现。但个人认为本篇文章中的边卷积中利用扩展卷积是一个很大的亮点,增大了局部感受野。后续工作会针对作者所提出的这些方法进行研究,应用到其他task上。