深度学习笔记（李宏毅）DataWhale八月组队
文章目录
- 机器学习介绍
- 回归
-
- 模型步骤
- 模型假设 - 线性模型
- 模型评估 - 损失函数
- 最佳模型 - 梯度下降
- 验证模型好坏
- ERROR
-
- bias大，欠拟合
- var大，过拟合
- K-fold交叉验证
- 梯度下降法（GD）
-
- 调整学习率
-
- 自适应学习率
- Adagrad 算法
- RMSProp 算法
- Adam=RMSProp+Momentum
- Learning Rate Scheduling
- 随机梯度下降（SGD）
- 特征缩放（Feature Normalization）
-
- 标准化
- Batch Normalization
- Internal Covariate Shift
- GD的理论
- 深度学习
-
- 神经网络
-
- 完全连接前馈神经网络
- 模型评估
- 选择最优函数
-
- critical point
- batch和epoch的选取及影响
- GD+Moment
- 反向传播
- Deep Neural Network is better than Fat
- 分类问题
- 卷积神经网络
-
- 经典Receptive field选取方式
- 权值共享
- 池化层
- Flatten
- More Application
机器学习介绍
- 主要包括监督学习、半监督学习、迁移学习、无监督学习、强化学习；
- 监督学习包括回归、分类、结构化学习（没有见过）；
- ML包括DL；
回归
模型步骤
- step1：模型假设，选择模型框架（线性模型）
- step2：模型评估，如何判断众多模型的好坏（损失函数）
- step3：模型优化，如何筛选最优的模型（梯度下降）
模型假设 - 线性模型
一元线性模型（单个特征）
多元线性模型（多个特征）
y = w ∗ x + b y=w*x+b y=w∗x+b
模型评估 - 损失函数
L ( w , b ) = ∑ n = 1 10 ( y ^ n − ( b + w ⋅ x c p ) ) 2 L(w,b)=\sum_{n=1}^{10}\left(\hat{y}^n - (b + w·x_{cp}) \right )^2 L(w,b)=n=1∑10(y^n−(b+w⋅xcp))2
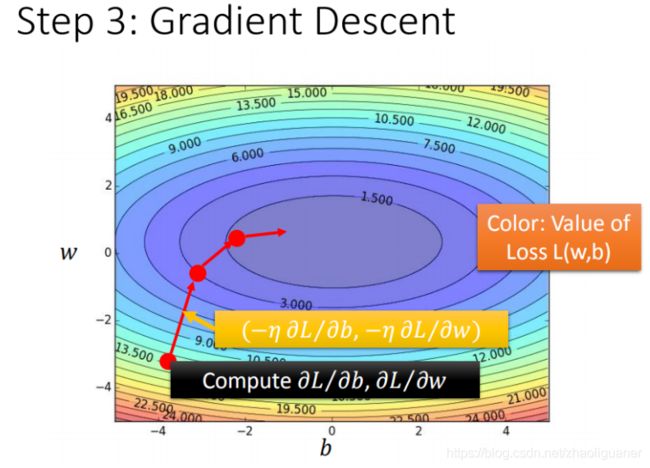
最佳模型 - 梯度下降
- 逐层反向求导
- 在线性回归中，损失函数L是收敛的，即：没有局部最优，线性函数的等高线如下（用于理解）：
- GD的问题
- 问题1：当前最优（Stuck at local minima）
- 问题2：等于0（Stuck at saddle point）
- 问题3：趋近于0（Very slow at the plateau）
验证模型好坏
过拟合问题
解决方法：正则化
欲使损失函数L取值小，则w需要小，从而L的变化小，使得L在变化的过程中较为平滑。
正则化项中，无需加上偏置b，因为b相当于对损失函数图像进行上下平移。
要选择合适的λ，如果过大，使得损失函数L过于平滑，什么都学不到，测试时的误差自然大。
ERROR
error=bias+variance
bias和variance之间的trade-off
bias大，欠拟合
此时应该重新设计模型。因为之前的函数集里面可能根本没有包含 f ∗ f^* f∗。可以：
将更多的函数加进去，比如考虑高度重量，或者HP值等等。
或者考虑更多次幂、更复杂的模型。
如果此时强行再收集更多的data去训练，这是没有什么帮助的，因为设计的函数集本身就不好，再找更多的训练集也不会更好。
var大，过拟合
简单粗暴的方法：
更多的数据；
数据增强(data augmentation)：augment 要augment得有道理；如果你给机器看这种,奇怪的影像的话,它可能就会学到奇怪的东西,所以data augmentation,要根据你对资料的特性,对你现在要处理的问题的理解,来选择合适的,data augmentation的方式；
模型限制：用比较少的features，本来给三天的资料,改成用给两天的资料,其实结果就好了一些。
对模型增加太多限制，会使模型表示力变弱，model bias变大。所以，模型复杂，可能overfitting；增加限制，降低over fitting，但可能Model bias变大，bias和var的trade off问题。
机器学习中的Bias(偏差)，Error(误差)，和Variance(方差)有什么区别和联系？
偏差(Bias)和方差(Variance)——机器学习中的模型选择
K-fold交叉验证
比如，在三份训练结果中，Average错误是模型1最好，再用全部训练集训练模型1。
梯度下降法（GD）
θ ∗ = arg min θ L ( θ ) (1) \theta^∗= \underset{ \theta }{\operatorname{arg\ min}} L(\theta) \tag1 θ∗=θarg minL(θ)(1)
调整学习率
自适应学习率
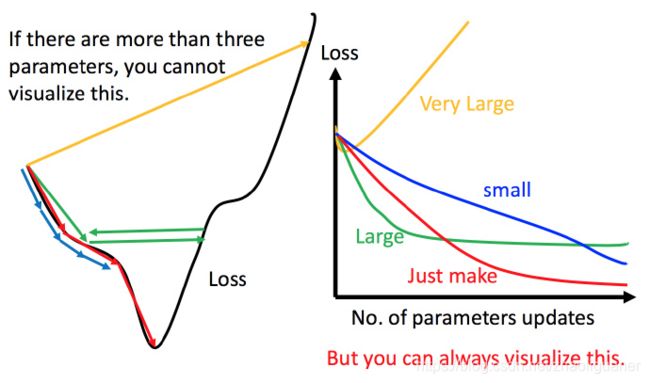
学习率的设置会影响到优化的过程~
- 通常刚开始，初始点会距离最低点比较远，所以使用大一点的学习率
- update好几次参数之后，比较靠近最低点了，此时减少学习率
- 比如 η t = η t t + 1 \eta^t =\frac{\eta^t}{\sqrt{t+1}} ηt=t+1ηt， t t t 是次数。随着次数的增加， η t \eta^t ηt 减小
学习率不能是一个值通用所有特征，不同的参数需要不同的学习率
Adagrad 算法
w t + 1 ← w t − η t σ t g t (5) w^{t+1} \leftarrow w^t -\frac{η^t}{\sigma^t}g^t \tag5 wt+1←wt−σtηtgt(5)
g t = ∂ L ( θ t ) ∂ w (6) g^t =\frac{\partial L(\theta^t)}{\partial w} \tag6 gt=∂w∂L(θt)(6)
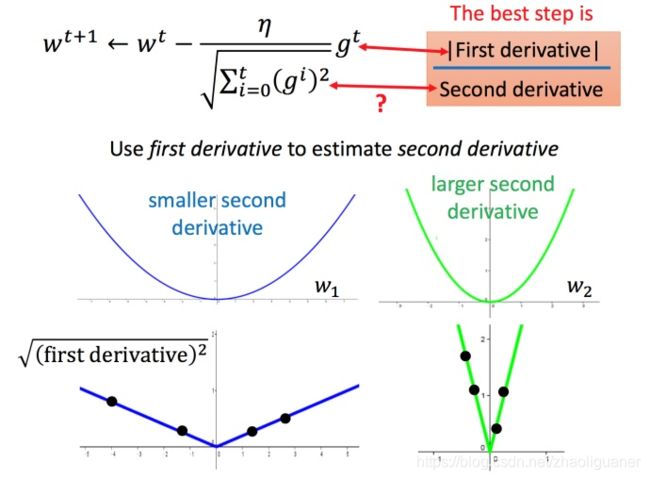
最佳距离 ∣ 2 a x 0 + b 2 a ∣ \left | \frac{2ax_0+b}{2a} \right | ∣∣2a2ax0+b∣∣，还有个分母 2 a 2a 2a 。对function进行二次微分刚好可以得到：
∂ 2 y ∂ x 2 = 2 a (7) \frac{\partial ^2y}{\partial x^2} = 2a \tag7 ∂x2∂2y=2a(7)
所以最好的步伐应该是：
一 次 微 分 二 次 微 分 \frac{一次微分}{二次微分} 二次微分一次微分
即不止和一次微分成正比，还和二次微分成反比。最好的step应该考虑到二次微分：
RMSProp 算法
同一个参数同一个方向，LR也可以动态调整
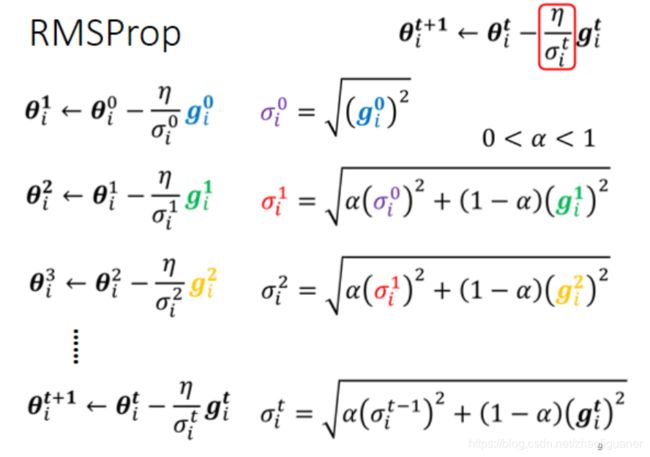
α就像learning rate一样,要自己调它,它是一个hyperparameter
Adam=RMSProp+Momentum
预设参数效果一般更好
Learning Rate Scheduling
- Learning Rate Decay：随著时间的不断进行，随著参数不断的update，让η越来越小
- Warm Up
让learning rate,要先变大后变小；变大要变到多大呢,变大速度要多快呢 ，小速度要多快呢,这个也是hyperparameter,你要自己用手调的,但是大方向的大策略就是,learning rate要先变大后变小。
Residual Network中表明，一开始要设0.01 接下来设0.1,还特别加一个註解说,一开始就用0.1反而就train不好,不知道為什麼
随机梯度下降（SGD）
之前的梯度下降：
L = ∑ n ( y ^ n − ( b + ∑ w i x i n ) ) 2 (8) L=\sum_n(\hat y^n-(b+\sum w_ix_i^n))^2 \tag8 L=n∑(y^n−(b+∑wixin))2(8)
θ i = θ i − 1 − η ▽ L ( θ i − 1 ) (9) \theta^i =\theta^{i-1}- \eta\triangledown L(\theta^{i-1}) \tag9 θi=θi−1−η▽L(θi−1)(9)
而随机梯度下降法更快：
损失函数不需要处理训练集所有的数据，选取一个例子 x n x^n xn
L = ( y ^ n − ( b + ∑ w i x i n ) ) 2 (10) L=(\hat y^n-(b+\sum w_ix_i^n))^2 \tag{10} L=(y^n−(b+∑wixin))2(10)
θ i = θ i − 1 − η ▽ L n ( θ i − 1 ) (11) \theta^i =\theta^{i-1}- \eta\triangledown L^n(\theta^{i-1}) \tag{11} θi=θi−1−η▽Ln(θi−1)(11)
此时不需要像之前那样对所有的数据进行处理，只需要计算某一个例子的损失函数Ln，就可以赶紧update 梯度。GD更稳定，SGD可以更快到达目标。
特征缩放（Feature Normalization）
多组特征的分布范围不一样时，建议将其缩放到同一范围。若不缩放，需要使用不同的学习率来进行参数更新；缩放后，进行参数更新会更有效率。
标准化
做完 normalize 以后啊,这个 dimension 上面的数值就会平均是 0,然后它的 variance就会是 1,所以这一排数值的分布就都会在 0 上下
对每一个 dimension都做一样的 normalization,就会发现所有 feature 不同 dimension 的数值都在 0 上下,那你可能就可以製造一个,比较好的 error surface~
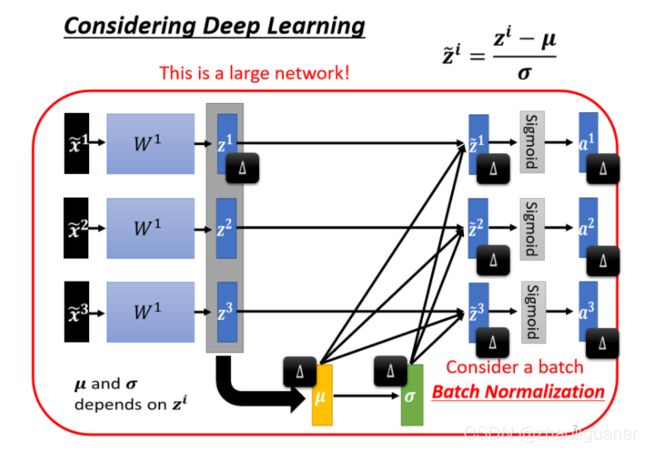
Batch Normalization
只对一个 batch 裡面的 data,做 normalization。Batch Normalization,是适用於 batch size 比较大的时候,因為 batch size 如果比较大,也许这个 batch size 裡面的 data,就足以表示,整个 corpus 的分布,那这个时候你就可以,把这个本来要对整个 corpus,做 Feature Normalization 这件事情,改成只在一个 batch,做 Feature Normalization,作為 approximation。
Internal Covariate Shift
训练集和预测集样本分布不一致的问题就叫做“covariate shift”现象。
Batch Normalization,可以改变 error surface,让 error surface 比较不崎嶇这个观点。
GD的理论
- 参数更新时，未必每次更新都会使损失函数变小
- 利用泰勒展开（泰勒展开可以近似的前提是， x x x无限接近 x 0 x_0 x0）来理解GD，只有当每次移动很小，即学习率很小时，才能成立。所以理论上每次更新参数都想要损失函数减小的话，就需要学习率足够足够小才可以。
- 实际中，当更新参数的时候，如果学习率没有设好，会导致做梯度下降的时候，损失函数没有越来越小。
深度学习
- 神经网络（Neural network）
- 模型评估（Goodness of function）
- 选择最优函数（Pick best function）
神经网络
神经网络也可以有很多不同的连接方式，这样就会产生不同的结构（structure）在这个神经网络里面，我们有很多逻辑回归函数，其中每个逻辑回归都有自己的权重和自己的偏差，这些权重和偏差就是参数。
完全连接前馈神经网络
可以给结构的参数（ w w w， b b b）设置为不同的数，就是不同的函数（function）。这些可能的函数（function）结合起来就是一个函数集（function set）。这个时候函数集（function set）是比较大的，是以前的回归模型（linear model）等没有办法包含的函数（function），所以说深度学习（Deep Learning）能表达出以前所不能表达的情况。
输入和参数之间进行矩阵计算，写成矩阵运算的好处是，可以使用GPU加速，进行并行矩阵运算。
隐藏层：特征转换
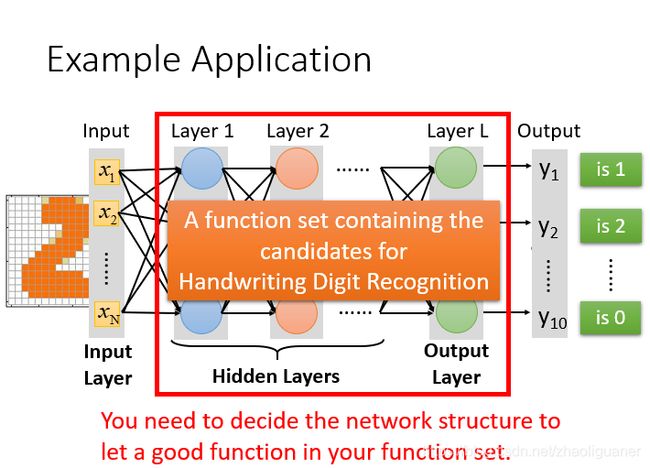
图片表明，神经网络的结构决定了函数集（function set），所以说网络结构（network structured）很关键。
对于有些机器学习相关的问题，我们一般用特征工程来提取特征，但是对于深度学习，我们只需要设计神经网络模型来进行就可以了。对于语音识别和影像识别，深度学习是个好的方法，因为特征工程提取特征并不容易。
模型评估
对于模型的评估，我们一般采用损失函数来反应模型的好差，所以对于神经网络来说，我们采用交叉熵（cross entropy）函数来对 y y y和 y ^ \hat{y} y^的损失进行计算，接下来我们就是调整该模型的参数，让交叉熵越小越好。
对于损失，我们不单单要计算一笔数据的，而是要计算整体所有训练数据的损失，然后把所有的训练数据的损失都加起来，得到一个总体损失L。接下来就是在function set里面找到一组函数能最小化这个总体损失L，或者是找一组神经网络的参数 θ \theta θ，来最小化总体损失L。
选择最优函数
寻找参数：梯度下降
critical point
局部最优和鞍点都有可能导致梯度为0，无法继续下降，判断是局部点还是鞍点~
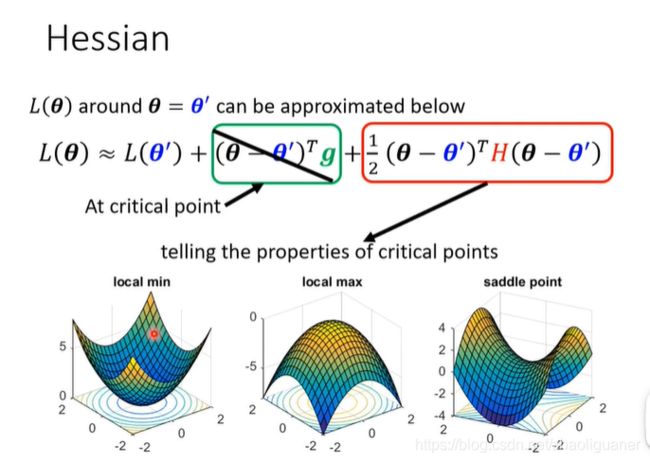
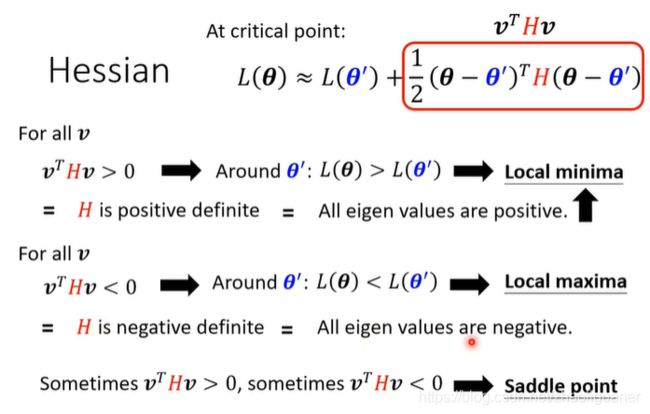
通过Hessen矩阵，可判断是local point还是saddle point；如果是saddle point，向负特征值对应的特征向量的方向走，可使损失函数减小~
常遇到的是saddle point,比较少遇到local minima
batch和epoch的选取及影响
small batch is better on testing data, large batch更容易过拟合。
GD+Moment
training stuck≠small gradient
当Loss不再变化/下降时，梯度还在震荡
反向传播
通过损失进行参数更新，不断优化~
Deep Neural Network is better than Fat
分类问题
pytorch会自动把cross-entropy和softmax集成到一起
batchnormalization可以使得error surface变得平滑，是一个意料之外的发现，还有很多其他归一化方法。
卷积神经网络
讲解从DNN切入，通过对DNN的简化，一步步得到CNN
利用卷积核抓取局部特征~
术语：Convolution Layer, Receptive Field, Filter, Feature Map
经典Receptive field选取方式
- all channels情况下，一般选取kernel_size=3，stride=2或1（希望2个Receptive Field之间有重叠），要去抓取处于图片边边上的pattern，使用padding.
- Network 叠得越深,同样是 3 × 3 的大小的 Filter,它看的范围就会越来越大,所以 Network 够深,你不用怕你侦测不到比较大的 Pattern,它还是可以侦测到比较大的 Pattern~
权值共享
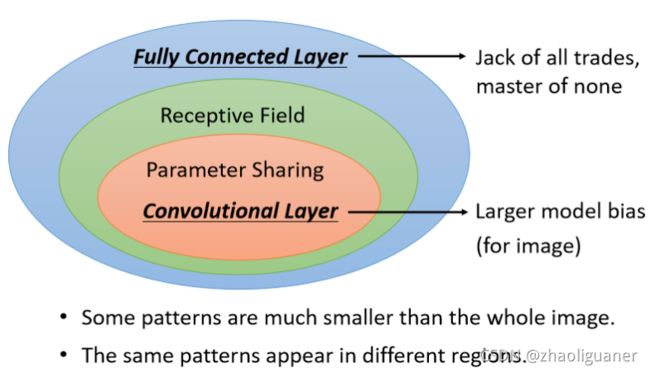对DNN增加了两个限制后得到CNN，CNN的Bias比较大~
Convolutional Layer,它是专门為影像设计的,刚才讲的 Receptive Field 参数共享,这些观察 都是為影像设计的,所以它在影像上仍然可以做得好,虽然它的 Model Bias 很大,但这个在影像上不是问题,但是如果它用在影像之外的任务,你就要仔细想想,那些任务有没有我们刚才讲的,影像用的特性。
池化层
pooling的想法：将图片变小或者去掉某行某列像素，不影响图片的识别~
pooling层没有需要学习的参数，不是一个Layer。最大池化，平均池化~
pooling会将图片的尺寸变小，但是深度不变~
实作中，Convolution 跟 Pooling 交替使用，可能做几次 Convolution,做一次 Pooling,比如两次 Convolution 一次 Pooling。
因為近年来运算能力越来越强,Pooling 最主要的理由是為了减少运算量,做 Subsampling,把影像变少 减少运算量,那如果你今天你的运算资源,足够支撑你不做 Pooling 的话,很多 Network 的架构的设计,往往今天就不做 Pooling,全 Convolution,Convolution 从头到尾,然后看看做不做得起来,看看能不能做得更好
Flatten
将经过conv和pooling的feature map拉平，输入fully connected，经过softmax，得到分类结果。
More Application
想把 CNN 用在语音上和NLP上,你要仔细看一下文献上的方法
在语音上,在文字上,那个 Receptive Field 的设计啊,这个参数共享的设计啊,跟影像上不是一样的，是考虑了语音跟文字的特性以后所设计的
所以不要以為在影像上的 CNN,直接套到语音上它也 Work,可能是不 Work 的,你要想清楚说影像,语音有什麼样的特性,那你要怎麼设计合适的 Receptive Field。
其实 CNN,它没有办法处理影像放大缩小,或者是旋转的问题。
对它来说这两张图片,虽然这个形状是一模一样的,但是如果你把它拉长成向量的话,它裡面的数值就是不一样的啊,所以对 CNN 来说,虽然你人眼一看觉得它形状很像,但对 CNN 的 Network 来说它是非常不一样。
所以事实上,CNN 并不能够处理影像放大缩小,或者是旋转的问题,当它今天在某种大小的影像上,假设你裡面的物件都是比较小的,它在上面学会做影像辨识,你把物件放大它就会整个惨掉
所以 CNN 并没有你想像的那麼强,那就是為什麼在做影像辨识的时候,往往都要做 数据增强，所谓 Data Augmentation 的意思就是说,你把你的训练资料,每张图片都裡面截一小块出来放大,让 CNN 有看过不同大小的 Pattern,然后把图片旋转,让它有看过说,某一个物件旋转以后长什麼样子,CNN 才会做到好的结果。
可以处理scaling和rotation的NN结构——Special Transformer Layer