第6节 蒙特卡罗模拟计算欧式期权价格

第6节 蒙特卡罗模拟计算欧式期权价格

• 6.1 简介
• 6.2 蒙卡模拟计算欧式期权价格算法
• 6.3 算法 Python 代码实现
• 6.4 计算示例
• 6.5 相关说明
  • 6.5.1 股价变化离散化方式
  • 6.5.2 期权价格标准差
  • 6.5.3 离散化点数$N$的选取

6.1 简介

• 蒙特卡罗模拟
         
  蒙特卡罗模拟是一种通过简单的随机抽样来模拟一个随机实验或者随机过程的方法。它主要包括三个部分：
  1. 基本的随机数产生器。一般情况下我们可以直接使用编程语言常用库的随机数产生器。比如Python 中random模块中的random.random()，它可以产生一个在[0, 1]之间的均匀分布的浮点随机数，或者numpy里的random类中包括的均匀分布、正态分布等几种常用随机数产生器。
  2. 需要模拟的随机试验或者随机过程。比如掷骰子，掷飞镖，布朗运动，或者泊松过程。
  3. 如何使用基本的随机数产生器模拟目标实验或者过程。
     
     
     
• 蒙特卡罗模拟股价变化过程
         
  考虑股票价格$S$的变化过程服从几何布朗运动，其连续形式为：
  $$dS=S\mu dt+\sigma dz.$$
  $\mu$为收益率期望值，$\sigma$为股价波动率，$z$为维纳过程，设$\mu$和$\sigma$为常数。股价变化的离散化形式为：
  $$S(t+\Delta t)=S(t)(1+\mu \Delta t+\sigma \epsilon \sqrt{\Delta t}).$$
  其中$\epsilon$为期望值为0，标准差为1的正态分布的一个随机抽样。如果我们将期权有效期0至$T$之间的时间划分为等间隔的$N$段，$\Delta t=T/N$。则我们需要独立地抽取$N$个正态分布随机数，以构成一条股票价格可能的变化路径。
  
  
  
• 蒙特卡罗模拟计算欧式期权价格
         
  为了计算期权价格，我们需要在风险中性世界里模拟股票价格变化过程，即将$\mu$取为无风险利率$r$。按照上述方式我们可以对股票价格变化过程进行抽样。每完成一次对股票价格变化过程的抽样，我们都会得到一个执行时刻$T$时的股票价格，它对应于一个期权价格。我们可以进行$M$次股票变化过程的抽样，将每次最终得到的期权价格放在一起取平均值，即为蒙特卡罗模拟计算出的期权价格。

6.2 蒙卡模拟计算欧式期权价格算法

1. 确定股票价格离散化变化过程，$\Delta t=T/N$, $\epsilon$为一个标准正态分布抽样，则
   $$S(t+\Delta t)=S(t)(1+r\Delta t+\sigma \epsilon \sqrt{\Delta t}).$$
2. 由初始股票价格$S(t=0)=S_0$开始，使用正态分布随机数产生器产生$\epsilon$，根据股票价格离散化变化过程计算得股票价格在$\Delta t$时间后的数值。连续抽样计算直到得到执行时刻的股票价格，完成一次股票价格变化过程的抽样。
3. 由股票价格变化过程的抽样结果计算出相应欧式期权执行时刻的价格。
4. 重复步骤2和3，共$M$次，将$M$个得到的期权价格取算术平均值，然后乘以贴现系数$e^{-rT}$，即得到蒙卡模拟计算欧式期权价格结果。

6.3 算法Python代码实现

import numpy as np
import math 

class Monte_Carlo_European_option:
    def __init__(self, r, sigma, S_0, K, T, N, M):
        self.r = r
        self.sigma = sigma
        self.S_0 = S_0
        self.K = K
        self.T = T
        self.N = N
        self.M = M
        self.call_price = None
        self.put_price = None
    
    def MC_simulation(self):
        self.call_price = 0
        self.put_price = 0
        dt = self.T/self.N
        
        # 抽样 M 次股价变化过程。
        for i in range(self.M):
            S = self.S_0
            # 股价变化过程由 N 次对正态分布抽样构成。
            for j in range(self.N):
                S = S*(1+self.r*dt+self.sigma*dt**0.5*np.random.normal())
                # 另一种离散化表示：
                # S = S*math.e**((self.r-0.5*self.sigma*self.sigma)*dt+self.sigma*dt**0.5*np.random.normal())
            self.call_price += max(0, S-self.K)/self.M
            self.put_price += max(0, self.K-S)/self.M
        
        self.call_price *= math.e**(-self.r*self.T)
        self.put_price *= math.e**(-self.r*self.T)
        
        return

6.4 计算示例

       
考虑当无风险利率为0.05，股价波动率为0.2，初始股价为90，执行价格为100，执行时间为1年后的欧式期权。取$N=400,\Delta t=0.0025$, 进行$M=40000$次蒙卡模拟股价变化过程，并计算期权价格。

MC_obj = Monte_Carlo_European_option(0.05, 0.2, 90, 100, 1, 400, 40000)
MC_obj.MC_simulation()
print("欧式看涨期权价格：{0:.5f}".format(MC_obj.call_price))
print("欧式看跌期权价格：{0:.5f}".format(MC_obj.put_price))
# 解析解：“欧式看涨期权价格为：5.0912， 欧式看跌期权价格为：10.214” 。

欧式看涨期权价格：5.03626
欧式看跌期权价格：10.13694

6.5 相关说明

6.5.1 股价变化过程离散化

       
上面我们使用的股价变化的离散化表示为：
$$S(t+\Delta t)=S(t)(1+r\Delta t+\sigma \epsilon \sqrt{\Delta t}).$$
但如果我们认为股价变化的“真实”过程为连续的几何布朗运动，则由
$$\begin{gathered} d\ln S(t)=(r-\frac{1}{2}{\sigma }^2)dt+\sigma dz, \\ \ln S(t+\Delta t)-\ln S(t)=(r-\frac{1}{2}{\sigma }^2)\Delta t+\sigma \epsilon \sqrt{\Delta t}. \end{gathered}$$
股价变化过程应该为：
$$S(t+\Delta t)=S(t)e^{(r-\frac{1}{2}{\sigma }^2)\Delta t+\sigma \epsilon \sqrt{\Delta t}}.$$
不过我们会看到当$N\to \infty ,\Delta t\to 0$时，按这两种离散化方式计算得出$S(T{)}_1$和$S(T{)}_2$满足同样的分布。
       
记
$$\begin{gathered} S(T{)}_1=S_0\prod _{i=1}^N(1+r\Delta t+\sigma {\epsilon }_i\sqrt{\Delta t}), \\ S(T{)}_2=S_0{e}^{(r-\frac{1}{2}{\sigma }^2)\Delta tN+\sigma \sqrt{\Delta t}{\sum }_{i=1}^N{\epsilon }_i}. \end{gathered}$$
考虑取对数后，
$$\begin{gathered} \ln S(T{)}_1=\ln S_0+\sum _{i=1}^N\ln (1+r\Delta t+\sigma {\epsilon }_i\sqrt{\Delta t}), \\ \ln S(T{)}_2=\ln S_0+(r-\frac{1}{2}{\sigma }^2)\Delta tN+\sigma \sqrt{\Delta t}\sum _{i=1}^N{\epsilon }_i. \end{gathered}$$
将$\ln S(T{)}_1$中对数部分展开，
$$\ln S(T{)}_1=\ln S_0+\sum _{i=1}^N(r\sqrt{\Delta t}+\sigma {\epsilon }_i)\sqrt{\Delta t}-\frac{1}{2}\sum _{i=1}^N(r\sqrt{\Delta t}+\sigma {\epsilon }_i{)}^2\Delta t+\frac{1}{3}\sum _{i=1}^N(r\sqrt{\Delta t}+\sigma {\epsilon }_i{)}^3(\Delta t{)}^{\frac{3}{2}}+...$$
由于$r$和$\sigma$不变，忽略$\Delta t^{\frac{3}{2}}$项（当$N\to \infty$时为0）后，
$$\ln S(T{)}_1=\ln S_0+r\Delta tN+\sigma \sqrt{\Delta t}\sum _{i=1}^N{\epsilon }_i-\frac{1}{2}{\sigma }^2\Delta t\sum _{i=1}^N{\epsilon }_i^2.$$
当$N\to \infty ,N\Delta t=T$，$\frac{1}{N}{\sum }_{i=1}^N{\epsilon }_i^2=1,{\sum }_{i=1}^N{\epsilon }_i\sim \sqrt{N}\epsilon$，所以
$$\begin{gathered} \ln S(T{)}_1\sim \ln S_0+(r-\frac{1}{2}{\sigma }^2)T+\sigma \sqrt{T}\epsilon , \\ \ln S(T{)}_1\sim \mathcal{N}(\ln S_0+(r-\frac{1}{2}{\sigma }^2)T,\sigma \sqrt{T}). \end{gathered}$$
而且易见$\ln S(T{)}_2\sim \mathcal{N}(\ln S_0+(r-\frac{1}{2}{\sigma }^2)T,\sigma \sqrt{T})$。
       
所以当$N$趋于无穷大时，两种离散化方式抽样所得的$S(T)$的分布是相同的，而且就为股价服从连续的几何布朗运动时的$S(T)$分布。

6.5.2 期权价格标准差

       
蒙卡模拟计算的期权价格为$M$次股价变化过程抽样结果对应期权价格的平均值并贴现。如果每一次股价抽样所得的期权价格的标准差为$\omega$，则$M$次蒙卡模拟计算的期权价格的标准差为:
$$\frac{\omega }{\sqrt{M}}.$$
以欧式看涨期权为例，
$${\omega }^2={\int }_0^{+\infty }f(S_T)e^{-2rT}[\max (S_T-K,0){]}^{2}d{S}_T-c^2.$$
其中$f(S_T)$为执行时刻股价分布的概率密度函数，$K$为期权执行价格，$c$为欧式看涨期权的价格。下面略去计算过程，我们有
$$\begin{gathered} c=S_{0}N(d_1)-K{e}^{-rT}N(d_2),d_1=\frac{\ln \frac{S_0}{K}+(r+\frac{1}{2}{\sigma }^2)T}{\sigma \sqrt{T}},d_2=d_1-\sigma \sqrt{T}, \\ f(S_T)=\frac{1}{S_T}\frac{1}{\sqrt{2\pi }{\sigma }_0}{e}^{-\frac{(\ln S_T-{\mu }_0{)}^2}{2{\sigma }_0^2}},{\sigma }_0=\sigma \sqrt{T},{\mu }_0=\ln S_0+(r-\frac{1}{2}{\sigma }^2)T. \end{gathered}$$
代入${\omega }^2$的表达式，计算得：
$${\omega }^2=K^2{e}^{-2rT}N(d_2)-2K{S}_0{e}^{-rT}N(d_1)+S_0^2{e}^{{\sigma }^{2}T}N(\frac{\ln \frac{S_0}{K}+(r+\frac{3}{2}{\sigma }^2)T}{\sigma \sqrt{T}})-[S_{0}N(d_1)-K{e}^{-rT}N(d_2){]}^2.$$
考虑上面计算示例中，无风险利率为0.05，股价波动率为0.2，初始股价为90，执行价格为100，执行时间为1年后的欧式看涨期权。代入相关参数，得
$$\omega =10.162.$$
我们抽样股价路径$M=40000$次后，计算出的欧式看涨期权价格的标准差为
$$\frac{\omega }{\sqrt{M}}=\frac{10.162}{200}=0.05081.$$

6.5.3 离散化点数$N$的选取

       
进行蒙特卡罗模拟抽样计算期权价格时，误差的来源有两方面。一方面是上面我们计算的和股价变化路径抽样数量$M$相关的误差，另一方面是我们在对股票价格变化过程离散化时产生的误差（相对于连续变化时股价最终分布的差别）。由6.5.1中讨论知当离散化点数$N$趋于无穷大时，我们对股价变化过程的抽样模拟将和股价按连续几何布朗运动的结果相同。
       
下面我们定量地测试选取不同$N$时，期权价格计算结果会如何变化。这里我们使用和示例中一样的参数，但是取$M$为36万，这样会使得$\omega /\sqrt{M}\approx 0.02$，即使与抽样股价路径数量相关的误差很小。得下图，

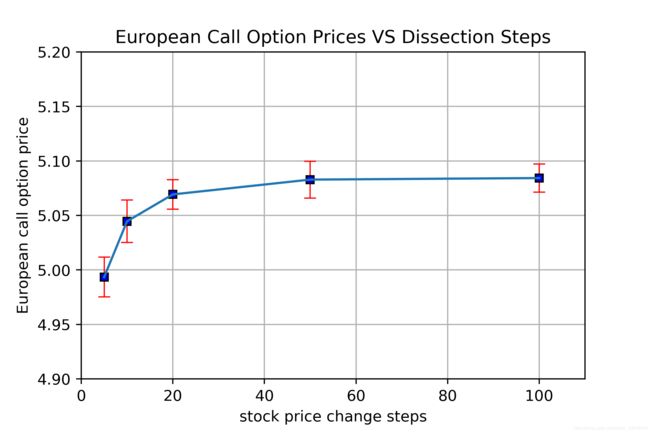
其中每个数值点为按上述蒙卡抽样计算期权价格25次后的平均值，数值点上的置信区间为$[-\sigma ,\sigma ]$。由于我们可以使用欧式看涨期权解析解计算得期权价格应该为5.0912，通过上图可见，当我们选取$N>50$之后，蒙卡模拟计算所得期权价格已经比较接近解析解结果了。

# Appendix.

# Calculate call prices vs Ns.
k = 25
Ns = []
prices = []

for N in [5, 10, 20, 50, 100]:
    for _ in range(k):
        Ns.append(N)
        MC_obj = Monte_Carlo_European_option(0.05, 0.2, 90, 100, 1, N, 360000)
        MC_obj.MC_simulation()
        prices.append(MC_obj.call_price)

# Make plot.
import matplotlib.pyplot as plt
import matplotlib.lines as lines
import numpy as np

fig = plt.figure()
ax1 = fig.add_subplot(1, 1, 1)

k = 25
X = [5, 10, 20, 50, 100]
Y = []
errors = []
for i in range(5):
    Y.append(np.average(prices[k*i:k*(i+1)]))
    errors.append(np.std(prices[k*i:k*(i+1)]))

ax1.plot(X, Y, color="yellow", marker="s", linewidth=0.9, ms=5, mfc="blue", mec="black")
ax1.errorbar(X, Y, errors, ecolor="red", capsize=4, capthick=0.8, elinewidth=0.8)

# line1 = lines.Line2D([5, 100], [5.0912, 5.0912], lw=1, color="black", transform=ax1.transAxes)
# ax1.lines.append(line1)

ax1.axis((0, 110, 4.9, 5.15))
ax1.set_xlabel("stock price change steps")
ax1.set_ylabel("European call option price")
ax1.set_title("European Call Option Prices VS Dissection Steps")
ax1.grid(True)

fig.savefig("6_1.png", dpi=400)
fig.show()

参考资料：

1. 《期权、期货及其他衍生产品》，John C. Hull 著，王勇、索吾林译 。