java位的概念_【JAVA基础】二进制基本概念及位运算
0 前言
二进制的相关概念是学习数据存储、数据压缩、数据序列化的基石,只有真正搞清楚了二进制,才能逐步深入到算法源码,达到理解和复现的目的。
本文将介绍二进制和数据存储的相关概念(包括位、字节、高低位、大小端、原码、反码、补码、进制转换),以及二进制的位运算。
注意:本文讲解偏实战,有些定义不够严谨,如需深入研究可以进一步阅读
https://zhuanlan.zhihu.com/p/...
1 基本概念
1.1 位、字节
位(bit):计算机内部存储数据的最小单位。
字节(Byte):计算机存储容量(数据处理)的基本单位,1byte (字节)= 8 bit(位)。无符整型取值范围0~255,有符整型取值范围-128~127。
1byte = 8bit = 8二进制位 = 2个十六进制位
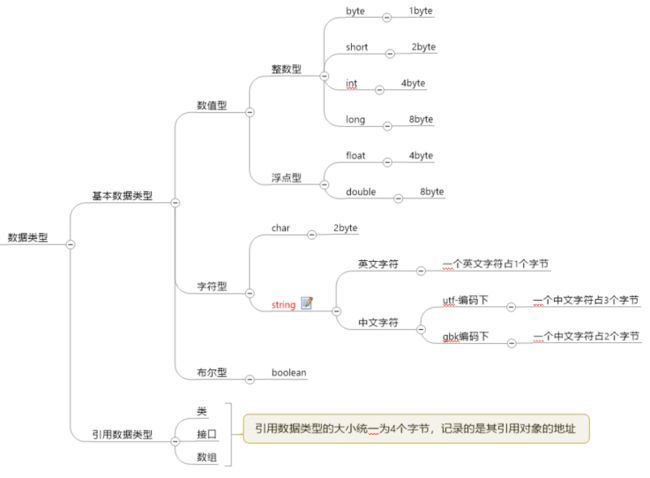
JAVA中数据类型的占用内存大小如图所示:
注意,string其实不属于基本数据类型,为便于对比将其放入字符型。
1.2 高位、低位、符号位
高位:指在数据类型限定范围内靠左的二进制位。
低位:指在数据类型限定范围内靠右的二进制位。
符号位:指在数据类型限定范围内最左边的一个二进制位,符号位为0表示正数,1表示负数。
【举例说明】
十进制数1的二进制为:0000 0001(最左边的0为符号位,从左往右对应的是高位向低位延伸)
十进制数-1的二进制为:1111 1111(最左边的1为符号位,从左往右对应的是高位向低位延伸)
【扩展】为什么-1的二进制位不是1000 0001呢?
1.3 大小端
对于一个字节序列,如何解析?究竟是从左读还是从右读?正因为有了读写顺序的差异,带来了两种不同的模式。
【定义】
大端模式(Big-endian),是指数据的高字节位 保存在 内存的低地址中,而数据的低字节位 保存在 内存的高地址中。这样的存储模式有点儿类似于把数据当作字符串顺序处理:地址由小向大增加,而数据从高位往低位放。和我们”从左到右“阅读习惯一致。简言之,高位字节在前,低位字节在后。
小端模式(Little-endian),是指数据的高字节位 保存在 内存的高地址中,而数据的低字节位 保存在 内存的低地址中。这种存储模式将地址的高低位和数据位有效地结合起来,高地址部分权值高,低地址部分权值低,和我们的逻辑方法一致。简言之,低位字节在前,高位字节在后。
比如字节数据0x1A2B3C4D
内存的低位地址----------->内存的高位地址
大端模式:1A 2B 3C 4D
小端模式:4D 3C 2B 1A
【特点】
大端:符号位在所表示的数据内存的第一个字节中,便于快速判断数据的正负和大小(CPU做数值运算时从内存中依顺序依次从低位地址到高位地址取数据进行运算,大端就会最先拿到数据的(高字节的)符号位)。
小端:CPU做数值运算时从内存中依顺序依次从低位地址到高位地址取数据进行运算,开始只管取值,最后刷新最高位地址的符号位就行,这样的运算方式会更高效一些。
目前我们常见的CPU PowerPC、IBM是大端模式,x86是小端模式。ARM既可以工作在大端模式,也可以工作在小端模式,一般ARM都默认是小端模式。一般通讯协议都采用的是大端模式。
1.4 原码、反码、补码
暂不深究定义,从应用的角度,可以将原码、反码和补码联系在一起理解,就是计算相反数,即
原码的相反数=原码的补码=原码的反码(在原码基础上按位取反)+1
【举例说明】
原码=0000 0001(十进制为1)
反码=原码按位取反=1111 1110
补码=反码+1=1111 1111(十进制为-1)=-原码
若原码为-1,同样的运算可以得到其补码为1,因此,对于计算相反数而言,原码和补码是个相对概念。
通过java程序验证:
import org.junit.Test;
public class binaryTest {
public void print(int value){
System.out.println("value="+value+",其二进制串为(左侧的0省略):"+Integer.toBinaryString(value));
}
@Test
public void test(){
int i=-1;
print(i); // 原码
print(~i); // 反码
print(~i+1); // 补码
}
【扩展】
如何用二进制表示浮点数?为何会有精度损失?
1.5 进制的表示与转换
JAVA中的进制表示及转换:
@Test
public void convert(){
// 二进制表示--用0b
System.out.println(0b101);
// 十六进制表示--用0x
System.out.println(0x101);
// 二进制转十进制
System.out.println(Integer.valueOf("101",2));
// 十六进制转十进制
System.out.println(Integer.valueOf("a",16));
// 十进制转二进制
System.out.println(Integer.toBinaryString(10));
// 十进制转十六进制
System.out.println(Integer.toHexString(10));
}
运行结果如下:
5
257
5
10
1010
a
2 位运算
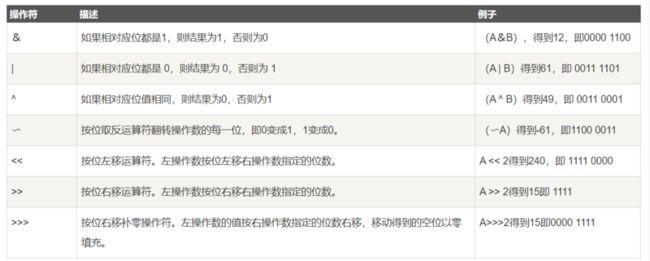
2.1 与、或、非、异或
假设A = 60,B = 13;它们的二进制格式表示将如下:
A = 0011 1100
B = 0000 1101
-----------------
A&B = 0000 1100
A|B = 0011 1101
A^B = 0011 0001
~A = 1100 0011
2.2 有符号左移<<
定义:a
注意:当n=size-1时(size指位数,如1btye的size=8),符号位改变,数值发生极端变化。
JAVA代码验证如下:
@Test
public void zuoyi(){
int i=1;
System.out.println("================原始数据===============");
print(i);
System.out.println("================左移1位===============");
print(i<<1);
System.out.println("================左移31位===============");
print(i<<31);
int j =-1;
System.out.println("================原始数据===============");
print(j);
System.out.println("================左移1位===============");
print(j<<1);
System.out.println("================左移31位===============");
print(j<<31);
}
运行结果如下:
================原始数据===============
value=1,其二进制串为(左侧的0省略):1
================左移1位===============
value=2,其二进制串为(左侧的0省略):10
================左移31位===============
value=-2147483648,其二进制串为(左侧的0省略):10000000000000000000000000000000
================原始数据===============
value=-1,其二进制串为(左侧的0省略):11111111111111111111111111111111
================左移1位===============
value=-2,其二进制串为(左侧的0省略):11111111111111111111111111111110
================左移31位===============
value=-2147483648,其二进制串为(左侧的0省略):10000000000000000000000000000000
2.3 有符号右移>>
定义:a>>n,即a整体右移n位,低位丢弃,正数高位补零,负数高位补一。
特点:每右移一位,相当于该数除以2(向下取整)。
注意:当n大于原实际有效位数时,正数的最终结果为0,负数的最终结果为-1。
JAVA代码验证如下:
@Test
public void youyi(){
int i=5;
System.out.println("================原始数据===============");
print(i);
System.out.println("================右移1位===============");
print(i>>1);
System.out.println("================右移2位===============");
print(i>>2);
System.out.println("================右移3位===============");
print(i>>3);
int j =-5;
System.out.println("================原始数据===============");
print(j);
System.out.println("================右移1位===============");
print(j>>1);
System.out.println("================右移2位===============");
print(j>>2);
System.out.println("================右移3位===============");
print(j>>3);
}
运行结果如下:
================原始数据===============
value=5,其二进制串为(左侧的0省略):101
================右移1位===============
value=2,其二进制串为(左侧的0省略):10
================右移2位===============
value=1,其二进制串为(左侧的0省略):1
================右移3位===============
value=0,其二进制串为(左侧的0省略):0
================原始数据===============
value=-5,其二进制串为(左侧的0省略):11111111111111111111111111111011
================右移1位===============
value=-3,其二进制串为(左侧的0省略):11111111111111111111111111111101
================右移2位===============
value=-2,其二进制串为(左侧的0省略):11111111111111111111111111111110
================右移3位===============
value=-1,其二进制串为(左侧的0省略):11111111111111111111111111111111
2.4 无符号右移>>>
定义:a>>>n,即a整体右移n位,低位丢弃,高位正数补零。
特点:若a为正数,则>>>与>>效果一样;若a为负数,移动后均转为正数。
@Test
public void youyi2(){
int i=5;
System.out.println("================原始数据===============");
print(i);
System.out.println("================右移1位===============");
print(i>>>1);
System.out.println("================右移2位===============");
print(i>>>2);
System.out.println("================右移3位===============");
print(i>>>3);
int j =-5;
System.out.println("================原始数据===============");
print(j);
System.out.println("================右移1位===============");
print(j>>>1);
System.out.println("================右移2位===============");
print(j>>>2);
System.out.println("================右移3位===============");
print(j>>>3);
}
运行结果如下:
================原始数据===============
value=5,其二进制串为(左侧的0省略):101
================右移1位===============
value=2,其二进制串为(左侧的0省略):10
================右移2位===============
value=1,其二进制串为(左侧的0省略):1
================右移3位===============
value=0,其二进制串为(左侧的0省略):0
================原始数据===============
value=-5,其二进制串为(左侧的0省略):11111111111111111111111111111011
================右移1位===============
value=2147483645,其二进制串为(左侧的0省略):1111111111111111111111111111101
================右移2位===============
value=1073741822,其二进制串为(左侧的0省略):111111111111111111111111111110
================右移3位===============
value=536870911,其二进制串为(左侧的0省略):11111111111111111111111111111
参考目录