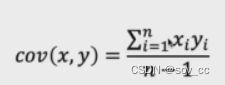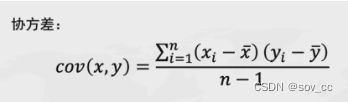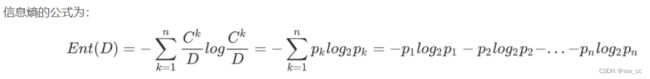用python对数据进行主成分分析、类概念描述及特征化分析-实验报告

数据挖掘课程的期中实验，仅供参考。完成时间：2022.10.29
基本要求：利用python对数据集中的数据进行主成分分析、类概念描述及特征化分析。要有相关结果的可视化结果。比如数据的分布情况。
数据源是TCGA。
数据源、代码相关文章：https://blog.csdn.net/Coral__/article/details/128483047

一、主成分分析（PCA）

1.理论学习

无监督学习就是没有y，让算法从特征变量x里面自己寻找特征。

主成分分析，可以将数据进行线性变化从而进行降维，用少数几个变量代替原始的很多的变量。但是主成分不能进行变量筛选，因为新的变量是原始变量的线性组合，失去了原有的含义。而和主成分很像的因子分析可以进行部分解释。

算法的具体步骤如下：
1）对向量X进行去中心化。（把坐标原点放到数据中心）
2）计算向量X的协方差矩阵，自由度可以选择0或者1。
3）计算协方差矩阵的特征值和特征向量。
4）选取最大的k个特征值及其特征向量。
5）用X与特征向量相乘。

数据的线性变化：

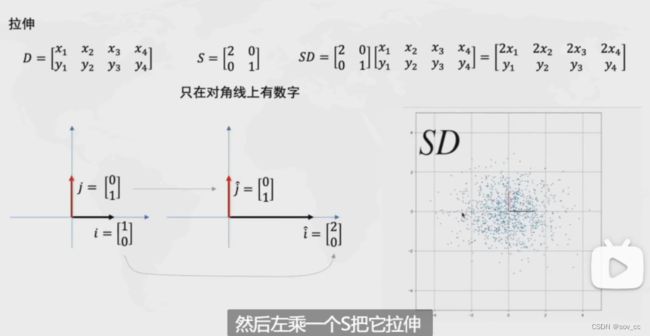
拉伸

（x轴拉伸了两倍，y轴不变）

旋转

（逆时针旋转了θ度）

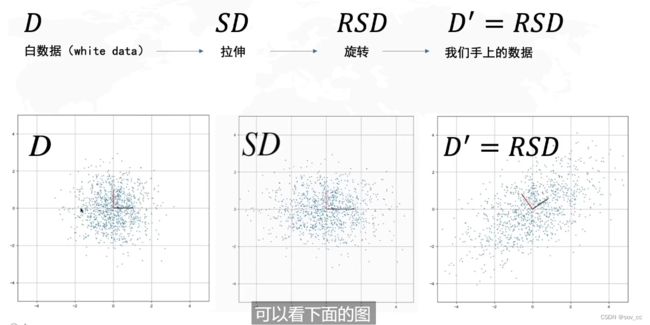
总流程

我们需要求出R，求出R的时候就找到了PCA想要的坐标系

协方差矩阵的特征向量就是R

对于本题来说（平均值为原点），协方差计算：

原本：

最终公式推导：

R就是后面新坐标轴的两个特征向量相乘

2.实验目的

在本次实验中，我们使用的数据库是TCGA，是美国国家癌症研究所和美国人类基因研究所共同监督的一个项目，旨在应用高通量的基因组分析技术，以帮助人们对癌症有更好的认知，从而提高对于癌症的预防、诊断和治疗能力。

在实验过程中，我以BLCA（肾上腺皮质癌）的数据为例子，一步一步表明如何进行主成分分析。

3.实验过程（以BLCA为例）

0）导入包和数据：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.model_selection import cross_val_score#交叉val值
from sklearn.linear_model import LinearRegression#线性回归
from sklearn.model_selection import LeaveOneOut
from mpl_toolkits import mplot3d
 
data = pd.read_csv('C:\\Users\\coral\\Desktop\\BLCA\\rna.csv')
data = data.iloc[:,1:]#去掉第一列无用的索引
len = data.shape[1]#返回列数,后续经常会用到

无监督学习就是没有y，所以我们需要去掉第一列的索引。

1）数据标准化：

#实例化
scaler = StandardScaler()
# 训练
scaler.fit(data)  
# 返回转换后的数据
X = scaler.transform(data)  

2）主成分pca拟合：

#主成分PCA拟合
model = PCA()
model.fit(X)  # 用数据集X拟合模型
#每个主成分能解释的方差。代表降维后的各主成分的方差值。方差值越大，则说明越是重要的主成分
model.explained_variance_
#每个主成分能解释的方差的百分比。代表降维后的各主成分的方差值占总方差值的比例，这个比例越大，则越是重要的主成分
model.explained_variance_ratio_

#可视化
plt.plot(model.explained_variance_ratio_, marker='o', markersize=2)

plt.xlabel('主成分分析')
plt.ylabel('方差解释比例')
plt.title('PCA')

plt.show()

3）计算累计百分比，这样可以判断选几个主成分：

# 画累计百分比，这样可以判断选几个主成分
x=range(1.len+1)
y=model.explained_variance_ratio_.cumsum()

plt.plot(x,y, marker='o', markersize=2)
plt.xlabel('主成分分析')
plt.ylabel('方差解释比例的百分比')
plt.axhline(0.9, color='k', linestyle='--', linewidth=1)

print(y)

#标出前三个主成分的占比
r=0
for a, b in zip(x, y):
    r+=1
    plt.text(a, b, b)
    if r>=3:
        break

plt.title('Cumulative PVE/累计百分数')

plt.show()

由图可知接近60个主成分能解释到90%以上了。

print的结果：

我们可以得到第一主成分占比68.797768%，第二主成分占比4.724263%，第三主成分占比2.709897%

4）主成分载荷矩阵

model.components_

columns = ['TCGA' + str(i) for i in range(1, len+1)]

pca_loadings = pd.DataFrame(model.components_, columns=data.columns, index=columns)
round(pca_loadings, 2)

该矩阵用于展示每个主成分原始数据的线性组合，以及线性的系数。

5）计算每个样本的主成分得分

# PCA Scores
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用于正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False#用于正常显示负数

pca_scores = model.transform(X)
pca_scores = pd.DataFrame(pca_scores, columns=columns)
pca_scores.shape
pca_scores.head()

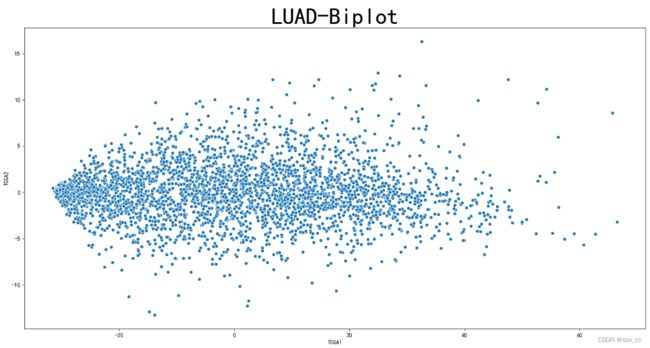
6）前两个主成分的可视化，散点图

sns.scatterplot(x='TCGA1', y='TCGA2', data=pca_scores)
plt.title('Biplot',fontsize=40)

plt.show()

7）三个主成分的可视化图，三维图

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(pca_scores['TCGA1'], pca_scores['TCGA2'], pca_scores['TCGA3'], c='b')
ax.set_xlabel('TCGA1')
ax.set_ylabel('TCGA2')
ax.set_zlabel('TCGA3')

plt.show()

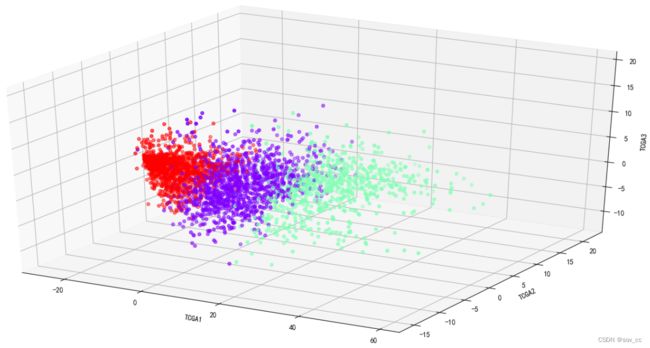
8）利用K均值聚类对三个主成分聚类，可视化

model = KMeans(n_clusters=3, random_state=1, n_init=20)
model.fit(X)
model.labels_

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(pca_scores['TCGA1'], pca_scores['TCGA2'], pca_scores['TCGA3'],
           c=model.labels_, cmap='rainbow')
ax.set_xlabel('TCGA1')
ax.set_ylabel('TCGA2')
ax.set_zlabel('TCGA3')

plt.show()

9）总代码-生成散点图版

from sklearn.cluster import KMeans
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.model_selection import cross_val_score#交叉val值
from sklearn.linear_model import LinearRegression#线性回归
from sklearn.model_selection import LeaveOneOut
from mpl_toolkits import mplot3d
 
data = pd.read_csv('C:\\Users\\coral\\Desktop\\shujuwajue\\data\\BLCA\\rna.csv')
data = data.iloc[:,1:]#去掉第一列无用的索引
len = data.shape[1]#返回列数,后续经常会用到
#数据标准化	
#实例化
scaler = StandardScaler()
# 训练
scaler.fit(data)  
# 返回转换后的数据
X = scaler.transform(data)  

#主成分PCA拟合
model = PCA()
model.fit(X)  # 用数据集X拟合模型
#每个主成分能解释的方差。代表降维后的各主成分的方差值。方差值越大，则说明越是重要的主成分
model.explained_variance_
#每个主成分能解释的方差的百分比。代表降维后的各主成分的方差值占总方差值的比例，这个比例越大，则越是重要的主成分
model.explained_variance_ratio_

# #可视化
# plt.plot(model.explained_variance_ratio_, marker='o', markersize=2)

# plt.xlabel('主成分分析')
# plt.ylabel('方差解释比例')
# plt.title('PCA')

# plt.show()

# # 画累计百分比，这样可以判断选几个主成分
# x=range(1,len+1)
# y = model.explained_variance_ratio_.cumsum()

# plt.plot(x,y, marker='o', markersize=3)
# plt.xlabel('主成分分析')
# plt.ylabel('方差解释比例的百分比')
# plt.axhline(0.9, color='k', linestyle='--', linewidth=1)

# # print(y)

# #标出前三个主成分的占比
# r=0
# for a, b in zip(x, y):
#     r+=1
#     plt.text(a, b, b)
#     if r>=3:
#         break

# plt.title('BLCA-Cumulative PVE/累计百分数',fontsize=20)

# plt.show()

#主成分核载矩阵
model.components_

columns = ['TCGA' + str(i) for i in range(1, len+1)]

pca_loadings = pd.DataFrame(model.components_, columns=data.columns, index=columns)
round(pca_loadings, 2)

# PCA Scores
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用于正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False#用于正常显示负数

pca_scores = model.transform(X)
pca_scores = pd.DataFrame(pca_scores, columns=columns)
pca_scores.shape
pca_scores.head()

#前两个主成分的可视化

sns.scatterplot(x='TCGA1', y='TCGA2', data=pca_scores)
plt.title('Biplot',fontsize=40)

plt.show()

# #三个主成分的可视化图，三维图
# fig = plt.figure()
# ax = fig.add_subplot(111, projection='3d')
# ax.scatter(pca_scores['TCGA1'], pca_scores['TCGA2'], pca_scores['TCGA3'], c='b')
# ax.set_xlabel('TCGA1')
# ax.set_ylabel('TCGA2')
# ax.set_zlabel('TCGA3')

# plt.show()

# #利用K均值聚类对三个主成分聚类，可视化
# model = KMeans(n_clusters=3, random_state=1, n_init=20)
# model.fit(X)
# model.labels_

# fig = plt.figure()
# ax = fig.add_subplot(111, projection='3d')
# ax.scatter(pca_scores['TCGA1'], pca_scores['TCGA2'], pca_scores['TCGA3'],
#            c=model.labels_, cmap='rainbow')
# ax.set_xlabel('TCGA1')
# ax.set_ylabel('TCGA2')
# ax.set_zlabel('TCGA3')

# plt.show()

4.不同种类癌症对比

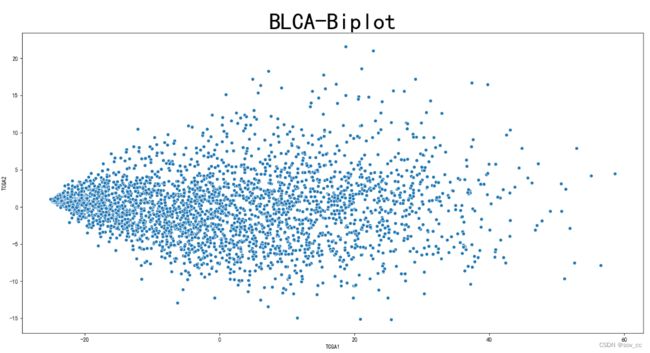
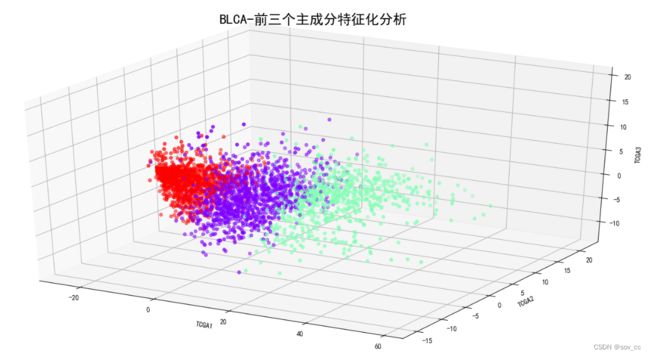
1.BLCA

第一主成分占比68.80%，第二主成分占比4.72%，第三主成分占比2.71%。

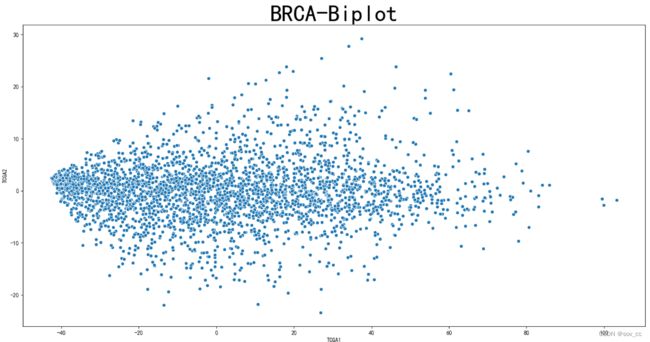
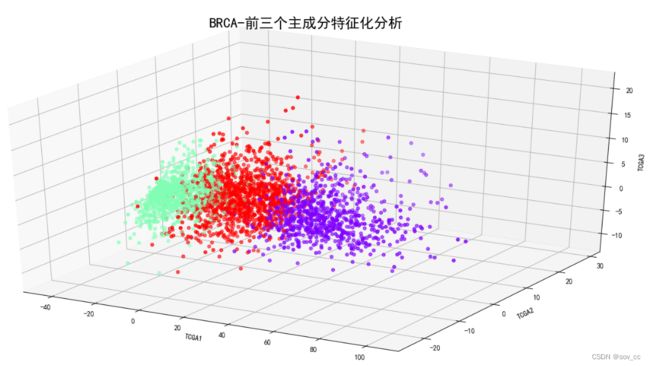
2.BRCA

第一主成分占比76.55%，第二主成分占比1.35%，第三主成分占比0.94%。

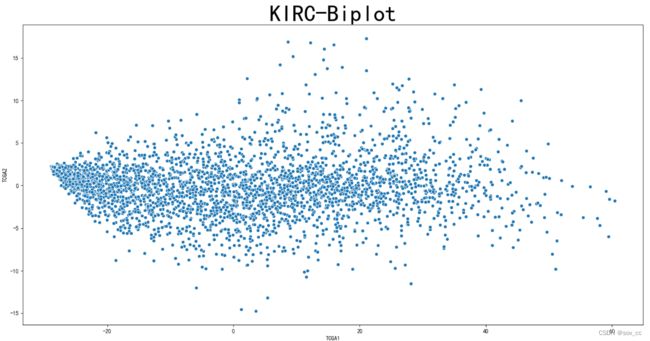
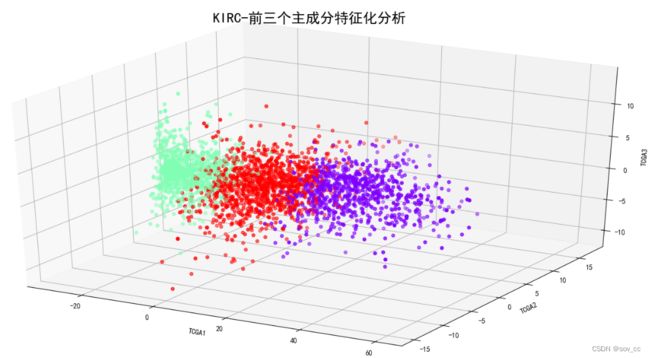
3.KIRC

第一主成分占比80.69%，第二主成分占比1.52%，第三主成分占比1.02%。

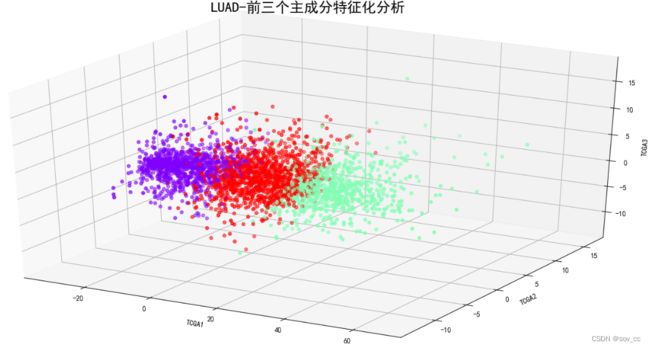
4.LUAD

第一主成分占比75.75%，第二主成分占比1.60%，第三主成分占比1.22%。

5.PAAD

第一主成分占比78.38%，第二主成分占比2.48%，第三主成分占比1.69%。

二、类概念描述及特征化分析

概念描述是指为数据的特征化和比较产生描述。

数据概化就是将数据库中的跟任务相关的数据集从较低的概念层抽象到较高的概念层的过程。

1.类特征化和类对比分析

• 数据特征化是目标数据的一般特性或特性的汇总。

• 数据对比分析是将目标类数据对象的一个特性与一个或多个对比类对象的一般特性进行比较。

特征类型判断以及处理是前期特征工程重要的一环，也是决定特征质量好坏和权衡信息丢失最重要的一环。

按照数据存储的数据格式可以归纳为两类：

按照特征数据含义又可分为：

离散型随机变量：取值只能是可取范围内的指定数值类型的随机变量，比如年龄、车流量此类数据。
连续随机变量：按照测量或者计算方法得到，在某个范围内连取n个值，此类数据可化为定类数据。
二分类数据：此类数据仅只有两类：例如是与否、成功与失败。
多分类数据：此类数据有多类：例如天气出太阳、下雨、阴天。
周期型数据：此类数据存在一个周期循环：例如周数月数。

2.类特征化分析-实操

在实际工作场景中，样本数据往往会包含多个特征，而且通过业务经验是无法区分类别的，因此必然需要借助于相关聚类算法进行实现。常用的聚类算法包括K-means、DBSCAN等，都可以有效划分样本的类别属性。我们先进行PCA，然后采用K-means聚类算法。

如下图，是癌症数据集前三个主成分的可视化图表：

代码：

from sklearn.cluster import KMeans
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.model_selection import cross_val_score  # 交叉val值
from sklearn.linear_model import LinearRegression  # 线性回归
from sklearn.model_selection import LeaveOneOut
from mpl_toolkits import mplot3d

data = pd.read_csv(
    'C:\\Users\\coral\\Desktop\\shujuwajue\\data\\PAAD\\rna.csv')
data = data.iloc[:, 1:]  # 去掉第一列无用的索引
len = data.shape[1]  # 返回列数,后续经常会用到

#采用z-score标准化（归一化）数据标准化
#实例化
scaler = StandardScaler()
# 训练
scaler.fit(data)
# 返回转换后的数据
X = scaler.transform(data)
#主成分PCA拟合
model = PCA()
model.fit(X)  # 用数据集X拟合模型
#每个主成分能解释的方差。代表降维后的各主成分的方差值。方差值越大，则说明越是重要的主成分
model.explained_variance_
#每个主成分能解释的方差的百分比。代表降维后的各主成分的方差值占总方差值的比例，这个比例越大，则越是重要的主成分
model.explained_variance_ratio_

#主成分核载矩阵
model.components_

columns = ['TCGA' + str(i) for i in range(1, len+1)]

pca_loadings = pd.DataFrame(
    model.components_, columns=data.columns, index=columns)
round(pca_loadings, 2)  # 四舍五入到指定的2位小数

# PCA Scores

pca_scores = model.transform(X)
pca_scores = pd.DataFrame(pca_scores, columns=columns)
pca_scores.shape
# 读取矩阵的长度，比如shape[0]就是读取矩阵第一维度的长度。
pca_scores.head()
#head()函数是查看向量，矩阵或数据框等数据的部分信息，它默认输出数据框前6行数据，与其相对的是tail()，查看的是数据框最后的6行数据。
# 两者都可以添加一个参数n来控制显示的行数。

plt.rcParams['font.sans-serif'] = ['SimHei']  # 用于正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用于正常显示负数

#利用K均值聚类对三个主成分聚类，可视化
model = KMeans(n_clusters=3, random_state=1, n_init=20)
model.fit(X)
model.labels_

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(pca_scores['TCGA1'], pca_scores['TCGA2'], pca_scores['TCGA3'],
           c=model.labels_, cmap='rainbow')
ax.set_xlabel('TCGA1')
ax.set_ylabel('TCGA2')
ax.set_zlabel('TCGA3')

plt.title("PAAD-前三个主成分特征化分析", fontsize=20)

plt.show()

3.类对比分析-实操

结果分析：

通过图像分析可得：每种癌症类型选了10个样本，前15个基因，可视化后发现这10个患者对应基因的表达情况很接近。

代码：

import matplotlib.pyplot as plt
import matplotlib.transforms as mtrans
import pandas as pd
import numpy as np
import os
from pathlib import Path

l1 = []  # 用来存储CPU总利用率
l2 = []
l3 = []
l4 = []
l5 = []
l6 = []
l7 = []
l8 = []
l9 = []
l10 = []
x=[]

file = pd.read_csv(
    "C:\\Users\\coral\\Desktop\\shujuwajue\\data\\PAAD\\rna.csv")
file = file.iloc[1:, :]  # 去掉第一行无用的索引
len = file.shape[0]  # 返回行数

f = np.array(file)

i=0
for item in f:
    x.append(item[0])
    l1.append(item[1])
    l2.append(item[2])
    l3.append(item[3])
    l4.append(item[4])
    l5.append(item[5])
    l6.append(item[6])
    l7.append(item[7])
    l8.append(item[8])
    l9.append(item[9])
    l10.append(item[10])
    i+=1
    if(i>=15):
        break

plt.rcParams['font.sans-serif'] = ['SimHei']  # 用于正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用于正常显示负数

plt.plot(x, l1, 'r', marker='o', markersize=2)
plt.plot(x, l2, 'y', marker='o', markersize=2)
plt.plot(x, l3, 'g', marker='o', markersize=2)
plt.plot(x, l4, 'lightgreen', marker='o', markersize=2)
plt.plot(x, l5, 'b', marker='o', markersize=2)
plt.plot(x, l6, 'purple', marker='o', markersize=2)
plt.plot(x, l7, 'deeppink', marker='o', markersize=2)
plt.plot(x, l8, 'orange', marker='o', markersize=2)
plt.plot(x, l9, 'aqua', marker='o', markersize=2)
plt.plot(x, l10, 'black', marker='o', markersize=2)

plt.xlabel('gene_id',fontsize=20)
plt.title("PAAD癌症类型患者的各基因表达情况(前15个为例）", fontsize=25)

plt.show()

###4.属性相关分析和信息增益

属性相关分析：

简而言之就是把不相关和弱相关的属性去除，保留对数据挖掘任务最相关的属性，然后再进行类特征化和类比较分析。

属性相关分析的基本思想是计算某种度量，用于量化属性与给定类或概念的相关性。

信息增益：

信息增益通过计算一个样本分类的期望信息和属性的熵来获得一个属性的信息增益，判定该属性与当前的特征化任务的相关性。

具有高信息增益的属性，是给定集合中具有高区分度的属性。所以可以通过计算样本的每个属性的信息增益，来得到一个属性的相关性的排序。

信息熵 1948年香农提出了信息熵（Entropy）的概念。

1、从信息的完整性上进行的描述:
当系统的有序状态一致时，数据越集中的地方熵值越小，数据越分散的地方熵值越大。
2、从信息的有序性上进行的描述:
当数据量一致时，系统越有序，熵值越低；系统越混乱或者分散，熵值越高。
“信息熵” (information entropy)是度量样本集合纯度最常用的一种指标。

log都是log2。 Ent(D) 的值越小,则D的纯度越高 。

信息增益以某特征划分数据集前后的熵的差值。熵可以表示样本集合的不确定性，熵越大，样本的不确定性就越大。因此可以使用划分前后集合熵的差值来衡量使用当前特征对于样本集合D划分效果的好坏。
信息增益 = entroy(前) - entroy(后)

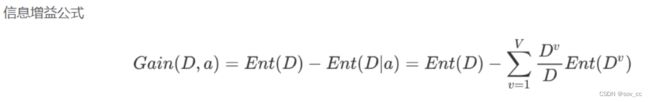
信息增益表示得知特征X的信息而使得类Y的信息的不确定性减少的程度

好的条件就是信息增益越大越好，即变化完后熵越小越好（熵代表混乱程度，最大程度地减小了混乱）。

5.属性相关分析和信息增益-实操

求解在BLCA癌症下，A2BP1|54715和A2ML1|144568两个基因的信息增益。

代码：

import numpy as np
import pandas as pd

# 1. 准备数据
data = pd.read_csv(
    'C:\\Users\\coral\\Desktop\\shujuwajue\\data\\BLCA\\rna.csv',index_col=0)
#index_col=0是为了不产生默认行号

data = data.T

# print(data)
# print(data.groupby("A2BP1|54715"))

#定义计算熵的函数
def ent(data):
    prob1 = pd.value_counts(data) / len(data)
    return sum(np.log2(prob1) * prob1 * (-1))

#定义计算信息增益的函数
def gain(data, str1, str2):
    e1 = data.groupby(str1).apply(lambda x: ent(x[str2]))
    p1 = pd.value_counts(data[str1]) / len(data[str1])
    e2 = sum(e1 * p1)
    print(ent(data[str2]) - e2)
    return ent(data[str2]) - e2

#测试
gain(data, "A2BP1|54715", "A2ML1|144568")

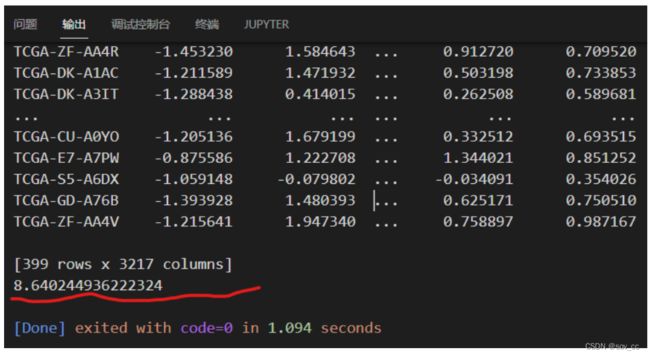
结果：

由公式得到信息增益约为8.64，是很大的数字，说明这两组数据可用性高。

三、参考资料

1.主成分分析

https://www.bilibili.com/video/BV1E5411E71z/

https://blog.csdn.net/weixin_46277779/article/details/125533173

2.类概念描述及特征化分析

https://blog.csdn.net/master_hunter/article/details/126139761

3.信息增益

https://blog.csdn.net/qq_41475067/article/details/113898634

https://blog.csdn.net/spartanfuk/article/details/82052503