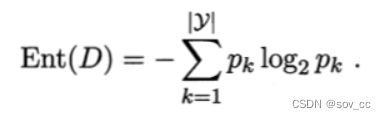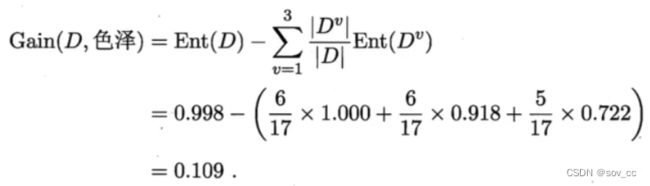用python实现决策树分类-实验报告
数据挖掘实验1.完成时间:2022.11.29。仅供参考
数据源及代码相关文章:用python实现决策树分类-用户手册
实验内容 :
- 了解常见的决策树算法: ID3算法和C4.5
- 熟悉决策树分类的具体步骤和详细过程。
- 对已有的疾病数据实现决策树分类方法。
决策树是一种十分常用的分类方法。它是一种监督学习,所谓监督学习就是给定一堆样本,每个样本都有一组属性和一个类别,这些类别是事先确定的,那么通过学习得到一个分类器,这个分类器能够对新出现的对象给出正确的分类。决策树是一种树形结构,其中每个内部节点表示一个属性上的测试,每个分支代表一个测试输出,每个叶节点代表一种类别。
1、了解常见的决策树算法: ID3算法和C4.5
决策树学习的关键其实就是选择最优划分属性,希望划分后,分支结点的“纯度”越来越高。
那么“纯度”的度量方法不同,也就导致了学习算法的不同,ID3算法与C4.5算法的区分也在于此。
(1)ID3算法
采取信息增益来作为纯度的度量
信息增益是:信息熵-条件熵。
【信息熵是代表随机变量的复杂度(不确定度),条件熵代表在某一个条件下,随机变量的复杂度(不确定度)】
·当前样本集合 D 中第 k 类样本所占的比例为 pk ,则 D 的信息熵定义为
·离散属性 a 有 V 个可能的取值 {a1,a2,…,aV};样本集合中,属性 a 上取值为 av 的样本集合,记为 Dv。
·用属性 a 对样本集 D 进行划分所获得的“信息增益”
如果选择一个特征后,信息增益最大(信息不确定性减少的程度最大),那么我们就选取这个特征。
缺点:
我们从上面求解信息增益的公式中,其实可以看出,信息增益准则其实是对可取值数目较多的属性有所偏好!
现在假如我们把数据集中的“编号”也作为一个候选划分属性。我们可以算出“编号”的信息增益是0.998
因为每一个样本的编号都是不同的(由于编号独特唯一,条件熵为0了,每一个结点中只有一类,纯度非常高啊),也就是说,来了一个预测样本,你只要告诉我编号,其它特征就没有用了,这样生成的决策树显然不具有泛化能力。
(2)C4.5算法
使用了信息增益率来作为纯度的度量
信息增益率的公式:
由上图我们可以看出,信息增益率=信息增益/IV(a),说明信息增益率是信息增益除了一个属性a的固有值得来的。
IV(a)的公式:
当选取该属性,分成的V类别数越大,IV(a)就越大
缺点:
有了这个分母之后,**我们可以看到增益率准则其实对可取类别数目较少的特征有所偏好!**毕竟分母越小,整体越大。
于是C4.5算法不直接选择增益率最大的候选划分属性,候选划分属性中找出信息增益高于平均水平的属性(这样保证了大部分好的的特征),再从中选择增益率最高的(*又保证了不会出现编号特征这种极端的情况*)
2、熟悉决策树分类的具体步骤和详细过程。
概念:
决策树(decision tree)是一个树结构(可以是二叉树或非二叉树)。
其每个非叶节点表示一个特征属性上的测试,每个分支代表这个特征属性在某个值域上的输出,而每个叶节点存放一个类别。
使用决策树进行决策的过程就是从根节点开始,测试待分类项中相应的特征属性,并按照其值选择输出分支,直到到达叶子节点,将叶子节点存放的类别作为决策结果。
总结来说:
决策树模型核心是下面几部分:
- 结点和有向边组成
- 结点有内部结点和叶结点俩种类型
- 内部结点表示一个特征,叶节点表示一个类
决策树表示如下:
步骤
特征选择→决策树生成→剪枝
1、特征选择:特征选择是指从训练数据中众多的特征中选择一个特征作为当前节点的分裂标准,如何选择特征有着很多不同量化评估标准标准,从而衍生出不同的决策树算法,如CART, ID3, C4.5等。
2、决策树生成: 根据选择的特征评估标准,从上至下递归地生成子节点,直到数据集不可分则停止决策树停止生长。 树结构来说,递归结构是最容易理解的方式。
3、剪枝:决策树容易过拟合,一般来需要剪枝,缩小树结构规模、缓解过拟合。剪枝技术有预剪枝和后剪枝两种。
详细过程
以ID3算法为例子构造上述决策树:
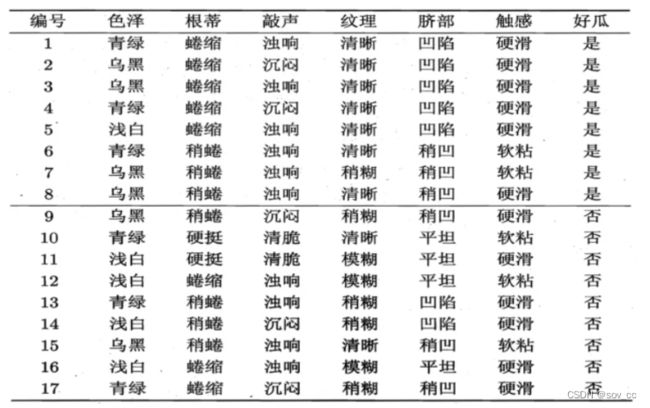
正例(好瓜)占 8/17,反例占 9/17 ,根结点的信息熵为

计算当前属性集合{色泽,根蒂,敲声,纹理,脐部,触感}中每个属性的信息增益
色泽有3个可能的取值:{青绿,乌黑,浅白}
D1(色泽=青绿) = {1, 4, 6, 10, 13, 17},正例 3/6,反例 3/6
D2(色泽=乌黑) = {2, 3, 7, 8, 9, 15},正例 4/6,反例 2/6
D3(色泽=浅白) = {5, 11, 12, 14, 16},正例 1/5,反例 4/5
3 个分支结点的信息熵
那么我们可以知道属性色泽的信息增益是:
同理,我们可以求出其它属性的信息增益,分别如下:
于是我们找到了信息增益最大的属性纹理,它的Gain(D,纹理) = 0.381最大。
于是我们选择的划分属性为“纹理”
如下:
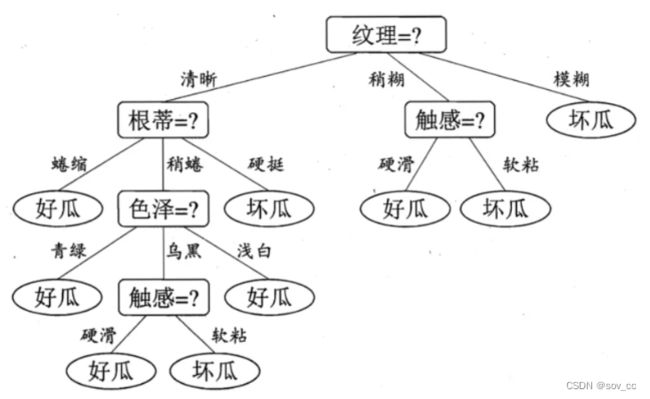
于是,我们可以得到了三个子结点,对于这三个子节点,我们可以递归的使用刚刚找信息增益最大的方法进行选择特征属性,
比如: D1(纹理=清晰) = {1, 2, 3, 4, 5, 6, 8, 10, 15},第一个分支结点可用属性集合{色泽、根蒂、敲声、脐部、触感},基于 D1各属性的信息增益,分别求的如下:
于是我们可以选择特征属性为根蒂,脐部,触感三个特征属性中任选一个(因为他们三个相等并最大),其它俩个子结点同理,然后得到新一层的结点,再递归的由信息增益进行构建树即可
我们最终的决策树如下:
3、对已有的疾病数据实现决策树分类方法
思路:以BLCA和BRCA为例,将二者的样本数据混在一起。根据不同基因的表达情况比如(x<1,1
法一:(对应tree-2.py,用graphviz库。建议)
1、首先导入必要的库
import pandas as pd
from sklearn import tree
import numpy as np
import graphviz
2、将BLCA.csv和BRCA.csv导入、转置。方便后续处理
data1 = pd.read_csv(
'D:\\data_analyze\\data\\BLCA.csv', index_col=0)
#index_col=0表示不生成序号,负责读入时会默认按列生成序号
len1 = data1.shape[1] # 返回列数,后续经常会用到
data1 = data1.T
#先各新增一列kind用于区分是BLCA还是BRCA
name1 = []
for i in range(len1):
name1.append('BLCA')
data1['kind'] = name1
data2 = pd.read_csv(
'D:\\data_analyze\\data\\BRCA.csv', index_col=0)
len2 = data2.shape[1] # 返回列数,后续经常会用到
data2 = data2.T
name2 = []
for i in range(len2):
name2.append('BRCA')
data2['kind'] = name2
3、合并,设置哪个是特征数据,哪个是类别数据
l1 = np.array(data1['kind']) # 特征数据
l2 = np.array(data2['kind'])
labels = np.concatenate([l1, l2], axis=0)
d1 = np.array(data1.iloc[:, :-1]) #类别数据
d2 = np.array(data2.iloc[:, :-1])
data = np.concatenate([d1, d2], axis=0)
4、生成决策树
# 建立决策树分类器参数criterion = 'entropy'为基于信息熵,‘gini’为基于基尼指数
clf = tree.DecisionTreeClassifier(criterion='entropy')
#训练决策树模型
clf.fit(data, labels) # 训练模型
5、可视化到Source.gv.pdf
dot_data = tree.export_graphviz(clf, out_file=None,
feature_names=data1.columns[:-1].values,
class_names=data1.columns[-1],
filled=True, rounded=True,
special_characters=True)
graph = graphviz.Source(dot_data)
graph.view()
class=i的癌症类型为BLCA,class=k的癌症类型为BRCA,成功实现了分类
法二:(对应tree.py,不建议,单独生成.dot文件后再可视化)
前面1-4步与法一相同,第5步可视化有变化。
py代码最后加入下述,表示将上述数据生成tree.dot的文件
with open("tree.dot", 'w') as f:#将构建好的决策树保存到tree.dot文件中
f = tree.export_graphviz(clf,feature_names = np.array(dt1.columns[:-1]), out_file = f)
之后在命令行进入改文件所在路径,使用命令:
dot -Tpng tree.dot -o tree.png
可以生成tree.png。如下,没法直观判断哪个条件是BLCA,哪个是BRCA
##4、其余补充
1、安装好Graphviz后,在VSC内可安装Graphviz Interactive Prev插件,在VSC中打开生成的tree.dot文件。
右侧自动会生成预览(未生成的话,在vsc内部命令面板中运行第一个插件提供的命令 graphviz interactive: preview (beside) )
2、安装Graphviz库的教程
(1)去官网(Graphviz)下载最新稳定版,然后在电脑命令行输入
dot -v
确定已安装
(2)然后,我们需要在python使用时输出我们画的图还需要安装一下graphviz的包
打开Anaconda Prompt(win10在电脑左下方搜索框就能找到) 输入pip install graphviz或者conda install graphviz
如果报错,则选择安装python-graphviz,conda install python-graphviz
(3)在VSC的settings.json文件中添加路径
文件→首选项→设置,点击右上角json
添加下面这句话(记得修改路径到自己安装的位置)
"graphvizPreview.dotPath": "D:\\Graphviz\\bin\\dot.exe"
(4)这个时候就搞定了,可以用下述代码测试(对应test.py)
from graphviz import Digraph
import os
os.environ["PATH"] += os.pathsep + 'D:/Program Files/Graphviz/bin/'
dot = Digraph('测试')
dot.node("1", "Hello")
dot.node("2", "World")
dot.edge('1', '2')
dot.view()
生成
(3)参考资料
前期知识学习:
https://zhuanlan.zhihu.com/p/26703300)
https://zhuanlan.zhihu.com/p/26760551)
https://zhuanlan.zhihu.com/p/42164714
主要参考:
https://blog.csdn.net/ryo007gnnu/article/details/120626255
早期数据处理:
https://blog.csdn.net/qq_40765537/article/details/105869910
https://blog.csdn.net/kanchigo/article/details/117638066
Graphviz库相关:
https://blog.csdn.net/myRealization/article/details/119459490
https://blog.csdn.net/liu_1314521/article/details/115638429
https://blog.csdn.net/NanamiKento/article/details/122748520