机器学习之使用Python生成ID3决策树
文章目录
- ❤❤❤ID3算法
-
- ✅✅决策树的思想:
-
- ID3算法:
- 1.先写绘图树方法,函数。
- 2.ID3决策树类
- 给出数据集,标签集:
- 完整代码
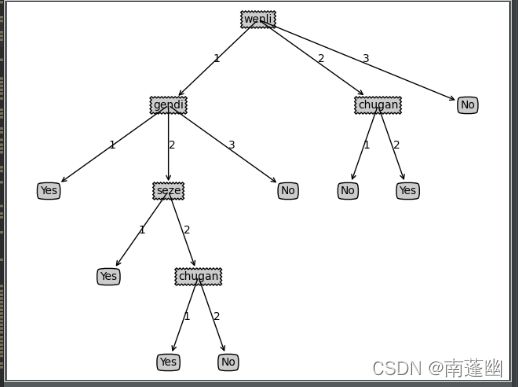
- 生成决策树:
❤❤❤ID3算法
✅✅决策树的思想:
给定一个集合,其中的每个样本由若干属性表示,决策树通过贪心的策略不断挑选最优的属性。
常见的决策树算法有ID3,C4.5,CART算法等。
ID3算法:
baseEntropy = self.calcShannonEnt(dataset) # 基础熵 num = len(dataset) # 样本总数 #子集中的概率 subDataSet = self.splitDataSet(dataset, i, val) prob = len(subDataSet) / float(num) # 条件熵 newEntropy += prob * self.calcShannonEnt(subDataSet) # 信息增益 infoGain = baseEntropy - newEntropy
1.先写绘图树方法,函数。
import matplotlib.pyplot as plt
decisionNode = dict(boxstyle="sawtooth", fc="0.8")
leafNode = dict(boxstyle="round4", fc="0.8")
arrow_args = dict(arrowstyle="<-")
def plotNode(nodeTxt, centerPt, parentPt, nodeType):
createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction', \
xytext=centerPt, textcoords='axes fraction', \
va="center", ha="center", bbox=nodeType, arrowprops=arrow_args)
def getNumLeafs(myTree):
numLeafs = 0
firstStr = list(myTree.keys())[0]
secondDict = myTree[firstStr]
for key in secondDict.keys():
if type(secondDict[key]).__name__ == 'dict':
numLeafs += getNumLeafs(secondDict[key])
else:
numLeafs += 1
return numLeafs
def getTreeDepth(myTree):
maxDepth = 0
firstStr = list(myTree.keys())[0]
secondDict = myTree[firstStr]
for key in secondDict.keys():
if type(secondDict[key]).__name__ == 'dict':
thisDepth = getTreeDepth(secondDict[key]) + 1
else:
thisDepth = 1
if thisDepth > maxDepth:
maxDepth = thisDepth
return maxDepth
def plotMidText(cntrPt, parentPt, txtString):
xMid = (parentPt[0] - cntrPt[0]) / 2.0 + cntrPt[0]
yMid = (parentPt[1] - cntrPt[1]) / 2.0 + cntrPt[1]
createPlot.ax1.text(xMid, yMid, txtString)
def plotTree(myTree, parentPt, nodeTxt):
numLeafs = getNumLeafs(myTree)
depth = getTreeDepth(myTree)
firstStr = list(myTree.keys())[0]
cntrPt = (plotTree.xOff + (1.0 + float(numLeafs)) / 2.0 / plotTree.totalw, plotTree.yOff)
plotMidText(cntrPt, parentPt, nodeTxt)
plotNode(firstStr, cntrPt, parentPt, decisionNode)
secondDict = myTree[firstStr]
plotTree.yOff = plotTree.yOff - 1.0 / plotTree.totalD
for key in secondDict.keys():
if type(secondDict[key]).__name__ == 'dict':
plotTree(secondDict[key], cntrPt, str(key))
else:
plotTree.xOff = plotTree.xOff + 1.0 / plotTree.totalw
plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)
plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))
plotTree.yOff = plotTree.yOff + 1.0 / plotTree.totalD
def createPlot(inTree):
fig = plt.figure(1, facecolor='white')
fig.clf()
axprops = dict(xticks=[], yticks=[])
createPlot.ax1 = plt.subplot(111, frameon=False, **axprops)
plotTree.totalw = float(getNumLeafs(inTree))
plotTree.totalD = float(getTreeDepth(inTree))
plotTree.xOff = -0.5 / plotTree.totalw
plotTree.yOff = 1.0
plotTree(inTree, (0.5, 1.0), '')
plt.show()
2.ID3决策树类
class ID3Tree(object):
def __init__(self):
self.tree = {} # ID3 Tree
self.dataSet = [] # 数据集
self.labels = [] # 标签集
def getDataSet(self, dataset, labels):
self.dataSet = dataset
self.labels = labels
def train(self):
# labels = copy.deepcopy(self.labels)
labels = self.labels[:]
self.tree = self.buildTree(self.dataSet, labels)
def buildTree(self, dataSet, labels):
classList = [ds[-1] for ds in dataSet] # 提取样本的类别
if classList.count(classList[0]) == len(classList): # 单一类别
return classList[0]
if len(dataSet[0]) == 1: # 没有属性需要划分了
return self.classify(classList)
bestFeat = self.findBestSplit(dataSet) # 选取最大增益的属性序号
bestFeatLabel = labels[bestFeat]
tree = {bestFeatLabel: {}} # 构造一个新的树结点
del (labels[bestFeat]) # 从总属性列表中去除最大增益属性
featValues = [ds[bestFeat] for ds in dataSet] # 抽取最大增益属性的取值列表
uniqueFeatValues = set(featValues) # 选取最大增益属性的数值类别
for value in uniqueFeatValues: # 对于每一个属性类别
subLabels = labels[:]
subDataSet = self.splitDataSet(dataSet, bestFeat, value) # 分裂结点
subTree = self.buildTree(subDataSet, subLabels) # 递归构造子树
tree[bestFeatLabel][value] = subTree
return tree
# 计算出现次数最多的类别标签
def classify(self, classList):
items = dict([(classList.count(i), i) for i in classList])
return items[max(items.keys())]
# 计算最优特征
def findBestSplit(self, dataset):
numFeatures = len(dataset[0]) - 1
baseEntropy = self.calcShannonEnt(dataset) # 基础熵
num = len(dataset) # 样本总数
bestInfoGain = 0.0
bestFeat = -1 # 初始化最优特征向量轴
# 遍历数据集各列,寻找最优特征轴
for i in range(numFeatures):
featValues = [ds[i] for ds in dataset]
uniqueFeatValues = set(featValues)
newEntropy = 0.0
# 按列和唯一值,计算信息熵
for val in uniqueFeatValues:
subDataSet = self.splitDataSet(dataset, i, val)
prob = len(subDataSet) / float(num) # 子集中的概率
newEntropy += prob * self.calcShannonEnt(subDataSet)
infoGain = baseEntropy - newEntropy # 信息增益
if infoGain > bestInfoGain: # 挑选最大值
bestInfoGain = baseEntropy - newEntropy
bestFeat = i
return bestFeat
# 从dataset数据集的feat特征中,选取值为value的数据
def splitDataSet(self, dataset, feat, values):
retDataSet = []
for featVec in dataset:
if featVec[feat] == values:
reducedFeatVec = featVec[:feat]
reducedFeatVec.extend(featVec[feat + 1:])
retDataSet.append(reducedFeatVec)
return retDataSet
# 计算dataSet的信息熵
def calcShannonEnt(self, dataSet):
num = len(dataSet) # 样本集总数
classList = [c[-1] for c in dataSet] # 抽取分类信息
labelCounts = {}
for cs in set(classList): # 对每个分类进行计数
labelCounts[cs] = classList.count(cs)
shannonEnt = 0.0
for key in labelCounts:
prob = labelCounts[key] / float(num)
shannonEnt -= prob * log2(prob)
return shannonEnt
# 预测。对输入对象进行ID3分类
def predict(self, tree, newObject):
# 判断输入值是否为“dict”
while type(tree).__name__ == 'dict':
key = list(tree.keys())[0]
tree = tree[key][newObject[key]]
return tree
给出数据集,标签集:
dataSet = [[1, 1, 1, 1,1, 1, ‘Yes’],
[2, 1, 2, 1,1, 1, ‘Yes’],
[2, 1, 1, 1,1, 1, ‘Yes’],
[1, 1, 2, 1,1, 1, ‘Yes’],
[3, 1, 1, 1,1, 1, ‘Yes’],
[1,2, 1, 1,2, 2, ‘Yes’],
[2, 2, 1, 2,2, 2, ‘Yes’],
[2, 2, 1, 1,2, 1, ‘Yes’],
[2, 2, 2, 2,2, 1, ‘No’],
[1,3, 3, 1,3, 2, ‘No’],
[3, 3, 3, 3,3, 1, ‘No’],
[3, 1, 1, 3,3, 2, ‘No’],
[1, 2, 1, 2,1, 1, ‘No’],
[3,2, 2, 2,1, 1, ‘No’],
[2, 2, 1, 1,2, 2, ‘No’],
[3, 1, 1, 3,3, 1, ‘No’],
[1, 1, 2, 2,2, 1, ‘No’],]
#'色泽', '根蒂', '敲声', '纹理','脐部', '触感'
features = ['seze', 'gendi', 'qiaosheng', 'wenli','qibu', 'chugan']
完整代码
from math import log2
import treePlotter
class ID3Tree(object):
def __init__(self):
self.tree = {} # ID3 Tree
self.dataSet = [] # 数据集
self.labels = [] # 标签集
def getDataSet(self, dataset, labels):
self.dataSet = dataset
self.labels = labels
def train(self):
# labels = copy.deepcopy(self.labels)
labels = self.labels[:]
self.tree = self.buildTree(self.dataSet, labels)
def buildTree(self, dataSet, labels):
classList = [ds[-1] for ds in dataSet] # 提取样本的类别
if classList.count(classList[0]) == len(classList): # 单一类别
return classList[0]
if len(dataSet[0]) == 1: # 没有属性需要划分了
return self.classify(classList)
bestFeat = self.findBestSplit(dataSet) # 选取最大增益的属性序号
bestFeatLabel = labels[bestFeat]
tree = {bestFeatLabel: {}} # 构造一个新的树结点
del (labels[bestFeat]) # 从总属性列表中去除最大增益属性
featValues = [ds[bestFeat] for ds in dataSet] # 抽取最大增益属性的取值列表
uniqueFeatValues = set(featValues) # 选取最大增益属性的数值类别
for value in uniqueFeatValues: # 对于每一个属性类别
subLabels = labels[:]
subDataSet = self.splitDataSet(dataSet, bestFeat, value) # 分裂结点
subTree = self.buildTree(subDataSet, subLabels) # 递归构造子树
tree[bestFeatLabel][value] = subTree
return tree
# 计算出现次数最多的类别标签
def classify(self, classList):
items = dict([(classList.count(i), i) for i in classList])
return items[max(items.keys())]
# 计算最优特征
def findBestSplit(self, dataset):
numFeatures = len(dataset[0]) - 1
baseEntropy = self.calcShannonEnt(dataset) # 基础熵
num = len(dataset) # 样本总数
bestInfoGain = 0.0
bestFeat = -1 # 初始化最优特征向量轴
# 遍历数据集各列,寻找最优特征轴
for i in range(numFeatures):
featValues = [ds[i] for ds in dataset]
uniqueFeatValues = set(featValues)
newEntropy = 0.0
# 按列和唯一值,计算信息熵
for val in uniqueFeatValues:
subDataSet = self.splitDataSet(dataset, i, val)
prob = len(subDataSet) / float(num) # 子集中的概率
newEntropy += prob * self.calcShannonEnt(subDataSet)
infoGain = baseEntropy - newEntropy # 信息增益
if infoGain > bestInfoGain: # 挑选最大值
bestInfoGain = baseEntropy - newEntropy
bestFeat = i
return bestFeat
# 从dataset数据集的feat特征中,选取值为value的数据
def splitDataSet(self, dataset, feat, values):
retDataSet = []
for featVec in dataset:
if featVec[feat] == values:
reducedFeatVec = featVec[:feat]
reducedFeatVec.extend(featVec[feat + 1:])
retDataSet.append(reducedFeatVec)
return retDataSet
# 计算dataSet的信息熵
def calcShannonEnt(self, dataSet):
num = len(dataSet) # 样本集总数
classList = [c[-1] for c in dataSet] # 抽取分类信息
labelCounts = {}
for cs in set(classList): # 对每个分类进行计数
labelCounts[cs] = classList.count(cs)
shannonEnt = 0.0
for key in labelCounts:
prob = labelCounts[key] / float(num)
shannonEnt -= prob * log2(prob)
return shannonEnt
# 预测。对输入对象进行ID3分类
def predict(self, tree, newObject):
# 判断输入值是否为“dict”
while type(tree).__name__ == 'dict':
key = list(tree.keys())[0]
tree = tree[key][newObject[key]]
return tree
if __name__ == '__main__':
def createDataSet():
dataSet = [[1, 1, 1, 1,1, 1, 'Yes'],
[2, 1, 2, 1,1, 1, 'Yes'],
[2, 1, 1, 1,1, 1, 'Yes'],
[1, 1, 2, 1,1, 1, 'Yes'],
[3, 1, 1, 1,1, 1, 'Yes'],
[1,2, 1, 1,2, 2, 'Yes'],
[2, 2, 1, 2,2, 2, 'Yes'],
[2, 2, 1, 1,2, 1, 'Yes'],
[2, 2, 2, 2,2, 1, 'No'],
[1,3, 3, 1,3, 2, 'No'],
[3, 3, 3, 3,3, 1, 'No'],
[3, 1, 1, 3,3, 2, 'No'],
[1, 2, 1, 2,1, 1, 'No'],
[3,2, 2, 2,1, 1, 'No'],
[2, 2, 1, 1,2, 2, 'No'],
[3, 1, 1, 3,3, 1, 'No'],
[1, 1, 2, 2,2, 1, 'No'],]
#'色泽', '根蒂', '敲声', '纹理','脐部', '触感'
features = ['seze', 'gendi', 'qiaosheng', 'wenli','qibu', 'chugan']
return dataSet, features
id3 = ID3Tree() # 创建一个ID3决策树
ds, labels = createDataSet()
id3.getDataSet(ds, labels)
id3.train() # 训练ID3决策树
print(id3.tree) # 输出ID3决策树
print(id3.predict(id3.tree,{'seze':2,'gendi':2,'qiaosheng':1,'wenli':1,'qibu':1,'chugan':1}))
treePlotter.createPlot(id3.tree)