无监督算法
无监督算法简介
就是依靠数据之间的相似度,形成数据的类别。(下图有些是网上扒的,如有侵权望告知,立删)
层次聚类
比如有7个数据点,A,B,C,D,E,F,G。我们采用数据的欧式距离作为相似度(距离越小越相似):
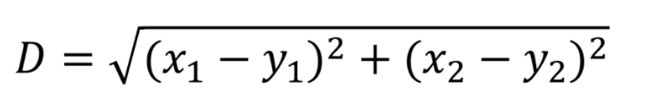
将数据分别两两计算相似度:

得到BC的距离最小,这样我们就得到一个新的集合或者说是类:(B,C)。这样我们下一次计算相似度时,只有6个元素了:A,(B,C),D,E,F,G。然后两两计算相似度,得到:
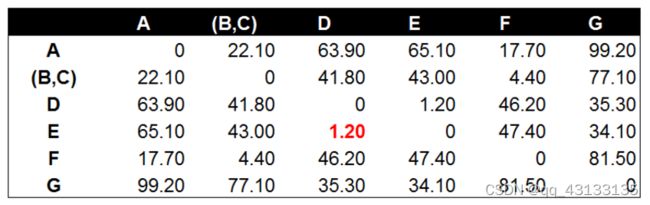
当然,要提到的一点是,对于任意元素(如A)和集合(B,C)之间的距离度量,则取A分别和B,C的距离的均值(下面是几何均值):
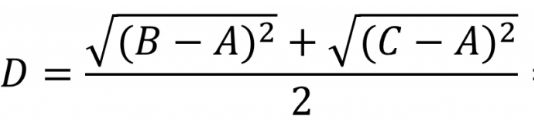
当然若是两个类(A,F)和(B,C)的距离,则取两两间距离的均值:
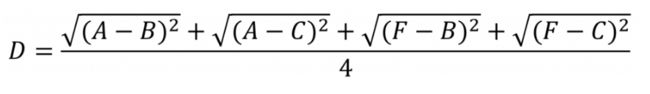
当然集合之间的距离有很多种取法,不局限于上述,如:
1、取两个类中距离最小的两个样本的距离作为两个集合的距离
2、取两个类中距离最大的两个样本的距离作为两个集合的距离
3、计算两个集合中每两两点的距离并取平均值
最后便可以形成如下聚类图(我随便画的):
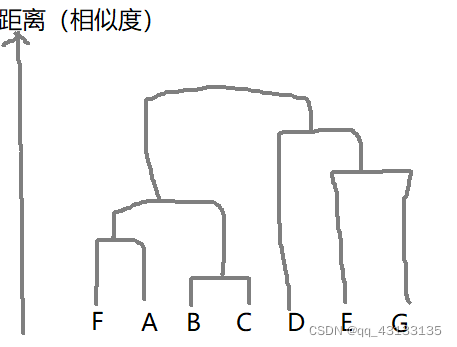
如果你的目标是分成3类,只需要拿一条横线截一下上面的图,让横线只穿过3条竖线即可。
K-Means
将数据分为k个簇 { C 1 , C 2 , ⋯ , C k } \{C_1,C_2,⋯,C_k\} {C1,C2,⋯,Ck},每个簇有一个中心 μ i \mu_i μi。
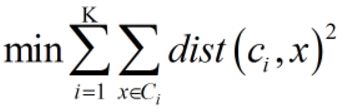
常用的相似度度量有欧几里得距离和余弦相似度。以下以距离为例:
首先随便取k个中心,然后分别计算每个点到各个中心的距离,离哪个中心近,就把它归到哪个中心
然后根据各中心包含的点,重新计算中心位置,然后重新对各点进行中心归类。一直迭代,直到中心不再变化为止。
均值漂移(Mean Shift)
漂移向量是给定中心点 X c X_c Xc距离小于 h h h的数据点集均值:
M h = E x i ∈ ( D < h ) [ x i − x c ] M_h =E_{x_i∈ (D
该向量表明了该范围内的数据实际中心与给定中心的偏差。然后进行中心位置更新(即漂移操作)
x c ← x c + M h x_c ← x_c + M_h xc←xc+Mh 。
重复进行迭代,直到收敛。
当然,是每次从未被标记(未分类)的数据中随意选一个点作为中心点,然后进行上述迭代,直到收敛。最后得到n个中心。
n个中心中,若两个中心距离小于h则进行合并,其数据归为一大类。若中心距离大于h且小于2h,即范围发生了重叠,则重叠部分可按照最近的中心进行分类,或者采用核函数看贡献值。
更多可参考:机器学习聚类算法之Mean Shift
DBSCAN密度聚类
基本概念
假定同一类别的样本,他们之间的紧密相连的。
使用参数 ( ϵ , M i n P t s ) (ϵ, MinPts) (ϵ,MinPts)用来描述邻域的样本分布紧密程度。其中,ϵ描述了某一样本的邻域距离阈值,MinPts描述了邻域中样本个数的阈值。
假设样本集是 D = ( x 1 , x 2 , . . . , x m ) D=(x_1,x_2,...,x_m) D=(x1,x2,...,xm),则对于 x j ∈ D x_j∈D xj∈D有:
ϵ-邻域:其ϵ-邻域包含样本集 N ϵ ( x j ) = x i ∈ D ∣ d i s t a n c e ( x i , x j ) ≤ ϵ Nϵ(x_j)={xi∈D|distance(x_i,x_j)≤ϵ} Nϵ(xj)=xi∈D∣distance(xi,xj)≤ϵ,且 个数记为 ∣ N ϵ ( x j ) ∣ |Nϵ(x_j)| ∣Nϵ(xj)∣
核心对象:如果其ϵ-邻域对应的 ∣ N ϵ ( x j ) ∣ ≥ M i n P t s |Nϵ(x_j)|≥MinPts ∣Nϵ(xj)∣≥MinPts,则其为核心对象。
密度直达:如果 x j x_j xj是核心对象,且 x i x_i xi位于 x j x_j xj的ϵ-邻域中,则称 x i x_i xi由 x j x_j xj密度直达。
密度可达:如果存在样本序列 p 1 , p 2 , . . . , p t p_1,p_2,...,p_t p1,p2,...,pt, 且 p t + 1 p_{t+1} pt+1由 p t p_t pt密度直达。若满足 p 1 p_1 p1= x i x_i xi, p t p_t pt= x j x_j xj, 则称 x j x_j xj由 x i x_i xi密度可达。也就是说,密度可达满足传递性。
(此时序列中的传递样本 p 1 , p 2 , . . . , p t − 1 p_1,p_2,...,p_{t-1} p1,p2,...,pt−1均为核心对象,因为只有核心对象才能使其他样本密度直达。)
密度相连:对于 x i x_i xi和 x j x_j xj,如果存在核心对象样本 x k x_k xk,使 x i x_i xi和 x j x_j xj均由 x k x_k xk密度可达,则称 x i x_i xi和 x j x_j xj密度相连。
下图中MinPts=5,则红色的点都是核心对象,黑色的样本是非核心对象。所有核心对象密度直达的样本在以红色核心对象为中心的超球体内,不在超球体内则不能密度直达。图中用绿色箭头连起来的核心对象组成了密度可达的样本序列。在这些密度可达的样本序列的ϵ-邻域内所有的样本相互都是密度相连的。

算法思想
1、任意选择一个没有类别的核心对象作为种子,然后找到所有这个核心对象能够密度可达的样本集合,即为一个聚类簇。
2、继续选择另一个没有类别的核心对象去寻找密度可达的样本集合,这样就得到另一个聚类簇。一直运行到所有核心对象都有类别为止,剩下的非核心对象则为噪声点。
某些样本可能到两个核心对象的距离都小于ϵ,但是这两个核心对象由于不是密度直达,又不属于同一个聚类簇,那么如何界定这个样本的类别呢?一般来说,此时DBSCAN采用先来后到,先进行聚类的类别簇会标记这个样本为它的类别。也就是说DBSCAN的算法不是完全稳定的算法。
些异常样本点或者说少量游离于簇外的样本点,这些点不在任何一个核心对象在周围,在DBSCAN中,我们一般将这些样本点标记为噪音点。
更多参考:
具有噪声的基于密度的聚类方法
机器学习–聚类系列–DBSCAN算法(有图)