【机器学习100天】Day25-决策树

代码

数据集地址（点此获取）

# 导入所需的库
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

# 导入数据集
dataset = pd.read_csv(r'D:\Python\100-Days-Of-ML-Code-master\datasets\Social_Network_Ads.csv')
X = dataset.iloc[:, [2, 3]].values
Y = dataset.iloc[:, 4].values

# 将数据集划分为训练集和测试集
from sklearn.model_selection import train_test_split
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.25, random_state=0)

# 特征缩放
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)

# 将决策树分类器拟合到训练集
from sklearn.tree import DecisionTreeClassifier
classifier = DecisionTreeClassifier(criterion='entropy', random_state=0)
classifier.fit(X_train, Y_train)

# 预测测试集
Y_pred = classifier.predict(X_test)

# 生成混淆矩阵
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(Y_test, Y_pred)

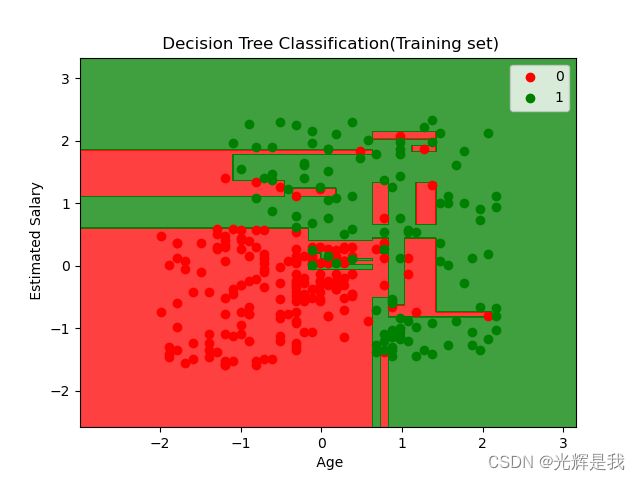
# 可视化训练集结果
from matplotlib.colors import ListedColormap
X_set, Y_set = X_train, Y_train
X1, X2 = np.meshgrid(np.arange(start=X_set[:, 0].min()-1, stop=X_set[:, 0].max()+1, step=0.01),
                     np.arange(start=X_set[:, 1].min()-1, stop=X_set[:, 1].max()+1, step=0.01))
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
             alpha=0.75, cmap=ListedColormap(('red', 'green')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(Y_set)):
    plt.scatter(X_set[Y_set == j, 0], X_set[Y_set == j, 1],
                c=ListedColormap(('red', 'green'))(i), label=j)

plt.title(' Decision Tree Classification(Training set)')
plt.xlabel(' Age')
plt.ylabel(' Estimated Salary')
plt.legend()
plt.show()

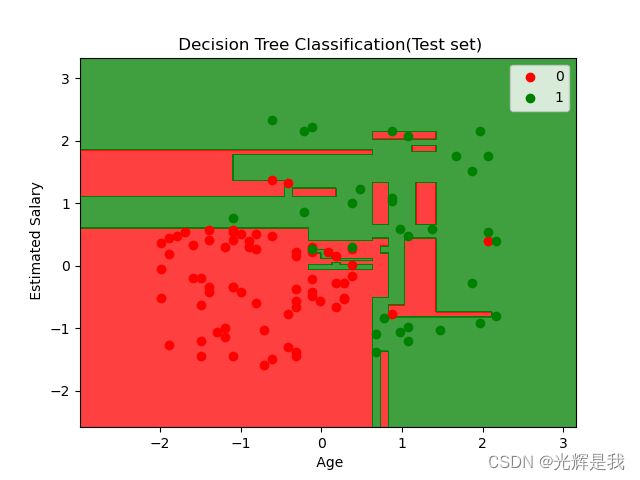
# 可视化测试集结果
X_set, Y_set = X_test, Y_test
X1, X2 = np.meshgrid(np.arange(start=X_set[:, 0].min()-1, stop=X_set[:, 0].max()+1, step=0.01),
                     np.arange(start=X_set[:, 1].min()-1, stop=X_set[:, 1].max()+1, step=0.01))
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
             alpha=0.75, cmap=ListedColormap(('red', 'green')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(Y_set)):
    plt.scatter(X_set[Y_set == j, 0], X_set[Y_set == j, 1],
                c=ListedColormap(('red', 'green'))(i), label=j)

plt.title(' Decision Tree Classification(Test set)')
plt.xlabel(' Age')
plt.ylabel(' Estimated Salary')
plt.legend()
plt.show()

运行结果：

学习

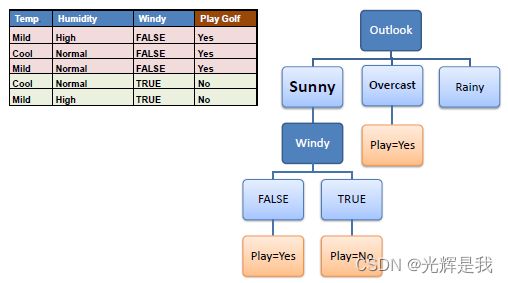
决策树 - 分类 [转载(点击此处获取原文)]

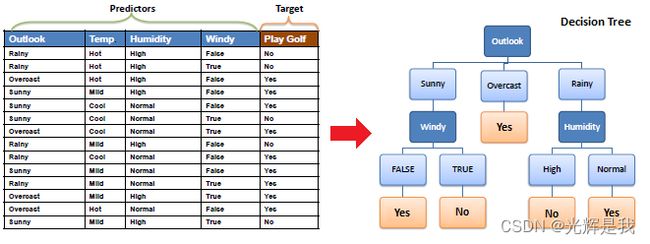
决策树以树结构的形式构建分类或回归模型。它将数据集分解为越来越小的子集，同时逐步开发相关的决策树。最终结果是一棵具有决策节点和叶节点的树。一个决策节点（例如 Outlook）具有两个或多个分支（例如 Sunny、Overcast 和 Rainy）。叶节点（例如，Play）表示分类或决策。树中最顶层的决策节点，对应于称为根节点的最佳预测器。决策树可以处理分类数据和数值数据。

算法

用于构建决策树的核心算法称为ID3，由 JR Quinlan 提出，它在可能的分支空间中采用自上而下的贪婪搜索，无需回溯。ID3 使用熵和信息增益来构建决策树。在ZeroR 模型中没有预测器，在 OneR 模型中我们试图找到单个最佳预测器，朴素贝叶斯包括使用贝叶斯规则和预测器之间的独立假设的所有预测器，但决策树包括具有预测器之间依赖假设的所有预测器。

熵

决策树是从根节点自上而下构建的，涉及将数据划分为包含具有相似值（同质）实例的子集。ID3 算法使用熵来计算样本的同质性。如果样本是完全均匀的，则熵为零，如果样本是均分的，则熵为 1。

为了构建决策树，我们需要使用频率表计算两种类型的熵，如下所示：

a) 使用一个属性的频率表的熵：

b) 熵使用两个属性的频率表：

信息增益

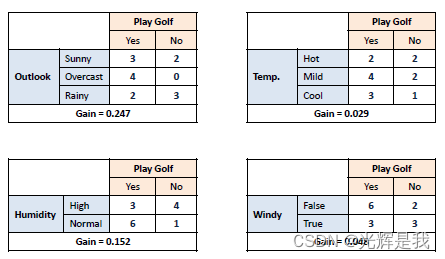
信息增益基于数据集在属性上拆分后熵的减少。构建决策树就是要找到返回最高信息增益的属性（即最同质的分支）。

算法步骤：

步骤 1 ：计算目标的熵。

步骤 2 ：然后根据不同的属性拆分数据集。计算每个分支的熵。然后按比例添加，以获得拆分的总熵。从分裂前的熵中减去得到的熵。结果是信息增益，或熵减少。

步骤 3 ：选择信息增益最大的属性作为决策节点，将数据集除以它的分支，并在每个分支上重复相同的过程。

步骤 4a ：熵为 0 的分支是叶节点。

步骤 4b ：熵大于 0 的分支需要进一步分裂。

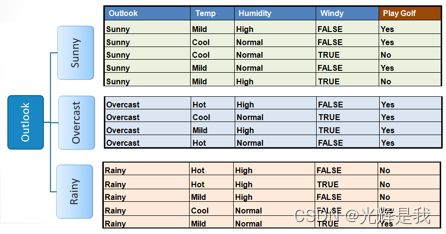
步骤 5 ：在非叶分支上递归运行 ID3 算法，直到所有数据都被分类。

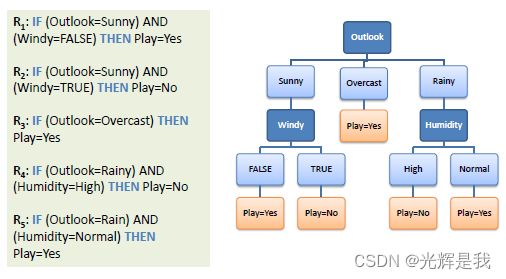
决策树到决策规则

通过从根节点到叶节点的逐一映射，可以轻松地将决策树转换为一组规则。