python实现次梯度(subgradient)和近端梯度下降法 (proximal gradient descent)方法求解L1正则化
l1范数最小化
考虑函数
，显然其在零点不可微，其对应的的次微分为：
![\begin{equation} g = A^T(Ax - b) + \mu \left\{ \begin{array}{lr} 1, & x >0 \\ \left [ -1,1 \right ], & x =0 \\ -1, & x < 0 \end{array} \right. \end{equation}](http://img.e-com-net.com/image/info8/ab7be9a4e5bd4ba5b2a996759018b3cd.gif)
注意
，
的取值为一个区间![\left [ -1, 1 \right ]](http://img.e-com-net.com/image/info8/5cca78eb8fd341df8ef8540b53a8e42b.gif){kind=small}
。
两个重要定理：
1）一个凸函数，当且仅当
，
为全局最小值，即 为最小值点 
；
2）为函数
（不一定是凸函数）的最小值点，当且仅当在该点可次微分且。
考虑最简单的一种情况，目标函数为：
对应的次微分为：
进一步可以表示为：
故，若
，最小值点
为：
若
，最小值点为：
若
， 最小值点为：
简而言之，最优解
，
通常被称为软阈值（soft threshold）算子。
次梯度(subgradient)求解L1正则化问题
考虑最小化问题：
随机生成矩阵
和向量
，
，
，仅、
、为已知量，
为参数。
那么次梯度为：
对于次梯度求解方法，次梯度
可以进一步表示为：
进一步，可以得到次梯度的更新公式为：
python代码如下：
# -*- coding: utf-8 -*-
import numpy as np
import scipy as spy
from scipy.sparse import csc_matrix
import matplotlib.pyplot as plt
import time #用来计算运行时间
#=======模拟数据======================
m = 512
n = 1024
#稀疏矩阵的产生，A使用的是正态稀疏矩阵
u= spy.sparse.rand(n,1,density=0.1,format='csc',dtype=None)
u1 = u.nonzero()
row = u1[0]
col = u1[1]
data = np.random.randn(int(0.1*n))
u = csc_matrix((data, (row, col)), shape=(n,1)).toarray() #1024 * 1
#u1 = u.nonzero() #观察是否是正态分布
#plt.hist(u[u1[0],u1[1]].tolist())
#u = u.todense() #转为非稀疏形式
a = np.random.randn(m,n) #512 * 1024
b = np.dot(a,u) # a * u, 512 * 1
v = 1e-3 #v为题目里面的miu
def f(x0): #目标函数 1/2*||Ax - b||^2 + mu*||x||1
return 1/2*np.dot((np.dot(a,x0)-b).T,np.dot(a,x0)-b)+v*sum(abs(x0))
#==========初始值=============================
x0 = np.zeros((n,1)) #1024 * 1
y = []
time1 = []
start = time.clock()
print("begin to train!")
#=========开始迭代==========================
for i in range(1000):
if i %100 == 0:
if len(y) > 0:
print("step " + str(i) + "val: " + str(y[len(y) - 1]))
mid_result = f(x0)
y.append(f(x0)[0,0]) #存放每次的迭代函数值
g0 = (np.dot(np.dot(a.T,a),x0)-np.dot(a.T,b) + v*np.sign(x0))
#次梯度, A^T(Ax - b) + mu * sign(x)
t = 0.01/np.sqrt(sum(np.dot(g0.T,g0))) #设为0.01效果比0.1好很多，步长
x1 = x0 - t[0]*g0
x0 = x1
end = time.clock()
time1.append(end)
y = np.array(y).reshape((1000,1))
time1 = np.array(time1)
time1 = time1 - start
time2 = time1[np.where(y - y[999] < 10e-4)[0][0]]
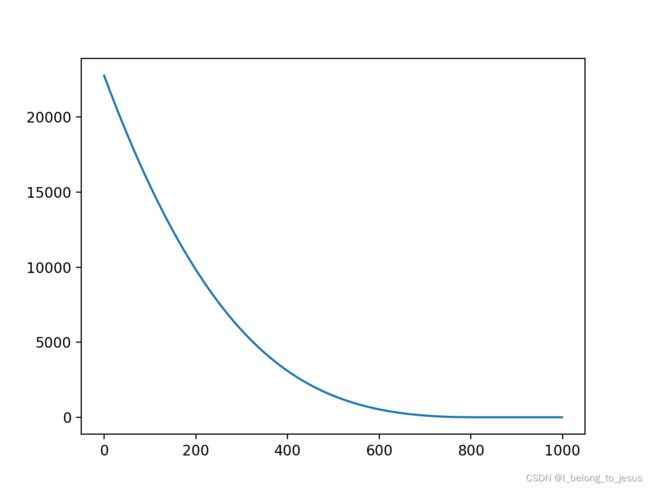
plt.plot(y)
plt.show()
for val in y:
print(val)
# if i % 100 == 0:
# f = 1/2*np.dot((np.dot(a,x0)-b).T,np.dot(a,x0)-b)+v*sum(abs(x0))
# print(f)
#在计算机计算时，可以明显感受到proximal gradient方法比次梯度方法快结果如下：
前几个参数值：
可以看到参数具有稀疏性。
近端梯度下降法 (proximal gradient descent)方法求解L1正则化
proximal gradient算法推导
对于梯度下降的每一步，可以看做是一个平方模型的局部最小化：
其中，
为合适的步长，那么，同理对于有L1正则项的情况，上式变为：
考虑前面介绍的soft threshold，利用soft threshold的方法，我们可以马上得到最优解：
对与上面的例子，我们可以得到基于此方法的梯度更新公式为：
这就是通常所说的Iterative Shrinkage Thresholding Algorithm (ISTA)算法，与subgradient算法相比，由于soft threshold的限制，使得参数的稀疏性更强
相应的python代码为：
# -*- coding: utf-8 -*-
import numpy as np
import scipy as spy
from scipy.sparse import csc_matrix
import matplotlib.pyplot as plt
import time #用来计算运行时间
#=======模拟数据======================
m = 512
n = 1024
#稀疏矩阵的产生，A使用的是正态稀疏矩阵
u= spy.sparse.rand(n,1,density=0.1,format='csc',dtype=None)
u1 = u.nonzero()
row = u1[0]
col = u1[1]
data = np.random.randn(int(0.1*n))
u = csc_matrix((data, (row, col)), shape=(n,1)).toarray() #1024 * 1
#u1 = u.nonzero() #观察是否是正态分布
#plt.hist(u[u1[0],u1[1]].tolist())
#u = u.todense() #转为非稀疏形式
a = np.random.randn(m,n) #512 * 1024
b = np.dot(a,u) # a * u, 512 * 1
v = 1e-3 #v为题目里面的miu
def f(x0): #目标函数 1/2*||Ax - b||^2 + mu*||x||1
return 1/2*np.dot((np.dot(a,x0)-b).T,np.dot(a,x0)-b)+v*sum(abs(x0))
def S(x1,v):
for i in range(len(x1)):
if np.abs(x1[i]) - v > 0:
x1[i] = np.sign(x1[i]) * (np.abs(x1[i]) - v)
else:
x1[i] = 0
return x1
#==========初始值=============================
#x0 = np.zeros((n,1)) #1024 * 1
x0 = (2.0*np.random.random((n,1)) - 1.0) * 0.01
y = []
time1 = []
start = time.clock()
print("begin to train!")
#=========开始迭代==========================
for i in range(2000):
if i %10 == 0:
if len(y) > 0:
print("step " + str(i) + "val: " + str(y[len(y) - 1]))
mid_result = f(x0)
y.append(f(x0)[0,0]) #存放每次的迭代函数值
#g0 = (np.dot(np.dot(a.T,a),x0)-np.dot(a.T,b) + v*np.sign(x0))
#次梯度, A^T(Ax - b) + mu * sign(x)
g0 = np.dot(np.dot(a.T,a),x0)-np.dot(a.T,b)
t = 0.025/np.sqrt(sum(np.dot(g0.T,g0))) #设为0.01效果比0.1好很多，步长
x1 = S(x0 - t[0]*g0, v)
x0 = x1
end = time.clock()
time1.append(end)
y = np.array(y).reshape((2000,1))
time1 = np.array(time1)
time1 = time1 - start
time2 = time1[np.where(y - y[999] < 10e-4)[0][0]]
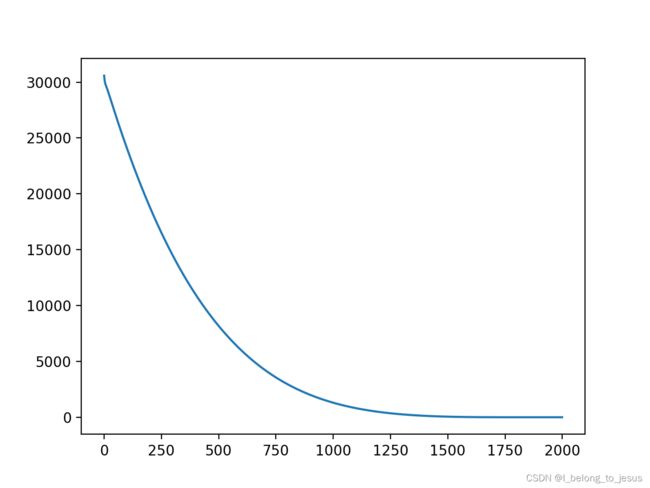
plt.plot(y)
plt.show()
for val in y:
print(val)
# if i % 100 == 0:
# f = 1/2*np.dot((np.dot(a,x0)-b).T,np.dot(a,x0)-b)+v*sum(abs(x0))
# print(f)
#在计算机计算时，可以明显感受到proximal gradient方法比次梯度方法快 
前几个参数如下：
显然与基础次梯度算法相比，此方法稀疏性明显更好。