MATLAB编写自己的BP神经网络程序

 

目录

前言

一、什么是神经网络？

二、手写代码

1.主代码

2.归一化函数

2.反归一化函数

二、工具箱代码

总结

 

---

前言

因为项目需要，自己搞了一个BP神经网络的程序，顺便做一下笔记

人工智能现在的分支有

 1机器学习：就是通过算法从大数据中学习到规律，而后对未知的结果进行预测。

   1.21监督学习：输入和输出已知，训练集中的目标是人为注入的，常见的作用是分类数据。回归分析，统计分类。

    1.22 非监督学习：事先没有样本，直接对数据进行建模，非监督学习最点典型的例子就是聚类。

    1.23 半监督学习 ：事先样本有的又标签有的没有标签，能够生成又监督的分类算法。

2 深度学习

  2.1卷积神经网络

  2.2循环神经网络

3神经网络 也是人工智能的一个分支

     相比与是一种浅度学习

一、什么是神经网络？

  人工神经网络（英语：Artificial Neural Network，ANN），简称神经网络（Neural Network，NN）或类神经网络，在机器学习和认知科学领域，是一种模仿生物神经网络（动物的中枢神经系统，特别是大脑）的结构和功能的数学模型或计算模型，用于对函数进行估计或近似。神经网络由大量的人工神经元联结进行计算。大多数情况下人工神经网络能在外界信息的基础上改变内部结构，是一种自适应系统，通俗的讲就是具备学习功能。现代神经网络是一种非线性统计性数据建模工具，神经网络通常是通过一个基于数学统计学类型的学习方法（Learning Method）得以优化，所以也是数学统计学方法的一种实际应用，通过统计学的标准数学方法我们能够得到大量的可以用函数来表达的局部结构空间，另一方面在人工智能学的人工感知领域，我们通过数学统计学的应用可以来做人工感知方面的决定问题（也就是说通过统计学的方法，人工神经网络能够类似人一样具有简单的决定能力和简单的判断能力），这种方法比起正式的逻辑学推理演算更具有优势。

 

 人工神经元模型

它的通俗理解就是输入：变量分别和对应的权重(学名叫连接权值)的乘积记为，在通过一个f(out)输出及得到一个对应输入的输出值。（f（out）学名叫激活函数）

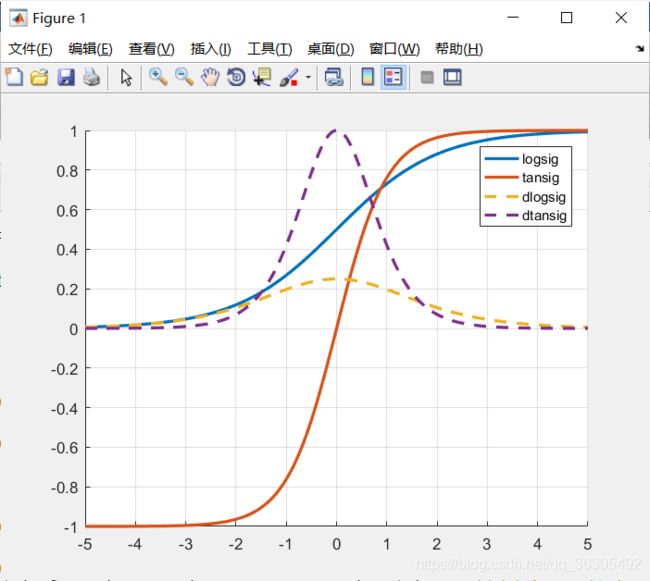
输入和权值都是正常的数。不做解释，常见的f(x)有以下几个。

前三个函数都很好理解，我说一下s型函数(图上两条实线，我的取值范围是-5:5,)

显然s函数输入为(-∞,+∞),输出为（0,1）；

双极S函数输入为(-∞,+∞),输出为（-1,1）；他们一般作为BP神经网络的隐含层激活函数。那什么是BP神经网络呢

这里这篇博文解释的很好https://blog.csdn.net/lyxleft/article/details/82840787我也不在赘述了，BP网络的英文（Error Back propagation）及误差反向传播，所以BP网络的核心在于误差的梯度

多说无益，直接上代码。原理这种东西还是要数学好才能看懂

二、手写代码

1.主代码

clear all;
clc;
%%读取原始数据
%原始数据格式如下表所示
%          | QF1（变量1）|QF2（变量2）|QF3（变量2）|err（输出结果）|
%  样本1   |    1	       |      0	    |     0	     |     1         |
%  样本2   |    0	       |      1	    |     0	     |     2         |

data_trian=xlsread('电网故障数据.xlsx');
data_test=xlsread('电网故障数据.xlsx',2);

traind=data_trian(1:315,1:60);%读取训练数据矩阵格式 样本数*变量数
trainl=data_trian(1:315,61);%读取训练数据目标结果矩阵格式 样本数*变量数

testd=data_test(1:70,1:60);%读取测试数据矩阵格式 样本数*变量数
testl=data_test(1:70,61)';%读取测试数据目标结果矩阵格式 样本数*变量数
%% 配置BP神经网络参数
numberOfSample = 315; %输入样本数量
numberOfTestSample = 70;%测试样本数量


numberOfHiddenNeure = 8;%自己的神经网络的隐含层的个数
inputDimension = 60;%自己的神经网络的输入变量的个数
outputDimension = 1;%学习输出层数目（即有几个目标输出）

%由系统时钟种子产生随机数
rng(0);
%对训练集中的输入数据矩阵和目标数据矩阵进行归一化处理
 traind_s=nomalp(traind);%对训练数据归一化
 sampleInput = traind_s'; %归一化数据转置改为 变量数*样本的形式便于和权值相乘
 
 output=(nomalp(trainl))';%归一化训练目标（输出）数据矩阵

%噪声强度
noiseIntensity = 0.01;
%利用正态分布产生噪声
noise = noiseIntensity * randn(outputDimension, numberOfSample);
%给样本输出矩阵tmp添加噪声，防止网络过度拟合
sampleOutput = output+ noise ;%

%最大训练次数
maxEpochs = 50000;

%网络的学习速率
learningRate = 0.0001;
%训练网络所要达到的目标误差
error0 = 0.65*10^(-3);
%初始化输入层与隐含层之间的权值
W1 = 0.5 * rand(numberOfHiddenNeure, inputDimension) - 0.1;
%初始化输入层与隐含层之间的阈值
B1 = 0.5 * rand(numberOfHiddenNeure, 1) - 0.1;
%初始化输出层与隐含层之间的权值
W2 = 0.5 * rand(outputDimension, numberOfHiddenNeure) - 0.1;
%初始化输出层与隐含层之间的阈值
B2 = 0.5 * rand(outputDimension, 1) - 0.1;

%保存能量函数(误差平方和)的历史记录
errorHistory = zeros(1,maxEpochs);
%% 学习函数
for i = 1:maxEpochs
    %隐含层输出
    hiddenInput=W1 * sampleInput + repmat(B1, 1, numberOfSample);
    hiddenOutput = logsig(hiddenInput);
    %输出层输出
    networkOutput = W2 * hiddenOutput + repmat(B2, 1, numberOfSample);
    %实际输出与网络输出之差
    error = sampleOutput - networkOutput;
    %计算能量函数(误差平方和)
    E = sumsqr(error);
    errorHistory(i) = E;

    if E < error0
        break;
    end

    %以下依据能量函数的负梯度下降原理对权值和阈值进行调整
    delta2 = error;
    delta1 = W2' * delta2.*dlogsig(hiddenInput,hiddenOutput);

    dW2 = delta2 * hiddenOutput';
    dB2 = delta2 * ones(numberOfSample, 1);

    dW1 = delta1 * sampleInput';
    dB1 = delta1 * ones(numberOfSample, 1);

    W2 = W2 + learningRate * dW2;
    B2 = B2 + learningRate * dB2;

    W1 = W1 + learningRate * dW1;
    B1 = B1 + learningRate * dB1;
end

%% 下面对已经训练好的网络进行(仿真)测试

testSampleInput = nomalp(testd)';%归一化测试目标（输入）数据矩阵
 testl_n=nomalp(testl');%归一化测试目标（输出）数据矩阵
%对测试样本进行处理

testHiddenOutput = logsig(W1 * testSampleInput + repmat(B1, 1, numberOfTestSample));
testNetworkOutput =  W2 * testHiddenOutput + repmat(B2, 1, numberOfTestSample);

%还原网络输出层的结果(反归一化)

out_out2=enomalp(testNetworkOutput',testl');
out_out3=out_out2;
%因为结果是整数我们根据经验将输出转化为整数
for i=1:numberOfTestSample
    out_out2(i)=fix(out_out2(i));
    temp=out_out3(i)-out_out2(i);
    if(temp>=0.5)
        out_out2(i)=out_out2(i)+1;
    end
end
%% 测试结果输出
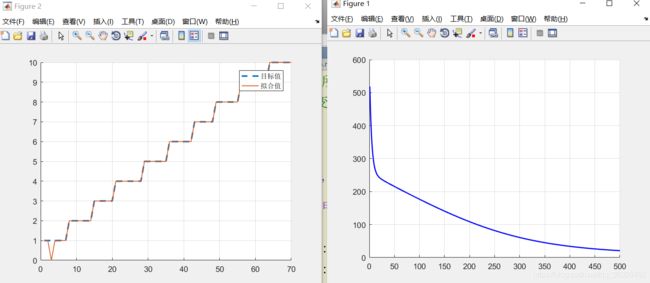
rate=sum(out_out2'==testl)/length(testl);
fprintf('正确率:\n   %f%%\n',rate*100);

figure(1)
axis on
hold on
grid
[nRow,nCol]=size(errorHistory);
plot(1:500,errorHistory(1:500),'b-','LineWidth',1.5);
hold off

figure(2)
hold on
grid
plot(1:numberOfTestSample, testl,'--','LineWidth', 2); 	% 绘制真实目标曲线
plot(1:numberOfTestSample, out_out2, 'LineWidth', 1); % 绘制拟合结果
legend('目标值', '拟合值'); hold off              	% 加图标
hold off

 

输出结果

 

这里我说几个我调试代码的心得：

1，学习率很关键，学习率的取值是关系你能不能学习成功的一个很重要的因素之一，学习率的选择一定要看你的输入数据和权值误差乘积之后会不会过大，如果过大可能会造成无法收敛。

2，隐含层的选的影响到你学习的正确率，隐含层选取的三个原则。（我是的操作方法是先根据输入单元数带入3式子，得到一个n的大概范围，再计算2式，根据这两个式子得到的n一个个带入一式，看看你的样本数是多少，本例子中

最后求出n为7,8时样本量和实际样本量契合，经过模拟最终发现隐含层为8的正确率更高）

2.归一化函数

什么是归一化？

——将数据映射到[0, 1]或[-1, 1]区间或其他的区间。

为什么要归一化？

–  输入数据的单位不一样，有些数据的范围可能特别大，导致的结果是神经网络收敛慢、训练时间长。

–  数据范围大的输入在模式分类中的作用可能会偏大，而数据范围小的输入作用就可能会偏小。(防止数据湮灭等现象)

–  由于神经网络输出层的激活函数的值域是有限制的，因此需要将网络训练的目标数据映射到激活函数的值域。例如神经网络的输出层若采用S形激活 函数，由于S形函数的值域限制在(0,1)，也就是说神经网络的输出只能限制在(0,1)，所以训练数据的输出就要归一化到[0,1]区间。

–  S形激活函数在(0,1)区间以外区域很平缓，区分度太小。例如S形函数f(X)在参数a=1时，f(100)与f(5)只相差0.0067。这样数据的差异就会失去意义！

二、Z-score标准化方法

    这种方法给予原始数据的均值（mean）和标准差（standard deviation）进行数据的标准化。经过处理的数据符合标准正态分布，即均值为0，标准差为1，转化函数为：

其中为所有样本数据的均值，为所有样本数据的标准差。

function output=nomalp(input)

[~,w]=size(input);
mm=mean(input);%每行求平均值
ml=[1:w];
for i=1:w
    output(:,i)=input(:,i)-mm(1,i); 
end

for i=1:w
    ml(i)=std(output(:,i));
end

for i=1:w
    if ml(i)==0;
    else   
         output(:,i)=output(:,i)/ml(i);
    end
end

end

2.反归一化函数

我们按照原思路知道原数据的情况下将数据还原即可

function output=enomalp(nomalp,ongnizep)

[~,w]=size(ongnizep);
mm=mean(ongnizep);%每行求平均值
ml=[1:w];
for i=1:w
    output(:,i)=ongnizep(:,i)-mm(1,i); 
end

for i=1:w
    ml(i)=std(output(:,i));
end

for i=1:w
    if ml(i)==0;
    else   
         output(:,i)=output(:,i)/ml(i);
    end
end

for i=1:w
    if ml(i)==0;
    else   
         output(:,i)=nomalp(:,i)*ml(i)+mm(1,i);
    end
end

end

 

二、工具箱代码

 如果调试不出来可以先用工具箱函数，测试输入数据的正确性

clear all
clc;
rng('default');
rng(0);
data_trian=xlsread('电网故障数据.xlsx');
data_test=xlsread('电网故障数据.xlsx',2);
traind=data_trian(1:315,1:60);
trainl=data_trian(1:315,61);
testd=data_test(1:70,1:60);
testl=data_test(1:70,61)';
%对训练集中的输入数据矩阵和目标数据矩阵进行归一化处理
 traind_n=nomalp(traind)';% 输入矩阵（变量数 x 样本数）
 output=(nomalp(trainl))';% 目标矩阵（目标数 x 样本数）
 testd_n=nomalp(testd)';
 testl_n=nomalp(trainl);
									
									

%% 2、训练网络

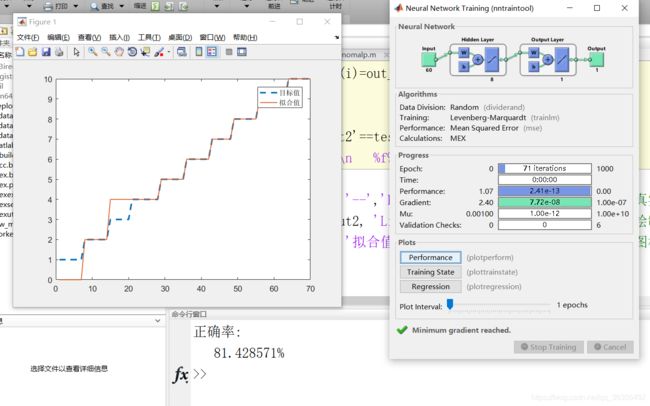
net = newff(traind_n,output, 8);  					% 定义网络结构，一个隐含层，含50个神经元
net = train(net,traind_n,output);  					% 训练网络
outputs = net(testd_n);            					% 训练结果
out_out2=enomalp(outputs',testl');
out_out3=out_out2;

for i=1:70
    out_out2(i)=fix(out_out2(i));
    temp=out_out3(i)-out_out2(i);
    if(temp>=0.5)
        out_out2(i)=out_out2(i)+1;
    end
end
 rate=sum(out_out2'==testl)/length(testl);
fprintf('正确率:\n   %f%%\n',rate*100);
%% 3、可视化  
plot(1:70, testl,'--','LineWidth', 2); hold on   	% 绘制真实目标曲线
plot(1:70, out_out2, 'LineWidth', 1);               	% 绘制拟合结果
legend('目标值', '拟合值'); hold off              	% 加图标
 

 

输出结果如下

可以看到不加控制工具箱函数学习正确率就比较低了。

---

总结

BP神经网络作为最基础的人工学习之一，在学习方面容易陷入局部最优化解，后期我会继续学习RBF和PNN神经网络并系统分析他们的优缺点。