Image Super-Resolution via Iterative Refinement 论文解读和感想
随着20年DDPM的提出,近两年提出了大量基于Denoising Diffusion的图像处理模型,本文便是谷歌在21年 CVPR提出的基于Denoising Diffusion的图像超分模型。
背景动机
Image SR已经是低级视觉任务中元老级别的任务了,存在大量的基于不同的生成范式的Image SR模型,但是作者开局便对几种基于常见的生成范式的模型不足点进行了概括:
首先是自回归模型,虽然其模型间接,想法直观,但是对于高分辨率图像,其计算量实在太大。然后是正态流模型(Normalizing Flows)和VAE模型,由于重采样的存在,以及过分依赖重构,在低级视觉任务中通过只能产生次优解,表现在可视化上就是过于平滑,缺乏texture信息。GAN虽然能克服以上问题,但是玩过GAN的都知道,GAN的训练太难了,一不小心就崩溃了。此时,Denoising Diffusion模型的优势就体现出来了:既不需要精心设计优化过程防止崩溃,又能生成富含texture的结果。并且由于Denoising Diffusion模型是级联模型,因此可以将整个优化过程拆开进行,这对于显卡资源紧张的小伙伴们非常友好。
方法介绍
首先对Denoising Diffusion模型的基本概念介绍一下(由于这个生成范式比较新,因此近几年基于这个范式的文章都会对其进行简要介绍)。对于一组数据 D = { x i , y i } i = 1 N D = \{x_i, y_i\}^N_{i=1} D={xi,yi}i=1N,其中 x i x_i xi是低分图, y i y_i yi是对应的高分图,那么本文的条件DDPM模型的目标就是从一个与 y y y分辨率相同的高斯噪声图 y T y_T yT出发,不断的去噪获得最终的目标高分图 y 0 y_0 y0,其中每一步都可以以马尔科夫链的方式表示成一个条件概率分布 f θ ( y t − 1 ∣ y t , x ) f_{\theta}(y_{t-1}|y_t,x) fθ(yt−1∣yt,x)的形式。
前向过程
首先来讲解前向扩散过程。对于目标高分图 y 0 y_0 y0,我们通过 T T T次添加高斯噪声,使得其逐渐转化为一个高斯噪声,其过程可以表示为:
q ( y 1 : T ∣ y 0 ) = Π t = 1 T q ( y t ∣ y t − 1 ) q(y_{1:T}|y_0) = \Pi^T_{t=1}q(y_t|y_{t-1}) q(y1:T∣y0)=Πt=1Tq(yt∣yt−1)
q ( y t ∣ y t − 1 ) = N ( y t ∣ α t y t − 1 , ( 1 − α t ) I ) q(y_t|y_{t-1}) = N(y_t|\sqrt\alpha_t y_{t-1},(1-\alpha_t)I) q(yt∣yt−1)=N(yt∣αtyt−1,(1−αt)I)
其中 α t \sqrt \alpha_t αt可以看成是在第t步添加的噪声的强度,这个强度是一个超参数,并且有个规律是开始时大,越往后越小,当然这个规律是沿用了DDPM。并且通过推导可知,由于每一步添加的都是标准高斯噪声,因此第t步的高分噪声图 y t y_t yt的分布我们可以直接通过
q ( y t ∣ y 0 ) = N ( y t ∣ γ ) q(y_t|y_0) = N(y_t|\sqrt \gamma) q(yt∣y0)=N(yt∣γ)
来获得,其中 γ t = Π i = 1 t α i \gamma_t = \Pi^t_{i=1} \alpha_i γt=Πi=1tαi。那么其后验概率就是
q ( y t − 1 ∣ y 0 , y t ) = N ( y t − 1 ∣ μ , σ 2 I ) q(y_{t-1}|y_0,y_t) = N(y_{t-1}|\mu,\sigma^2I) q(yt−1∣y0,yt)=N(yt−1∣μ,σ2I),其中
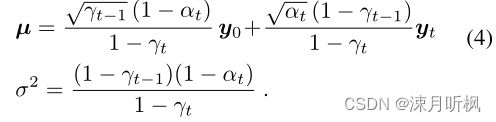
模型优化目标
由上面的分析可知,对于任意时刻的噪声高分图,我们可以通过:
y ~ = γ y 0 + 1 − γ ϵ \tilde{y} = \sqrt \gamma y_0 + \sqrt{1-\gamma} \epsilon y~=γy0+1−γϵ (5)
来显式的表示,其中 ϵ ∼ N ( 0 , I ) \epsilon \sim N(0,I) ϵ∼N(0,I),通过调整 γ \gamma γ可以达到目的。也就是说,当我们获得任意一个阶段的高分噪声图,由于 γ \gamma γ是已知的,只需要显式的获得 ϵ \epsilon ϵ就可以得到 y 0 y_0 y0。所以本文将优化目标定义为:
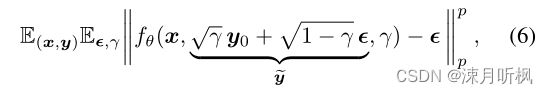
这里要说一下,这个优化目标作者应该也是直接参照了DDPM中的优化目标:
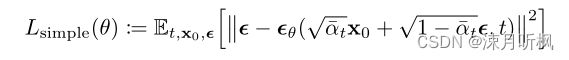
在DDPM中作者通过一系列的分析给出,这种形式的优化目标相比于直接对 y 0 y_0 y0进行回归,对变分下界更加友好并且更加容易实现,当然本文在对比实验部分同样给出了直接对 y 0 y_0 y0进行回归的版本,并进行了性能比较。
推断过程
DDPM的推断过程模拟的是逆向马尔科夫链,对于给定的高斯噪声 y T y_T yT,有
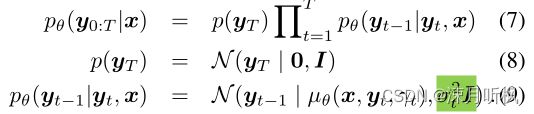
(9)式给出了在已知 y t y_t yt的情况下,获得 y t − 1 y_{t-1} yt−1的方法,可以看到,由于方差是已知的,那么要想重采样 y t − 1 y_{t-1} yt−1实际上就是用网络来拟合其均值 μ θ \mu_\theta μθ。回看(5)式,由于 f θ f_\theta fθ经过训练后可以近似拟合 ϵ \epsilon ϵ,那么也就是说对于任意 y t y_t yt我们可以通过下式近似得到 y 0 y_0 y0:
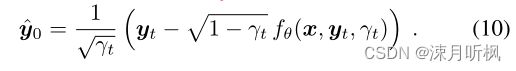
看上去到这里似乎就达到我们的目标了,但是本文并不是到此结束了。回顾(4)式,作者将得到的 y ^ 0 \hat{y}_0 y^0带入到了(4)式中,得到了均值:
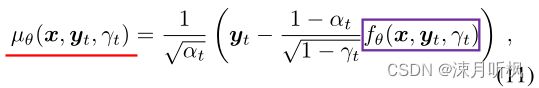
然后通过分布来对 y t − 1 y_{t-1} yt−1进行采样:
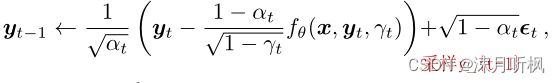
然后再将 y t − 1 y_{t-1} yt−1带入到 f θ f_\theta fθ中,重复上述过程,直到采样无噪声的 y 0 y_0 y0。虽然作者说这个方法是follow的DDPM,然而我个人的理解是这样可以通过多次采样引入更多的随机性,从而达到类似于GAN的生成多样性。
实验结果分析
最后再来说一下实验部分
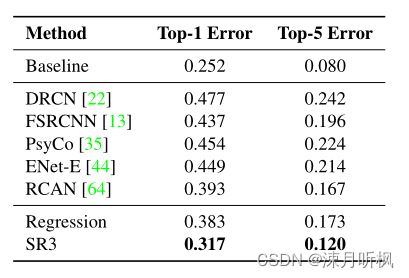
首先作者借用前人工作,指出尽管当前图像任务常用PSNR和SSIM来衡量结果性能,然而这两个指标却反对模型对结果的创新,所以在这两项指标上,对 ϵ \epsilon ϵ进行估计的方式要差于直接对 y 0 y_0 y0进行回归的训练方式。
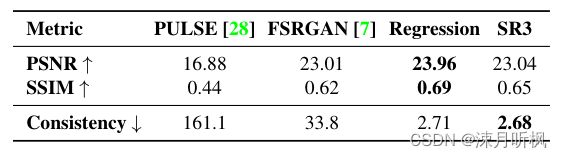
然而作者指出,对于FID这种对整体特征相似度进行评估的质量指标,对 ϵ \epsilon ϵ进行估计的方式要明显更好,并且一致性(生成的高分图的下采样和低分图的相似度)要更好。这充分说明对 ϵ \epsilon ϵ进行估计的方式在保证生成结果的真实性的前提下,有着更好的多样性,反应在可视化上就是有着更加丰富的纹理。
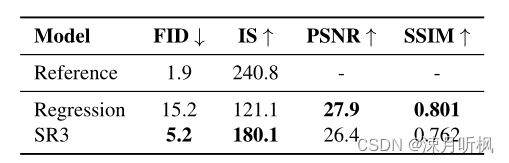
此外,对 ϵ \epsilon ϵ进行估计的方式在下游任务上效果也是更好,以下是生成高分图的分类精度比较: