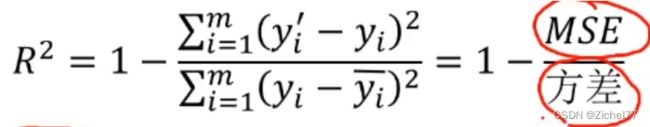Python3人工智能学习笔记（一）——线性回归
文章目录
- 1. 线性回归
-
- 1.1 概念
- 1.2 回归问题求解
- 1.3 求解a和b
- 2. 线性回归实战准备
-
- 2.1 Scikit-Learn
- 2.2 调用Sklearn求解线性回归问题
- 2.3 评估模型表现
-
- 2.3.1 均方误差MSE
- 2.3.2 R 2 R^2 R2值
- 2.3.3 编程
- 2.4 图形展示
-
- 1.画散点图
- 2.多张图同时展示
- 3. 多因子线性回归实战
-
- 流程
1. 线性回归
回归分析：根据数据，确定两种或两种以上变量之间互相依赖的定量关系
1.1 概念
回归分析中，变量与因变量存在线性关系
y=ax+b
属于监督学习的范畴
1.2 回归问题求解
1.确定P、A定量关系
P=f(A)，大概去拟合
线性模型：
y=ax+b
重点是找到合适的a和b
y’是预测值
希望y’和y二者距离和最小化
公式进一步转换为
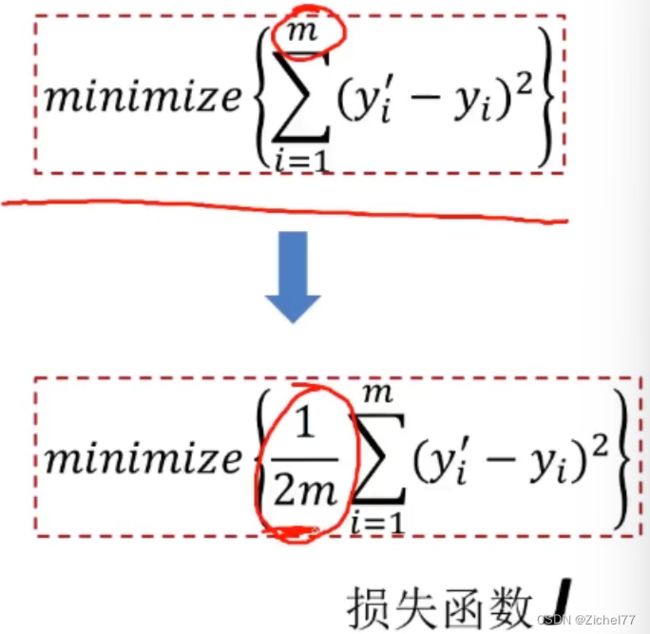再÷一个2m，m是样本的数量，是为了方便求解，后需要求导，可以把m约掉，不影响整体结果。因为m是常数，所以和上面的公式求解结果是一样的。变成希望损失函数J尽可能小
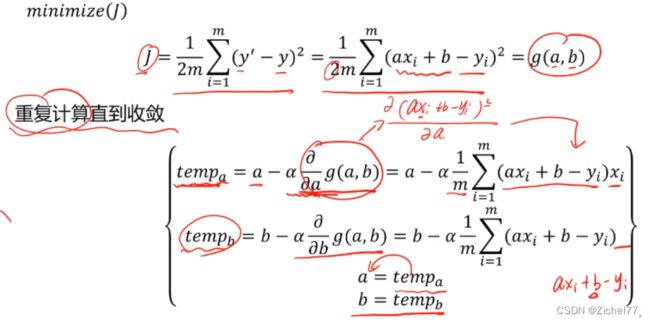
1.3 求解a和b
使用的是梯度下降法，将y’用a和b带入，就变成了g(a,b)，然后对a,b分别进行梯度下降法求解
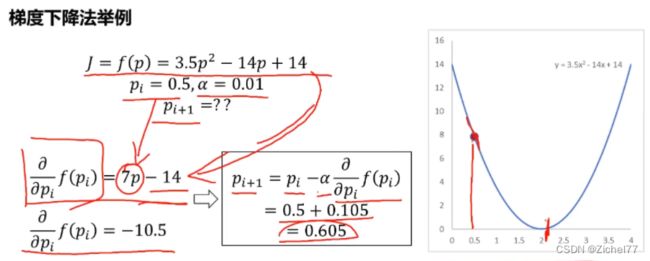之后无论是逻辑回归的分类还是神经网络模型的核心原理都是如此（梯度下降）
编程实现如下
就是tempa为临时变量，然后阿尔法是步长，乘上求一次偏导，平方移到前面和1/2m的2约掉了，所以变成1/m
每一次运算结束后对a进行更新，直至收敛
2. 线性回归实战准备
2.1 Scikit-Learn
解决机器学习问题的开源框架
包括数据预处理、分类、回归、降维、模型选择
2.2 调用Sklearn求解线性回归问题
- 寻找a、b（y=ax+b）
`from sklearn.linear_model import LinearRegression`
调用LinearRegression这样一个工具包
`Ir_model=LinearRegression()`
通过库创建实际的对象
`Ir_model.fit(x,y)`
通过model.fit即可找出x,y即a,b
- 展示a,b
`a=Ir_model.coef`
`b=Ir_model.intercept_`
- 对新数据做预测
`predictions=Ir_model.predict(x_new)`
2.3 评估模型表现
2.3.1 均方误差MSE
和损失函数只相差一个1/2
越小越好（接近0）
2.3.2 R 2 R^2 R2值
更好地了解拟合得好不好
越接近1越好
2.3.3 编程
计算y与y’的MSE和R2_score
`from sklearn.metrics import mean_squared_error,r2_score`
调用包
`MSE=mean_squared_error(y,y+predict)`
实际的y和预测的y作为变量输入
`R2=r2_score(y,y_predict)`
还可以画图对比y和y’，可视化模型表示
`from matplotlib import pyplot as plt`
`plt.scatter(y,y’)`
- y’ vc y集中度越高越好（越接近直线分布）
2.4 图形展示
1.画散点图
`import matplotlib.pyplot as plt`
`plt.scatter(x,y)`
2.多张图同时展示
`fig1=plt.subplot(211)`
211就是分成2行1列，填入到第1行中
`plt.scatter(x1,y1)`
`fig2=plt.subplot(212)`
212就是分成2行1列，填入到第2行中
`plt.scatter(x2,y2)`
3. 多因子线性回归实战
也是先从单因子出发
流程
基于usa_housing_price.csv数据，建立线性回归模型，预测合理房价
- 以面积为输入变量，建立单因子模型，评估模型表现，可视化线性回归预测结果
- 以income、house age、numbers of rooms、population、area作为输入变量，建立多因子模型，评估模型表现
- 预测Income=65000，House of Rooms=5，Population=30000，Size=200的合理房价