遗传算法和非线性规划问题
遗传算法的适应性改造
遗传算法如何运用到非线性规划中?其重点在于染色体DNA排列模式和浮点数、负数的转化关系。如果使用 Python 实现遗传算法,则非常适用于正数的整数规划,因为生成 0-1 随机数非常简单,这样就可以使用二进制换算生成各种正数。
因此,如果需要使用遗传算法解决非线性规划(非线性规划完全可以用粒子群算法替代,但是多思考一定是好的),就需要将生成的二进制数转化为十进制之后再通过标准化换算入区间中。结合其他约束条件,就可以对个体进行自然选择。
import numpy as np
from tqdm import tqdm
class GeneticAlgorithm(object):
def __init__(self, func, geneSize, geneNum, groupSize, crossRate, mutationRate):
self.func = func # 适应值评估函数
self.geneSize = geneSize # 单个基因的长度
self.geneNum = geneNum # 基因数量
self.groupSize = groupSize # 种群数量
self.crossRate = crossRate # 交叉互换概率
self.mutationRate = mutationRate # 变异概率
self.POP = np.random.randint(0, 2, (groupSize, geneSize * geneNum)) # 直接初始化种群
self.Bounds = np.array([[-np.inf, np.inf]] * geneNum) # 初始化边界
self.operationTimes = 0 # 初始化迭代次数
self.bestValue = -np.inf # 记录全局最优值
self.bestAnswer = np.zeros(geneNum) # 记录全局最优解
# 设置自变量区间,传入值为列表形式
def setBounds(self, Bounds):
self.Bounds = np.array(Bounds)
# 设置迭代次数,传入值为整数
def setOperationTimes(self, operationTimes):
self.operationTimes = operationTimes
def CalculateFitness(self): # 转化为十进制并计算适应度值
transPOP = np.zeros((self.groupSize, self.geneNum)) # 转化后的种群,初始化
for i in range(self.geneNum): # 一个一个基因进行计算
vi = self.POP[:, self.geneSize * i : self.geneSize * (i + 1)]
transPOP[:, i] = vi.dot(2 ** np.arange(self.geneSize))
transPOP[:, i] = (transPOP[:, i] / 2 ** self.geneSize) * (self.Bounds[i][1] - self.Bounds[i][0]) + self.Bounds[i][0]
# 强行塞进区间,让本算法中的二进制换算模式"也可以表示浮点数并且突破正号的限制"
# 计算适应度
value = np.apply_along_axis(self.func, 1, transPOP)
return transPOP, value # 返回转化后的种群值和个体适应度
def Selection(self):
transPOP, value = self.CalculateFitness() # 得到转化值和适应度值
cumsumvalue = (value/value.sum()).cumsum()
# 记录全局最优值
if value.max() > self.bestValue:
self.bestValue = value.max()
self.bestAnswer = transPOP[value.argmax()]
# 轮盘赌算法进行自然选择,并扩充种群规模
newPOP = []
while len(newPOP) < self.groupSize:
tmp = np.random.uniform()
newPOP.append(self.POP[cumsumvalue >= tmp][0])
# 得到新种群后重置原种群
self.POP = np.array(newPOP)
def CrossAndMutation(self): # 交叉互换和随机变异一起完成
for i in range(self.groupSize):
child = self.POP[i]
if np.random.uniform() < self.crossRate:
mother = np.random.randint(0, self.groupSize)
position = np.random.randint(0, self.geneNum * self.geneSize)
child = np.concatenate([child[:position], self.POP[mother][position:]])
# 随机发生变异
if np.random.uniform() < self.mutationRate:
position = np.random.randint(0, self.geneNum * self.geneSize)
# 更改该位置的基因
child[position] = 1 - child[position]
self.POP[i] = child
def Calculation(self):
print("遗传算法 开始计算(近似)最优化解")
# 最后一次迭代是不需要发生变异的,因此只循环 operatoinTimes-1 次
for i in tqdm(range(self.operationTimes - 1)):
self.Selection()
self.CrossAndMutation()
# 最后一次自然选择
self.Selection()
print("遗传算法 计算完毕 现在输出最优解")
print(f"全局最优值是: {self.bestValue}")
print(f"全局最优解为: {self.bestAnswer}")
这里对传统遗传算法思路进行了一定的修改:
- 在 CalculateFitness() 函数中,将二进制数转化为十进制后用 min-max-scale 方法标准化进入自变量区间,这样就不用担心在种群演变过程中出现有个体的自变量超出范围的情况;
- 因为图方便,没有添加其他的约束条件。约束条件将会使用函数传入的方式补入类中,后续工作就是添加这一功能,完善库函数;
- 在传统遗传算法的基础上添加了记录全局最优解的功能,这一点思路取自全局粒子群算法。这样可以省去在一系列选择后得到的种群中挑选最优值的工作,因为最优值和最优解可以通过直接调用变量获取。
我们使用修改后的遗传算法求解一个简单问题:
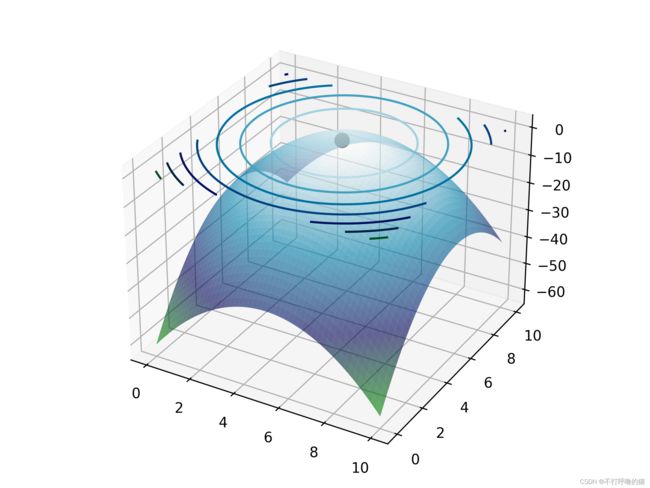
m i n f ( x 1 , x 2 ) = ( x 1 − 5 ) 2 + ( x 2 − 6 ) 2 , 0 ≤ x 1 , x 2 ≤ 10 minf(x_1, x_2)=(x_1-5)^2+(x_2-6)^2,0\leq x_1,x_2\leq10 minf(x1,x2)=(x1−5)2+(x2−6)2,0≤x1,x2≤10
只需要在功能区中初始化类对象并调用优化函数即可,非常的简便。
def func(x): # 变量的传入形式为数组
return -(x[0] - 5) ** 2 - (x[1] - 6) ** 2
if __name__ == "__main__":
project = GeneticAlgorithm(
func = func,
geneNum = 2, # 基因数量为 2
geneSize = 6, # 基因用 6 位二进制数表示
groupSize = 50, # 种群数量为 50
crossRate = .9, # 交叉互换的概率为 0.9
mutationRate = .1 # 随机变异的概率为 0.1
)
# 设置自变量范围
project.setBounds([[0, 10], [0, 10]])
# 设置迭代次数为 5000 次
project.setOperationTimes(5000)
project.Calculation()
最后,可以得到如下图所示的近似结果。如果增加迭代次数(比如增加到 10000 次以上),可以得到更加精确的点。