动手强化学习（八）：DQN 改进算法——Dueling DQN

文章转于 伯禹学习平台-动手学强化学习 （强推）
本文所有代码均可在jupyter notebook运行
与君共勉，一起学习。

1. 简介

  DQN 算法敲开了深度强化学习的大门，但是作为先驱性的工作，其本身存在着一些问题以及一些可以改进的地方。于是，在 DQN 之后，学术界涌现出了非常多的改进算法。本章将介绍其中两个非常著名的算法：Double DQN 和 Dueling DQN，这两个算法的实现非常简单，只需要在 DQN 的基础上稍加修改，它们能在一定程度上改善 DQN 的效果。

2. Dueling DQN

Dueling DQN 是 DQN 另一种的改进算法，它在传统 DQN 的基础上只进行了微小的改动，但却能大幅提升 DQN 的表现。在强化学习中，我们将状态动作价值函数 $Q$ 减去状态价值函数 $V$ 的结果定 义为优势函数 $A$ ，即 $A(s,a)=Q(s,a)-V(s)$ 。在同一个状态下，所有动作的优势值之和为 0 ，因为所有动作的动作价值的期望就是这个状态的状态价值。据此，在 Dueling DQN 中，Q网络被 建模为：
$$Q_{\eta ,\alpha ,\beta }(s,a)=V_{\eta ,\alpha }(s)+A_{\eta ,\beta }(s,a)$$
其中， $V_{\eta ,\alpha }(s)$ 为状态价值函数，而 $A_{\eta ,\beta }(s,a)$ 则为该状态下采取不同动作的优势函数，表示采取不同动作的差异性； $\eta$ 是状态价值函数和优势函数共享的网络参数，一般用在神经网络中，用来提 取特征的前几层; 而 $\alpha$ 和 $\beta$ 分别为状态价值函数和优势函数的参数。在这样的模型下，我们不再让神经网络直接输出 $Q$ 值，而是训练神经网络的最后几层的两个分支，分别输出状态价值函数和优势 函数，再求和得到 $Q$ 值。Dueling DQN 的网络结构如图所示。

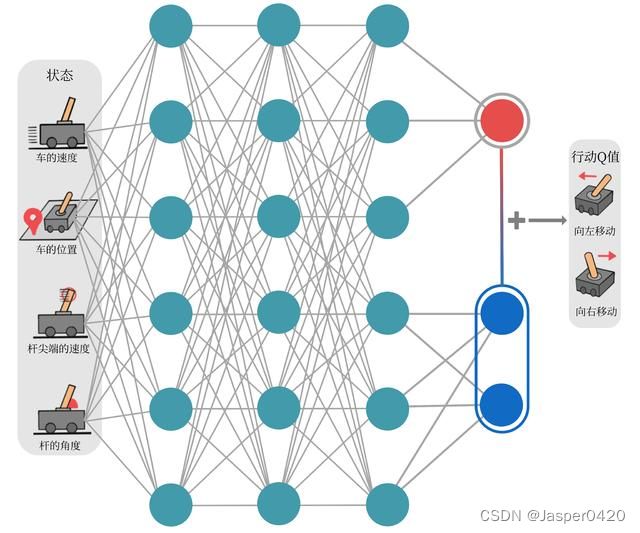
将状态价值函数和优势函数分别建模的好处在于：某些情境下智能体只会关注状态的价值，而并不关心不同动作导致的差异，此时将二者分开建模能够使智能体更好地处理与动作关联较小的状态。在下图所示的驾驶车辆游戏中，智能体注意力集中的部位被显示为橙色，当智能体前面没有车时，车辆自身动作并没有太大差异，此时智能体更关注状态价值，而当智能体前面有车时（智能体需要超车），智能体开始关注不同动作优势值的差异。

对于 Dueling DQN 中的公式 $Q_{\eta ,\alpha ,\beta }(s,a)=V_{\eta ,\alpha }(s)+A_{\eta ,\beta }(s,a)$ ，它存在对于 $V$ 值和 $A$ 值建模不唯一性的问题。例如，对于同样的 $Q$ 值，如果将 $V$ 值加上任意大小的常数 $C$ ，再将所有 $A$ 值减去 $C$ ，则得到的 $Q$ 值依然不变，这就导致了训练的不稳定性。为了解决这一问题，Dueling DQN 强制最优动作的优势函数的实际输出为 0 ，即:
$$Q_{\eta ,\alpha ,\beta }(s,a)=V_{\eta ,\alpha }(s)+A_{\eta ,\beta }(s,a)-\underset{a^{\prime }}{\max }{A}_{\eta ,\beta }\left(s,a^{\prime }\right)$$
此时 $V(s)={\max }_{a}Q(s,a)$ ，可以确保 $V$ 值建模的唯一性。在实现过程中，我们还可以用平均代替最大化操作，即：
$$Q_{\eta ,\alpha ,\beta }(s,a)=V_{\eta ,\alpha }(s)+A_{\eta ,\beta }(s,a)-\frac{1}{|\mathcal{A}|}\sum _{a^{\prime }}{A}_{\eta ,\beta }\left(s,a^{\prime }\right)$$
此时 $V(s)=\frac{1}{|\mathcal{A}|}{\sum }_{a^{\prime }}Q\left(s,a^{\prime }\right)$ 。在下面的代码实现中，我们将采取此种方式，虽然它不再满足贝尔曼最优方程，但实际应用时更加稳定。

有人可能会问：“为什么 Dueling DQN 会比 DQN 好? "部分原因在于 Dueling DQN 能更高效学习状态价值函数。每一次更新时，函数 $V$ 都会被更新，这也会影响到其他动作的 $Q$ 值。而传统的 DQN 只会更新某个动作的 $Q$ 值，其他动作的 $Q$ 值就不会更新。因此，Dueling DQN 能够更加频繁、准确地学习状态价值函数。

3. Dueling DQN 代码实践

Dueling DQN 与 DQN 相比的差异只是在网络结构上，大部分代码依然可以继续沿用。我们定义状态价值函数和优势函数的复合神经网络VAnet。

class VAnet(torch.nn.Module):
    ''' 只有一层隐藏层的A网络和V网络 '''
    def __init__(self, state_dim, hidden_dim, action_dim):
        super(VAnet, self).__init__()
        self.fc1 = torch.nn.Linear(state_dim, hidden_dim)  # 共享网络部分
        self.fc_A = torch.nn.Linear(hidden_dim, action_dim)
        self.fc_V = torch.nn.Linear(hidden_dim, 1)

    def forward(self, x):
        A = self.fc_A(F.relu(self.fc1(x)))
        V = self.fc_V(F.relu(self.fc1(x)))
        Q = V + A - A.mean(1).view(-1, 1)  # Q值由V值和A值计算得到
        return Q


class DQN:
    ''' DQN算法,包括Double DQN和Dueling DQN '''
    def __init__(self,
                 state_dim,
                 hidden_dim,
                 action_dim,
                 learning_rate,
                 gamma,
                 epsilon,
                 target_update,
                 device,
                 dqn_type='VanillaDQN'):
        self.action_dim = action_dim
        if dqn_type == 'DuelingDQN':  # Dueling DQN采取不一样的网络框架
            self.q_net = VAnet(state_dim, hidden_dim,
                               self.action_dim).to(device)
            self.target_q_net = VAnet(state_dim, hidden_dim,
                                      self.action_dim).to(device)
        else:
            self.q_net = Qnet(state_dim, hidden_dim,
                              self.action_dim).to(device)
            self.target_q_net = Qnet(state_dim, hidden_dim,
                                     self.action_dim).to(device)
        self.optimizer = torch.optim.Adam(self.q_net.parameters(),
                                          lr=learning_rate)
        self.gamma = gamma
        self.epsilon = epsilon
        self.target_update = target_update
        self.count = 0
        self.dqn_type = dqn_type
        self.device = device

    def take_action(self, state):
        if np.random.random() < self.epsilon:
            action = np.random.randint(self.action_dim)
        else:
            state = torch.tensor([state], dtype=torch.float).to(self.device)
            action = self.q_net(state).argmax().item()
        return action

    def max_q_value(self, state):
        state = torch.tensor([state], dtype=torch.float).to(self.device)
        return self.q_net(state).max().item()

    def update(self, transition_dict):
        states = torch.tensor(transition_dict['states'],
                              dtype=torch.float).to(self.device)
        actions = torch.tensor(transition_dict['actions']).view(-1, 1).to(
            self.device)
        rewards = torch.tensor(transition_dict['rewards'],
                               dtype=torch.float).view(-1, 1).to(self.device)
        next_states = torch.tensor(transition_dict['next_states'],
                                   dtype=torch.float).to(self.device)
        dones = torch.tensor(transition_dict['dones'],
                             dtype=torch.float).view(-1, 1).to(self.device)

        q_values = self.q_net(states).gather(1, actions)
        if self.dqn_type == 'DoubleDQN':
            max_action = self.q_net(next_states).max(1)[1].view(-1, 1)
            max_next_q_values = self.target_q_net(next_states).gather(
                1, max_action)
        else:
            max_next_q_values = self.target_q_net(next_states).max(1)[0].view(
                -1, 1)
        q_targets = rewards + self.gamma * max_next_q_values * (1 - dones)
        dqn_loss = torch.mean(F.mse_loss(q_values, q_targets))
        self.optimizer.zero_grad()
        dqn_loss.backward()
        self.optimizer.step()

        if self.count % self.target_update == 0:
            self.target_q_net.load_state_dict(self.q_net.state_dict())
        self.count += 1


random.seed(0)
np.random.seed(0)
env.seed(0)
torch.manual_seed(0)
replay_buffer = rl_utils.ReplayBuffer(buffer_size)
agent = DQN(state_dim, hidden_dim, action_dim, lr, gamma, epsilon,
            target_update, device, 'DuelingDQN')
return_list, max_q_value_list = train_DQN(agent, env, num_episodes,
                                          replay_buffer, minimal_size,
                                          batch_size)

episodes_list = list(range(len(return_list)))
mv_return = rl_utils.moving_average(return_list, 5)
plt.plot(episodes_list, mv_return)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('Dueling DQN on {}'.format(env_name))
plt.show()

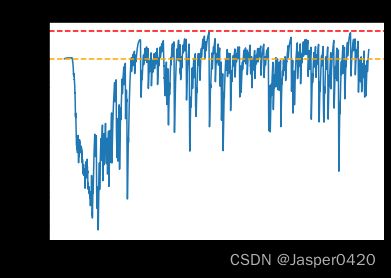
frames_list = list(range(len(max_q_value_list)))
plt.plot(frames_list, max_q_value_list)
plt.axhline(0, c='orange', ls='--')
plt.axhline(10, c='red', ls='--')
plt.xlabel('Frames')
plt.ylabel('Q value')
plt.title('Dueling DQN on {}'.format(env_name))
plt.show()
-------------------------------------------------------------------------------------------
Iteration 0: 100%|████████████████████████████████████████| 20/20 [00:10<00:00,  1.87it/s, episode=20, return=-708.652]
Iteration 1: 100%|████████████████████████████████████████| 20/20 [00:15<00:00,  1.28it/s, episode=40, return=-229.557]
Iteration 2: 100%|████████████████████████████████████████| 20/20 [00:15<00:00,  1.32it/s, episode=60, return=-184.607]
Iteration 3: 100%|████████████████████████████████████████| 20/20 [00:13<00:00,  1.50it/s, episode=80, return=-200.323]
Iteration 4: 100%|███████████████████████████████████████| 20/20 [00:13<00:00,  1.51it/s, episode=100, return=-213.811]
Iteration 5: 100%|███████████████████████████████████████| 20/20 [00:13<00:00,  1.53it/s, episode=120, return=-181.165]
Iteration 6: 100%|███████████████████████████████████████| 20/20 [00:14<00:00,  1.35it/s, episode=140, return=-222.040]
Iteration 7: 100%|███████████████████████████████████████| 20/20 [00:14<00:00,  1.35it/s, episode=160, return=-173.313]
Iteration 8: 100%|███████████████████████████████████████| 20/20 [00:12<00:00,  1.62it/s, episode=180, return=-236.372]
Iteration 9: 100%|███████████████████████████████████████| 20/20 [00:12<00:00,  1.57it/s, episode=200, return=-230.058]

根据代码运行结果我们可以发现，相比于传统的 DQN，Dueling DQN 在多个动作选择下的学习更加稳定，得到的回报最大值也更大。由 Dueling DQN 的原理可知，随着动作空间的增大，Dueling DQN 相比于 DQN 的优势更为明显。之前我们在环境中设置的离散动作数为 11，我们可以增加离散动作数（例如 15、25 等），继续进行对比实验。

4. 对 Q 值过高估计的定量分析

对 $\mathrm{Q}$ 值过高估计的定量分析 $Q_{\omega }-(s,a)-V^{\ast }$ 服从 $[-1,1]$ 之间的均匀独立同分布；假设动作空间大小为 $m_{\circ }$ 。那么，对于任意状态 $s$ ，有:
$$\mathbb{E}\left[\underset{a}{\max }{Q}_{{\omega }^{-}}(s,a)-\underset{a^{\prime }}{\max }{Q}_{\ast }\left(s,a^{\prime }\right)\right]=\frac{m-1}{m+1}$$
即状态空间 $m$ 越大时， $Q$ 值过高，估计越严重。
证明: 将估算误差记为 ${ϵ}_a=Q_{{\omega }^{-}}(s,a)-{\max }_{a^{\prime }}{Q}^{\ast }\left(s,a^{\prime }\right)$ ，由于估算误差对于不同的动作是独立的，因此有:
$$P\left(\underset{a}{\max }{ϵ}_a\le x\right)=\prod _{a=1}^{m}P\left({ϵ}_a\le x\right)$$
$P\left({ϵ}_a\le x\right)$ 是 ${ϵ}_a$ 的累积分布函数 (cumulative distribution function，即 CDF)，它可以具体被写为:
$$P\left({ϵ}_a\le x\right)=\{\begin{array}{ll}0& \text{ if }x\le -1\\ \frac{1+x}{2}& \text{ if }x\in (-1,1)\\ 1& \text{ if }x\ge 1\end{array}$$
因此，我们得到关于 ${\max }_a{ϵ}_a$ 的累积分布函数:
$$\begin{array}{rl}P\left(\underset{a}{\max }{ϵ}_a\le x\right)& =\prod _{a=1}^{m}P\left({ϵ}_a\le x\right)\\ & =\{\begin{array}{ll}0& \text{ if }x\le -1\\ {\left(\frac{1+x}{2}\right)}^m& \text{ if }x\in (-1,1)\\ 1& \text{ if }x\ge 1\end{array}\end{array}$$
最后我们可以得到:
$$\begin{array}{rl}\mathbb{E}\left[\underset{a}{\max }{ϵ}_a\right]& ={\int }_{-1}^{1}x\frac{\mathrm{d}}{\mathrm{d}x}P\left(\underset{a}{\max }{ϵ}_a\le x\right)\mathrm{d}x\\ & ={\left[{\left(\frac{x+1}{2}\right)}^m\frac{mx-1}{m+1}\right]}_{-1}^1\\ & =\frac{m-1}{m+1}\end{array}$$
虽然这一分析简化了实际环境，但它仍然正确刻画了$\mathrm{Q}$ 值过高估计的一些性质，比如$\mathrm{Q}$ 值的过高估计随动作空间大小$m$ 的增加而增加，换言之，在动作选择数更多的环境中，$\mathrm{Q}$ 值的过高估计会更严重。

总结

在传统的 DQN 基础上，有两种非常容易实现的变式——Double DQN 和 Dueling DQN，Double DQN 解决了 DQN 中对$Q$值的过高估计，而 Dueling DQN 能够很好地学习到不同动作的差异性，在动作空间较大的环境下非常有效。从 Double DQN 和 Dueling DQN 的方法原理中，我们也能感受到深度强化学习的研究是在关注深度学习和强化学习有效结合：一是在深度学习的模块的基础上，强化学习方法如何更加有效地工作，并避免深度模型学习行为带来的一些问题，例如使用 Double DQN 解决$Q$值过高估计的问题；二是在强化学习的场景下，深度学习模型如何有效学习到有用的模式，例如设计 Dueling DQN 网络架构来高效地学习状态价值函数以及动作优势函数。

相关资源来自：伯禹学习平台-动手学强化学习