Notes: One-shot Adversarial Attacks on Visual Tracking with Dual Attention

One-shot Adversarial Attacks on Visual Tracking with Dual Attention

Paper can be found here.

Important features:

• free-model ( black-box?)
• only add perturbations in the initial frame

Introduction

Challenges to address:

1. First, online visual tracking is unable to pre-know the category of tracked and to learn beforehand because of the free-model tacked target and the continuous video frames.
2. Secondly, it is difficult to set an optimization objective to generate adversarial examples since a successful attack on the tracking task is significantly different from that on the multi-classification task which could merely maximize the probability of the class with the second-highest confidence. Specifically, the tracking task in each frame is the same as that of classifying all candidate boxes into one positive sample and the others into negative samples. Such a special binary classification problem makes it difficult to perform a successful attack if only one candidate box is selected to increase its confidence. (not quite understood)
3. Last but not least, different from the NMS (Non-Maximum Suppression) algorithm used in the detection, the Gaussian windows are widely applied to refine the box confidences in the tracking task, which induces difficulties to balance the strength and the success of the attack.

This paper target trackers based on Siamese networks, proposes a one-shot attack framework— only slightly perturbing the pixel values of the object patch in the initial frame of a video, which achieves the goal of attacking the tracker in subsequent frames, i.e. failure to the tracking of SiamRPN.

Methodology

To address the challenges:

1. To attack arbitrary targets, this method only add perturbations to the first frame of each video, namely one-shot attack.
2. The attack must be able to perturb certain number of candidates. This paper optimizes two losses: a batch confidence loss to reduce confidence of high-quality boxes and raise confidence of low-quality boxes, and a feature loss for general attack.
3. To improve attack power, this paper employs dual attention mechanism.
   – batch confidence loss: confidence attention.
   – feature loss: feature attention.

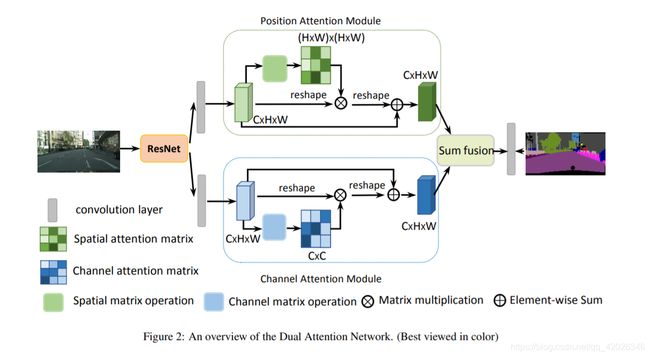
Dual-attention network
reference: https://arxiv.org/abs/1809.02983

“Attention is, to some extent, motivated by how we pay visual attention to different regions of an image or correlate words in one sentence.
"In a nutshell, attention in deep learning can be broadly interpreted as a vector of importance weights: in order to predict or infer one element, such as a pixel in an image or a word in a sentence, we estimate using the attention vector how strongly it is correlated with (or “attends to” as you may have read in many papers) other elements and take the sum of their values weighted by the attention vector as the approximation of the target."reference

One-shot attack with dual loss

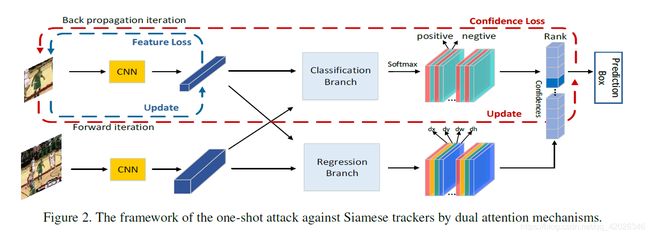
Given: initial frame; ground truth bbox of the tracked target.
Goal: generate an adversarial target image $z^{\ast }=z+\Delta z.$

$$z^{\ast }=\underset{|z_k-z_k^{\ast }|\le \epsilon }{\mathrm{argmin}}\mathcal{L}(z,z^{\ast })$$

$z$: target patch
$z_k$: the per pixel of clean image of image $z$
$z_k^{\ast }$: the per pixel of clean image of the adversary.

Batch confidence loss
The purpose of this approach based on batch confidence is to suppress the candidates with high confidence and stimulate the can didates with moderate confidence.
$${\mathcal{L}}_1=\sum _{{\mathcal{R}}_{1:p}}f(z^{\ast },x_i)-\sum _{{\mathcal{R}}_{q:r}}f(z^{\ast },x_i),s.t.|z_k-z_k^{\ast }|\le \epsilon$$

$X$: search area around the target and twice the size of it, including $n$ candidates $\{x_1,x_2,...,x_n\}$.
$f(z,x_i)$: tracking model which takes $z$ and $x_i$ as inputs and the confidence of each candidate as the output.
${\mathcal{R}}_{1:n}$: ranking of the confidence of $n$ candidates.
${\mathcal{R}}_{1:p}$: the sort in the first $p$.
${\mathcal{R}}_{q:r}$: the sort from $q$ to $r$.

Feature loss
The Euclidean distance of the feature maps of $z$ and $z^{\ast }$ are maximized.
$${\mathcal{L}}_2=-\sum _{j=1:C}||{\varphi }_j(z^{\ast })-{\varphi }_j(z)|{|}_2,s.t.|z_k-z_k^{\ast }|\le \epsilon$$

$\varphi (\cdot )$: feature map of CNNs.
$C$: channels

Dual attention attack

Confidence attention
By applying the confidence attention mechanism to the loss function, we can distinguish the degree of suppression and stimulation for the candidates with different confidences.
The confidence loss function is rewritten as:
$${\mathcal{L}}_1^{\ast }=\sum _{{\mathcal{R}}_{1:p}}\{w_i\ast f(z^{\ast },x_i)\}-\sum _{{\mathcal{R}}_{q:r}}f(z^{\ast },x_i),s.t.|z_k-z_k^{\ast }|\le \epsilon$$
$$w_i=\frac{1}{a+b\cdot \tanh (c\cdot (d(x_i)-d(x_1)))}$$
$d(x_i)$: the coordinates distance between the any $i$-th candidate $x_i$ and first $x_1$ in the sorted confidence list.

Feature attention
This paper further considers the channel-wise activation-guided attention of feature maps to distinguish the importance of different channels, which will guarantee the generalization ability of the one-shot attack.
The confidence loss function is rewritten as:
$${\mathcal{L}}_2^{\ast }=-\sum _{j=1:C}||w_j^{\prime }\cdot {\varphi }_j(z^{\ast })-{\varphi }_j(z)|{|}_2,s.t.|z_k-z_k^{\ast }|\le \epsilon$$

$$w_j=\frac{1}{a^{\prime }+b^{\prime }\cdot \tanh (c^{\prime }\cdot (m({\varphi }_j(z))-m({\varphi }_j(z){)}_{min}))}$$

$m(\cdot )$: the mean of each channel
${\varphi }_j(z)$
$m(\cdot {)}_{min}$: the minimum mean

Dual attention loss
$$\mathcal{L}=\alpha {\mathcal{L}}_1^{\ast }+\beta {\mathcal{L}}_2^{\ast }$$

In the implementation, we use Adam optimizer to minimize the loss by iteratively perturbing the pixels along the gradient directions within the patch area, and the generation process stops when the number of iterations reaches 100 or the first candidate of the ranking ${\mathcal{R}}_{\tau }[1]$ behinds $p$ in the initial ranking ${\mathcal{R}}_0$.

Adam: a method for efficient stochastic optimization that only requires first-order gradients with little memory requirement. The method computes individual adaptive learning rates for different parameters from estimates of first and second moments of the gradients; the name Adam is derived from adaptive moment estimation.