2019 Deep point-to-subspace metric learning for sketch-based 3D shape retrieval学习笔记
文章目录
- 摘要
- 目前的主要挑战
- 本文的主要贡献
- 模型框架
-
- 特征抽取
- 代表性视图选择网络
- 深度点到子空间的度量学习
本期论文
@article{Lei2019DeepPM,
title={Deep point-to-subspace metric learning for sketch-based 3D shape retrieval},
author={Yinjie Lei and Ziqin Zhou and Pingping Zhang and Yulan Guo and Zijun Ma and Lingqiao Liu},
journal={Pattern Recognit.},
year={2019},
volume={96}
}
原文链接
摘要
目前大多数跨模态检索问题都是将草图和三维形状投影到一个公共空间中,该空间可以通过相似度/距离,计算跨模态相似度。然而,给一个查询草图,只有三维形状的部分视点是有代表性的。因此在不考虑查询草图而盲目的将三维形状投影到一个特征空间将不可避免地带来查询草图没有代表性的信息。本文提出的方法为深度点到子空间的度量学习框架——将草图表示成一个特征向量而将三维模型映射到一个由几个选定的基特征向量表示的子空间。他们之间的相似性被定义为一个查询特征向量到其在子空间中最近点的距离。值得注意的是,最近点是查询自适应的并且可以映射出给予草图所对应的有代表性的视点信息。
然而为了有效的构建一个这样的深度网络,我们用一个特殊设计的分类器将它当成分类问题去解决它。为了减少三维形状的冗余度,本文也设计了一个代表性视图选择网络。
目前的主要挑战
1.手绘草图是一个主观性的活动,每个人画出来的草图都有较大的差异。
2.草图和三维模型有着较大的跨模态差异
3.草图只能反应出三维形状的某些视图,三维形状的不同视图差异又会比较明显。
由于草图只能代表3D形状的部分视图,而非代表性的视图贡献又很小甚至具有负作用,然而现存的模型是在不考虑视点信息的情况下平等的对待每个视图。所以本文提出了深度点到子空间的度量学习的框架。首先,一个代表性视图的选择网络获取了三维形状的几个代表性视图,然后从所选的视图中生成一个由特征向量张成的子空间,随后动态求解一个优化问题,将草图与三维形状之间的相似性定义为草图特征向量与其在子空间中最近的点之间的距离,值得注意的一点是:最近的点是自适应查询的,是由查询草图所获得的视点信息
本文的主要贡献
1.设计了一个代表性视图选择网络来确定三维模型最具有代表性的视图,来减少三维模型的冗余性。
2.DPSML框架被提出来计算查询自适应相似度用来草图搜模型。
3.将代表性学习问题被看作为一个分类问题来使得训练过程更加高效。
4.在三个公共数据集SHREC’13,SHREC’14和SHREC’16进行了完整的实验和比较,来展示所提出模型的更好的表现。
模型框架
本文的模型由两个分支组成,由预先训练的深度模型 f F M f_{F}^{M} fFM和 f F S f_{F}^{S} fFS来分别学习草图和三维模型的原始特征,他们在不共享权重的情况下有着相同的结构,然后RVS(代表性视图选择网络)被用来获得三维形状渲染视图的融合权值,并生成代表性视图。接下来,两个度量网络 f M M f_{M}^{M} fMM和 f M S f_{M}^{S} fMS都被用来减少被抽取特征的维度。因此一个草图被特征向量描述为表示空间中的“点”,而三维形状由代表视图中的特征向量表示为“子空间”。我们为每个类随机初始化一个“虚拟中心”,并开发一个带有修正损失函数的DPSML框架,注意,从“点”到“子空间”的距离是通过动态求解一个优化问题来计算的。
框架的实现步骤如下:
1.首先三维形状被投影为12张视角下二维图片,提取草图和三维模型的提前训练好的模型有AlexNet,VGG和ResNet,被用来抽取草图和三维形状的原始特征。结果,草图有一个特征向量和三维模型有12个特征向量。
2.然后一个代表性视图选择模块被用来选择最具有代表性视图。
3.随后动态求解一个优化问题,将草图与三维形状之间的相似性定义为草图特征向量与其在子空间中最近的点之间的距离,值得注意的一点是:最近的点是自适应查询的,是由查询草图所获得的视点信息。
特征抽取
被提出的框架通过在训练过程中解决了一个分类问题来学习草图和三维模型的表示, 分类器层是共享的,以确保两种模态下的表示在每个类中都是相似的和接近的。草图的特征被表示为 V F S V_{F}^{S} VFS,三维形状被表示为 V F M V_{F}^{M} VFM。
代表性视图选择网络
获得n个初始特征向量之后,然而有些视角下的特征向量是冗余的,他们在代表性上有相似性如下图所示:
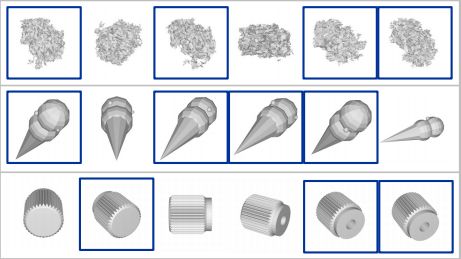
所以为了减少模型的复杂度, f R f_{R} fR被引入来得到 n ∗ n^* n∗个特征向量,用于增强表示。 n ∗ n^* n∗表示被选择有代表性视图是远少于n的。
工作框架如下图所示
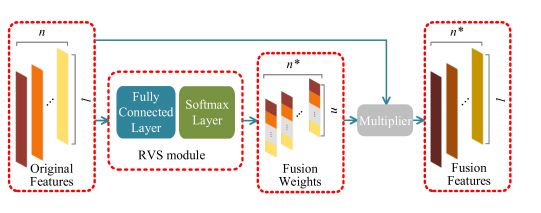
RVS模块是由一个全连接层跟着一个softmax层组成的,在原始的基于视图的特征向量上执行了n*次加权和池化操作,对于每个操作,求和池的权重由一个专门的注意函数计算。特征从RVS模块输出以后,与原始特征做一次乘积操作,生成最终的融合特征。
深度点到子空间的度量学习
在执行检索的时候,我们需要计算草图和三维模型的距离来对检索结果进行排序,因为草图被描述为一个点而三维模型被描述为一个子空间,所以 V M S V_{M}^{S} VMS和 V M M V_{M}^{M} VMM之间的距离可以被表述为点到子空间上最近点的距离。如下图所示:
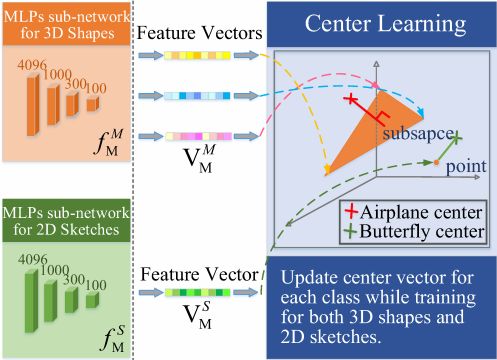
所得公式如下:

每个草图被描述为一个特征向量 V M S V_{M}^{S} VMS,草图和所有类中心的距离 d S d^{S} dS可以被计算为
d S d^{S} dS = [ d 1 S d_{1}^{S} d1S, d 2 S d_{2}^{S} d2S,…, d k S d_{k}^{S} dkS],with
d t S = ∣ ∣ V S − c t ∣ ∣ 2 d_{t}^{S} = ||V^{S} - c_{t}||_{2} dtS=∣∣VS−ct∣∣2
