聚类算法-dbscan的简易代码实现
最近的组会经常会听到这个名词,所以趁着今天有空,所以准备了解下这个算法。
先从百度 百科开始切入:
DBSCAN(Density-Based Spatial Clustering of Applications with Noise)是一个比较有代表性的基于密度的聚类算法。与划分和层次聚类方法不同,它将簇定义为密度相连的点的最大集合,能够把具有足够高密度的区域划分为簇,并可在噪声的空间数据库中发现任意形状的聚类。
上面的解释中有【簇】的概念,先攻破它!
簇:将物理或抽象对象的集合分成由类似的对象组成的多个类的过程被称为聚类。由聚类所生成的簇是一组数据对象的集合,这些对象与同一个簇中的对象彼此相似,与其他簇中的对象相异。
【题外话】现在理解,认为簇就是一些样本的集合比如说{[1,2,3],[0,2,3],[2,3,4]}。
descan是一种基于密度的聚类方法,下面我们研究下具体操作。
形式化定义
DBSCAN中的几个定义:
Ε邻域:将某 对象半径为Ε内的区域称为该对象的Ε邻域;
核心对象:如果给定对象Ε邻域内的样本点数大于等于MinPts,则称该对象为核心对象;
【题外话】MinPts这是一个参数,这个参数的用途以后看懂了再说。看到了,MInPts 是最小包含点数(minPts)
直接密度可达:对于样本集合D,如果样本点q在p的Ε邻域内,并且p为核心对象,那么对象q从对象p直接密度可达。
密度可达:对于样本集合D,给定一串样本点p1,p2….pn,p= p1,q= pn,假如对象pi从pi-1直接密度可达,那么对象q从对象p密度可达。
密度相连:存在样本集合D中的一点o,
如果对象o到对象p和对象q都是密度可达的,那么p和q密度相联。
可以发现,密度可达是直接密度可达的传递闭包,并且这种关系是非对称的。密度相连是对称关系。DBSCAN目的是找到密度相连对象的最大集合。
Eg: 假设半径Ε=3,MinPts=3,点p的E邻域中有点{m,p,p1,p2,o}, 点m的E邻域中有点{m,q,p,m1,m2},点q的E邻域中有点{q,m},点o的E邻域中有点{o,p,s},点s的E邻域中有点{o,s,s1}.
那么核心对象有p,m,o,s(q不是核心对象,因为它对应的E邻域中点数量等于2,小于MinPts=3);
点m从点p直接密度可达,因为m在p的E邻域内,并且p为核心对象;
点q从点p密度可达,因为点q从点m直接密度可达,并且点m从点p直接密度可达;
点q到点s密度相连,因为点q从点p密度可达,并且s从点p密度可达
算法的执行步骤
DBScan需要二个参数: 扫描半径 (eps)和最小包含点数(minPts)。 任选一个未被访问的点开始,找出与其距离在eps之内(包括eps)的所有附近点。
- 如果 附近点的数量 ≥ minPts,则当前点与其附近点形成一个簇,并且出发点被标记为已访问(visited)。 然后递归,以相同的方法处理该簇内所有未访问的点,从而对簇进行扩展。
- 如果 附近点的数量 < minPts,则该点暂时被标记作为噪声点。
- 如果簇充分地被扩展,即簇内的所有点被标记为已访问,然后用同样的算法去处理未被访问的点。
下面分析下怎么写代码
先定义数据类型,首先数据的类型为:[x,y],其中,x,y分别i表示两个坐标。
然后,为了方便计算,我们将其拓展为以下数据结构:

Visited表示是否被访问,Cluster表示所属于的簇。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
df=pd.read_csv("./data/三坨散点.csv")
# 调整一下数据集,由于原来的数据集是两个条目,下面我们要新增两个条目,一个是访问,一个是聚类
df["visited"]=np.zeros(df.shape[0])# 使用这种方法可以在dataframe中新增加一列,同理的
df["cluster"]=np.zeros(df.shape[0])# 使用这种方法可以在dataframe中新增加一列,同理的,并将其都初始化为0
D=np.array(df) # 现在就将数据集设置好了
接下来,涉及到一个很重要的东西,就是距离的计算,我们要计算样本间的欧氏距离,从而得到某点是否在有效半径中。
def Euclid_distance(x,y):
#中学,学过的两点间距离公式
length=x.shape[0]
sum=0
for i in range(length):
sum=sum+(x[i]-y[i])*(x[i]-y[i])
return np.sqrt(sum)# 开平方
有了距离函数,差不多可以根据百度百科的伪代码,进行主函数的编写了。
def DBSCAN(D,Eps,MinPts):
# (数据集,半径,最小数)
C=-1# 初始化 簇的编号
while len(D)!= 0:# 判断一下样本中是否还有未访问的节点。
print(len(D))# 输出下剩余节点数
for p in D :# 下面开始遍历下每一个节点
if p[VISITED]==1:# 其实没必要了,因为已经过滤过一遍了
continue# 如果是已经访问的节点,那麽跳过本次循环
p[VISITED]=1 #将i标记为已访问
N = getNeighbours (D,p, Eps);
if len(N) < MinPts :#如果满足len(N) < MinPts,则将p标记为噪声
p[CLUSTER] = -1
else:
C+=1 #建立新簇C
ExpandCluster(p,N, C, Eps, MinPts,0)# 拓展这个节点的其他同类
D=getUnvisited(D)# 将D更新未没有访问的节点
以上就是我们的主函数了,但是会发现有几个函数并没有实例化出来,下面我们就逐个击破。从getNeighbours(D,p,Eps)开始。这个函数的目的是,发现中心点p周围Eps 半径内的所有的点。并把这些点组成一个集合。
 我们可以先进行一个矩形的筛选:
我们可以先进行一个矩形的筛选:
如果不在矩形之内,直接淘汰,不用计算距离。
如果在矩形内,先计算距离,然后判断是否在Eps中,这样可以减少计算量。
def getNeighbours(D,p,Eps):
neighbours_set=[]
# 先划分一个方形区域,作为候选集,然后在进行欧氏距离的计算,这样效率会更高
min_x,min_y,max_x,max_y=p[0]-Eps,p[1]-Eps,p[0]+Eps,p[1]+Eps
# 可是这样比较,计算复杂度也不低啊,或许会好一点吧
D=getUnvisited(D)# 只在乎没有被访问的点。
for j in D:
if j[0]<min_x or j[0]>max_x or j[1]<min_y or j[1]>max_y :
continue
# 由于有四个数据,我们只需要前两个
if Euclid_distance(p[:-2], j[:-2]) < Eps :
# 如果小于Eps 将其加入到这个子集中
neighbours_set.append(j)
return neighbours_set
并且,我还要过滤下已经访问过的节点。
def getUnvisited(D):
data=[]
for i in D:
if i[VISITED]==0:# 表示没有访问过
data.append(i)
return data
def ExpandCluster(p, N, C, Eps, MinPts,deep):
if deep>=80:#防止 超过最大栈循环。
return
#(当前节点,候选集,聚类,半径,最小数)
p[CLUSTER]=C # 将节点p设置为这个簇,因为这个是验证过的
for p_ex in N:
p_ex[VISITED] = 1# 将节点标记为已经访问
N_ex= getNeighbours(D,p_ex, Eps);# 获得相关节点的边缘节点
if p_ex[CLUSTER] ==0:
p_ex[CLUSTER]=C # 将p_ex 加入簇C
ExpandCluster(p_ex,N_ex,C,Eps,MinPts,deep+1)#增加一次栈深
下面使用matplotlib 包进行画图
def show_data(D):
cluster_numb=int(max(D[:,CLUSTER]))+2
# 将噪声值也作为一类 假设最大簇编号为2 ,那么有 -1,0,1,2 共四个簇。也就是2+2 ,所以上文用最大值+2
print(cluster_numb)
# 也就是说,现在有cluster_numb类数据,我们要划分为cluster_numb个数据
cluster_x=[[] for i in range(cluster_numb)]
cluster_y=[[] for i in range(cluster_numb)]
for i in D:
#由于这个簇编号是从-1 开始的,而索引是从0开始,所以要+1
cluster_x[int(i[CLUSTER])+1].append(i[0])
cluster_y[int(i[CLUSTER])+1].append(i[1])
colors=['red','brown','orange','green','cyan','purple','pink','blue','#FFA07A','#20B2AA','#87CEFA','#9ACD32']
for index in range(cluster_numb):#读取每一个簇的点的信息,并用不同颜色标识。
plt.scatter(cluster_x[index],cluster_y[index],alpha=0.5,c=colors[index])#画一个散点图
plt.show()
至此,关键函数,已经编写结束。下面给出源代码,和测试数据。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
df=pd.read_csv("./data/三坨散点.csv")
# 下面应该定义一个计算距离的函数
def Euclid_distance(x,y):
length=x.shape[0]
sum=0
for i in range(length):
sum=sum+(x[i]-y[i])*(x[i]-y[i])
return np.sqrt(sum)
#返回一个欧氏距离
# 下面做些正事,选择一个点,判断他是不是核心对象,首先要把数据分组,
# 现在我们接触的都是二维数据,所以比较好处理,把df 变成一个列表
# 设置数据集为[x,y,VISITED,CLUSTER]
def ExpandCluster(p, N, C, Eps, MinPts,deep):
if deep>=80:#防止 超过最大栈循环。
return
#(当前节点,候选集,聚类,半径,最小数)
p[CLUSTER]=C # 将节点p设置为这个簇,因为这个是验证过的
for p_ex in N:
p_ex[VISITED] = 1# 将节点标记为已经访问
N_ex= getNeighbours(D,p_ex, Eps);# 获得相关节点的边缘节点
if p_ex[CLUSTER] ==0:
p_ex[CLUSTER]=C # 将p_ex 加入簇C
ExpandCluster(p_ex,N_ex,C,Eps,MinPts,deep+1)#增加一次栈深
def getNeighbours(D,p,Eps):
neighbours_set=[]
# 先划分一个方形区域,作为候选集,然后在进行欧氏距离的计算,这样效率会更高
min_x,min_y,max_x,max_y=p[0]-Eps,p[1]-Eps,p[0]+Eps,p[1]+Eps
# 可是这样比较,计算复杂度也不低啊,或许会好一点吧
D=getUnvisited(D)# 只在乎没有被访问的点。
for j in D:
if j[0]<min_x or j[0]>max_x or j[1]<min_y or j[1]>max_y :
continue
# 由于有四个数据,我们只需要前两个
if Euclid_distance(p[:-2], j[:-2]) < Eps :
# 如果小于Eps 将其加入到这个子集中
neighbours_set.append(j)
return neighbours_set
def getUnvisited(D):
data=[]
for i in D:
if i[VISITED]==0:
data.append(i)
return data
def show_data(D):
cluster_numb=int(max(D[:,CLUSTER]))+2
# 将噪声值也作为一类 假设最大簇编号为2 ,那么有 -1,0,1,2 共四个簇。也就是2+2 ,所以上文用最大值+2
print(cluster_numb)
# 也就是说,现在有cluster_numb类数据,我们要划分为cluster_numb个数据
cluster_x=[[] for i in range(cluster_numb)]
cluster_y=[[] for i in range(cluster_numb)]
for i in D:
#由于这个簇编号是从-1 开始的,而索引是从0开始,所以要+1
cluster_x[int(i[CLUSTER])+1].append(i[0])
cluster_y[int(i[CLUSTER])+1].append(i[1])
colors=['red','brown','orange','green','cyan','purple','pink','blue','#FFA07A','#20B2AA','#87CEFA','#9ACD32']
for index in range(cluster_numb):#读取每一个簇的点的信息,并用不同颜色标识。
plt.scatter(cluster_x[index],cluster_y[index],alpha=0.5,c=colors[index])#画一个散点图
plt.show()
def DBSCAN(D,Eps,MinPts):
# (数据集,半径,最小数)
C=-1# 初始化 簇的编号
while len(D)!= 0:# 判断一下样本中是否还有未访问的节点。
print(len(D))# 输出下剩余节点数
for p in D :# 下面开始遍历下每一个节点
if p[VISITED]==1:# 其实没必要了,因为已经过滤过一遍了
continue# 如果是已经访问的节点,那麽跳过本次循环
p[VISITED]=1 #将i标记为已访问
N = getNeighbours (D,p, Eps);
if len(N) < MinPts :#如果满足len(N) < MinPts,则将p标记为噪声
p[CLUSTER] = -1
else:
C+=1 #建立新簇C
ExpandCluster(p,N, C, Eps, MinPts,0)# 拓展这个节点的其他同类
D=getUnvisited(D)# 将D更新未没有访问的节点
VISITED=2
CLUSTER=3
MinPts=8 #领域密度阀值,表示在这个区域内包含的样本数.
Eps=0.35#半径参数
# 调整一下数据集,由于原来的数据集是两个条目,下面我们要新增两个条目,一个是访问,一个是聚类
df["visited"]=np.zeros(df.shape[0])# 使用这种方法可以在dataframe中新增加一列,同理的
df["cluster"]=np.zeros(df.shape[0])# 使用这种方法可以在dataframe中新增加一列,同理的,并将其都初始化为0
D=np.array(df) # 现在就将数据集设置好了
DBSCAN(D,Eps,MinPts)
show_data(D)
【注这个数据集在这个文件同目录的data目录下】,下载后需要放到相同位置。数据集
 测试结果:
测试结果:

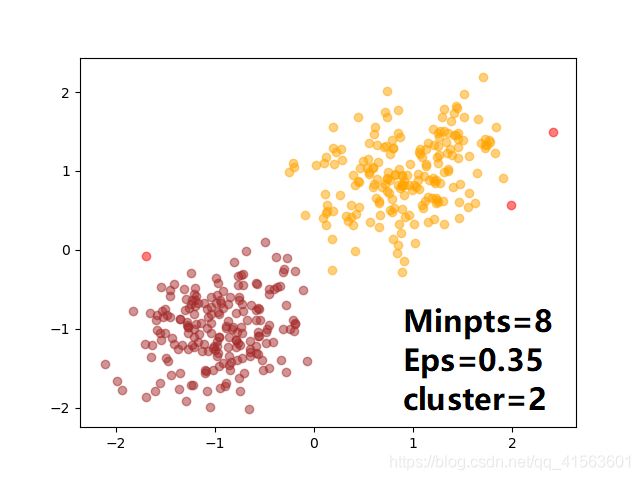

对于5个簇的表现效果不佳。
实验进行了(2020/11/06)一天时间,并不是十分完善,欢迎交流