深度学习优化算法：梯度下降GD、随机梯度下降SGD、小批量梯度下降MBGD、动量法(momentum)

原文链接：动手学深度学习pytorch版：优化算法7.1-7.4
github：https://github.com/ShusenTang/Dive-into-DL-PyTorch

最好去看一下原书和GitHub，讲解更加详细。

虽然梯度下降在深度学习中很少被直接使用，但理解梯度的意义以及沿着梯度反方向更新自变量可能降低目标函数值的原因是学习后续优化算法的基础。

1. 梯度下降

1.1 一维梯度下降

我们先以简单的一维梯度下降为例, 解释梯度下降算法可能降低目标函数值的原因。假设连续可导的函数 $f:\mathbb{R}\to \mathbb{R}$ 的输入和输出都是标量。给 定绝对值足够小的数 $ϵ$, 根据泰勒展开公式，我们得到以下的近似:
$$f(x+ϵ)\approx f(x)+ϵf^{\prime }(x)$$

这里 $f^{\prime }(x)$ 是函数 $f$ 在 $x$ 处的梯度。一维函数的梯度是一个标量，也称导数。

这意味着，如果通过
$$x\leftarrow x-\eta f^{\prime }(x)$$

来迭代 $x$, 函数 $f(x)$ 的值可能会降低。因此在梯度下降中, 我们先选取一个初始值 $x$ 和常数 $\eta >0$, 然后不断通过上式来迭代 $x$, 直到达到停止条 件, 例如 $f^{\prime }(x{)}^2$ 的值已足够小或迭代次数已达到某个值。

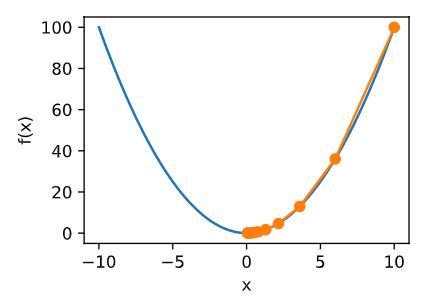
下面我们以目标函数 $f(x)=x^2$ 为例来看一看梯度下降是如何工作的。虽然我们知道最小化 $f(x)$ 的解为 $x=0$, 这里依然使用这个简单函数来观 察 $x$ 是如何被迭代的。首先，导入本节实验所需的包或模块。

%matplotlib inline
import numpy as np
import torch
import math
import sys
sys.path.append("..") 
import d2lzh_pytorch as d2l
import os
os.environ["KMP_DUPLICATE_LIB_OK"]="TRUE"

接下来使用 $x=10$ 作为初始值，并设 $\eta =0.2$。 使用梯度下降对 $x$ 迭代10次，可见最终 $x$ 的值较接近最优解。

def gd(eta):
    x = 10
    results = [x]
    for i in range(10):
        x -= eta * 2 * x  # f(x) = x * x的导数为f'(x) = 2 * x
        results.append(x)
    print('epoch 10, x:', x)
    return results

res = gd(0.2)

输出：

epoch 10, x: 0.06046617599999997

绘制出自变量 $x$ 的迭代轨迹

def show_trace(res):
    n = max(abs(min(res)), abs(max(res)), 10)
    f_line = np.arange(-n, n, 0.1)
    d2l.set_figsize()
    d2l.plt.plot(f_line, [x * x for x in f_line])
    d2l.plt.plot(res, [x * x for x in res], '-o')
    d2l.plt.xlabel('x')
    d2l.plt.ylabel('f(x)')

show_trace(res)

1.2 学习率

上述梯度下降算法中的正数 $\eta$ 通常叫作学习率。这是一个超参数，需要人工设定。如果使用过小的学习率，会导致 $x$ 更新缓慢从而需要更多的迭代才能得到较好的解。

下面展示使用学习率 $\eta =0.05$ 时自变量 $x$ 的迭代轨迹。可见，同样迭代10次后，当学习率过小时，最终 $x$ 的值依然与最优解存在较大偏差。

show_trace(gd(0.05))

输出：

epoch 10, x: 3.4867844009999995

如果设置过大的学习率，可能会导致最优解 $x=0$ 并逐渐发散。

show_trace(gd(1.1))

输出：

epoch 10, x: 61.917364224000096

1.3 多维梯度下降

在了解了一维梯度下降之后, 我们再考虑一种更广义的情况: 目标函数的输入为向量, 输出为标量。假设目标函数 $f:{\mathbb{R}}^d\to \mathbb{R}$ 的输入是一个 $d$ 维 向量 $\mathbf{x}={\left[x_1,x_2,\dots ,x_d\right]}^{\top }$ 。目标函数 $f(\mathbf{x})$ 有关 $\mathbf{x}$ 的梯度是一个由 $d$ 个偏导数组成的向量:

$${\nabla }_{x}f(x)={[\frac{\partial f(x)}{\partial x_1},\frac{\partial f(x)}{\partial x2},...,\frac{\partial f(x)}{\partial x_d}]}^T$$

因此，我们可能通过梯度下降算法来不断降低目标函数 $f$ 的值：

$$x\leftarrow x-\eta \nabla f(x)$$

下面我们构造一个输入为二维向量 $x=[x_1,x_2{]}^T$ 和输出为标量的目标函数 $f(x)=x_1^2+2x_2^2$。那么梯度 $\nabla f(x)=[2x_1,4x_2]$

def train_2d(trainer):  # 本函数将保存在d2lzh_pytorch包中方便以后使用
    x1, x2, s1, s2 = -5, -2, 0, 0  # s1和s2是自变量状态，本章后续几节会使用
    results = [(x1, x2)]
    for i in range(20):
        x1, x2, s1, s2 = trainer(x1, x2, s1, s2)
        results.append((x1, x2))
    print('epoch %d, x1 %f, x2 %f' % (i + 1, x1, x2))
    return results

def show_trace_2d(f, results):  # 本函数将保存在d2lzh_pytorch包中方便以后使用
    d2l.plt.plot(*zip(*results), '-o', color='#ff7f0e')
    x1, x2 = np.meshgrid(np.arange(-5.5, 1.0, 0.1), np.arange(-3.0, 1.0, 0.1))
    d2l.plt.contour(x1, x2, f(x1, x2), colors='#1f77b4')
    d2l.plt.xlabel('x1')
    d2l.plt.ylabel('x2')

然后，观察学习率为0.1时自变量的迭代轨迹。使用梯度下降对自变量 $x$ 迭代20次后，可见最终 $x$ 的值较接近最优解 $[0,0]$ 。

eta = 0.1

def f_2d(x1, x2):  # 目标函数
    return x1 ** 2 + 2 * x2 ** 2

def gd_2d(x1, x2, s1, s2):
    return (x1 - eta * 2 * x1, x2 - eta * 4 * x2, 0, 0)

show_trace_2d(f_2d, train_2d(gd_2d))

输出：

epoch 20, x1 -0.057646, x2 -0.000073

2. 随机梯度下降

在深度学习里，目标函数通常是训练数据集中有关各个样本的损失函数的平均。朴素的梯度下降根据目标函数 $f(x)$ 对所有样本梯度取平均，一轮结束之后再更新迭代 $x$。
$$\nabla f(x)=\frac{1}{n}\sum _{i=1}^n\nabla f_i(x)$$
$$x\leftarrow x-\eta \nabla f(x)$$

而随机梯度下降的每次迭代随机均匀取出一个样本索引 $i\in 1,...,n$，并计算梯度 $\nabla f_i(x)$ 来迭代 $x$：
$$x\leftarrow x-\eta \nabla f_i(x)$$

下面我们通过在梯度中添加均值为0的随机噪声来模拟随机梯度下降，以此来比较它与梯度下降的区别。

def sgd_2d(x1, x2, s1, s2):
    return (x1 - eta * (2 * x1 + np.random.normal(0.1)),
            x2 - eta * (4 * x2 + np.random.normal(0.1)), 0, 0)

show_trace_2d(f_2d, train_2d(sgd_2d))

输出：

epoch 20, x1 -0.047150, x2 -0.075628

可以看到，随机梯度下降中自变量的迭代轨迹相对于梯度下降中的来说更为曲折。这是由于实验所添加的噪声使模拟的随机梯度的准确度下降。在实际中，这些噪声通常指训练数据集中的无意义的干扰。

3. 小批量随机梯度下降

在每一次迭代中，梯度下降使用整个训练数据集来计算梯度，因此它有时也被称为批量梯度下降（batch gradient descent）。而随机梯度下降在每次迭代中只随机采样一个样本来计算梯度。正如我们在前几章中所看到的，我们还可以在每轮迭代中随机均匀采样多个样本来组成一个小批量，然后使用这个小批量来计算梯度。

$$g_t\leftarrow \nabla f_{B_t}(x_{t-1})=\frac{1}{|B|}\sum _{i\in B_t}\nabla f_i(x_{t-1})$$
$$x_t\leftarrow x_{t-1}-{\eta }_t{g}_t$$

小批量随机梯度下降中每次迭代的计算开销为 $O(|B|)$ 。当批量大小为1时，该算法即为随机梯度下降；当批量大小等于训练数据样本数时，该算法即为梯度下降。

pytorch 简洁实现

# 本函数与原书不同的是这里第一个参数优化器函数而不是优化器的名字# 例如: optimizer_fn=torch.optim.SGD, optimizer_hyperparams={"lr": 0.05}def train_pytorch_ch7(optimizer_fn, optimizer_hyperparams, features, labels,
                    batch_size=10, num_epochs=2):
    # 初始化模型
    net = nn.Sequential(
        nn.Linear(features.shape[-1], 1)
    )
    loss = nn.MSELoss()
    optimizer = optimizer_fn(net.parameters(), **optimizer_hyperparams)

    def eval_loss():
        return loss(net(features).view(-1), labels).item() / 2

    ls = [eval_loss()]
    data_iter = torch.utils.data.DataLoader(
        torch.utils.data.TensorDataset(features, labels), batch_size, shuffle=True)

    for _ in range(num_epochs):
        start = time.time()
        for batch_i, (X, y) in enumerate(data_iter):
            # 除以2是为了和train_ch7保持一致, 因为squared_loss中除了2
            l = loss(net(X).view(-1), y) / 2 

            optimizer.zero_grad()
            l.backward()
            optimizer.step()
            if (batch_i + 1) * batch_size % 100 == 0:
                ls.append(eval_loss())
    # 打印结果和作图
    print('loss: %f, %f sec per epoch' % (ls[-1], time.time() - start))
    d2l.set_figsize()
    d2l.plt.plot(np.linspace(0, num_epochs, len(ls)), ls)
    d2l.plt.xlabel('epoch')
    d2l.plt.ylabel('loss')
 
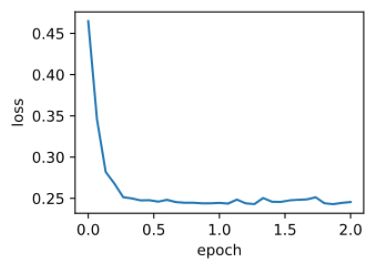
train_pytorch_ch7(optim.SGD, {"lr": 0.05}, features, labels, 10)

输出：

loss: 0.245491, 0.044150 sec per epoch

4. 动量法

梯度下降和随机梯度下降中我们提到，目标函数有关自变量的梯度代表了目标函数在自变量当前位置下降最快的方向。因此，梯度下降也叫作最陡下降（steepest descent）。在每次迭代中，梯度下降根据自变量当前位置，沿着当前位置的梯度更新自变量。然而，如果自变量的迭代方向仅仅取决于自变量当前位置，这可能会带来一些问题。

4.1 梯度下降的问题

让我们考虑一个输入和输出分别为二维向量 $x=[x_1,x_2{]}^T$ 和标量的目标函数 $f(x)=0.1x_1^2+2x_2^2$。下面实现基于这个目标函数的梯度下降，并演示使用学习率为 0.4 时自变量的迭代轨迹。

%matplotlib inline
import sys
sys.path.append("..") 
import d2lzh_pytorch as d2l
import torch

eta = 0.4 # 学习率

def f_2d(x1, x2):
    return 0.1 * x1 ** 2 + 2 * x2 ** 2

def gd_2d(x1, x2, s1, s2):
    return (x1 - eta * 0.2 * x1, x2 - eta * 4 * x2, 0, 0)

d2l.show_trace_2d(f_2d, d2l.train_2d(gd_2d))

输出：

epoch 20, x1 -0.943467, x2 -0.000073

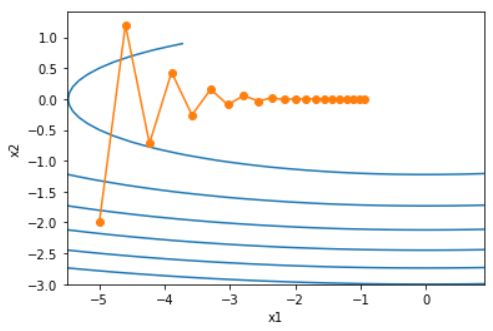
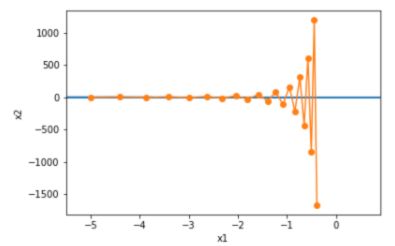
下面我们试着将学习率调得稍大一点，调成 0.6 ，此时自变量在竖直方向不断越过最优解并逐渐发散。

eta = 0.6
d2l.show_trace_2d(f_2d, d2l.train_2d(gd_2d))

输出：

epoch 20, x1 -0.387814, x2 -1673.365109

4.2 动量法

动量法的提出是为了解决梯度下降的上述问题。设时间步ttt的自变量为 $x_t$，学习率为 ${\eta }_t$。在时间步0，动量法创建速度变量 $v_0$，并将其元素初始化成0。在时间步 $t>0$，动量法对每次迭代的步骤做如下修改：
$$v_t\leftarrow \gamma v_{t-1}+{\eta }_t{g}_t$$
$${\text{x}}_t\leftarrow x_{t-1}-v_t$$

其中，动量超参数 $\gamma$ 满足 $0\le \gamma <1$ 。当 $\gamma =0$ 时，动量法等价于小批量随机梯度下降。

我们对动量法的速度变量做变形：
$$v_t\leftarrow \gamma v_{t-1}+(1-\gamma )(\frac{\eta \text{t}}{1-\gamma }{\text{g}}_t)$$
由质数加权移动平均的形式可得，速度变量 $v_t$ 实际上对序列 $\{\frac{{\eta }_{t-i}{g}_{t-i}}{1-\gamma }:i=0,...,\frac{1}{(1-\gamma )}-1\}$ 做了指数加权移动平均。换句话说，相比于小批量随机梯度下降，动量法在每个时间步的自变量更新量近似于将最近 $\frac{1}{1-\gamma }$个时间步的普通更新量(即学习率乘以梯度)做了质数加权移动平均后再除以 $1-\gamma$。

所以，在动量法中，自变量在各个方向上的移动幅度不仅取决当前梯度，还取决于过去的各个梯度在各个方向上是否一致。

4.3 从零开始实现

%matplotlib inline
import sys
sys.path.append("..") 
import d2lzh_pytorch as d2l
import torch

features, labels = d2l.get_data_ch7()

def init_momentum_states():
    v_w = torch.zeros((features.shape[1], 1), dtype=torch.float32)
    v_b = torch.zeros(1, dtype=torch.float32)
    return (v_w, v_b)

def sgd_momentum(params, states, hyperparams):
    for p, v in zip(params, states):
        v.data = hyperparams['momentum'] * v.data + hyperparams['lr'] * p.grad.data
        p.data -= v.data

d2l.train_ch7(sgd_momentum, init_momentum_states(),
              {'lr': 0.02, 'momentum': 0.5}, features, labels)

输出：

loss: 0.245518, 0.042304 sec per epoch

4.4 简洁实现

在 PyTorch 中，只需要通过参数 momentum 来指定动量超参数即可使用动量法。

%matplotlib inline
import sys
sys.path.append("..") 
import d2lzh_pytorch as d2l
import torch

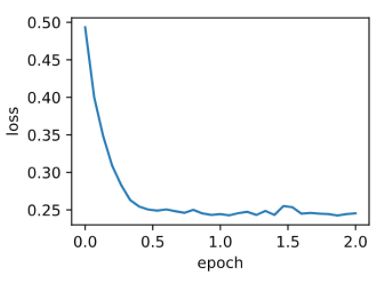
d2l.train_pytorch_ch7(torch.optim.SGD, {'lr': 0.004, 'momentum': 0.9}, features, labels)

输出：

loss: 0.253280, 0.060247 sec per epoch