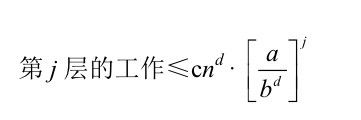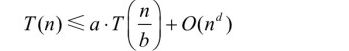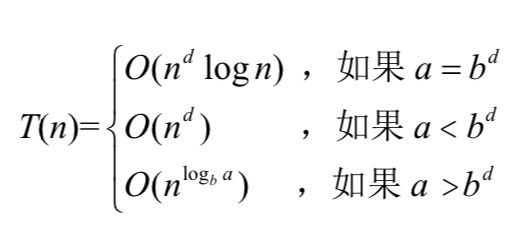递归算法复杂度与主定理的推导
一、基本概念
分治法的基本思想
分治法就是把一个大的问题分解成为若干个小的问题,求出小问题的解后合并即为大问题的解
分治法能够解决的问题的一般特征
- 该问题可以分解为若干规模规模较小的相同问题;
- 该问题的规模缩小到一定的程度就可以很容易的解决;
- 如果不满足的话就不必进行使用分治法进行分解了;
- 分解之后的子问题的解可以合并成为该问题的解;
- 该问题所分解出的各个子问题是相互独立的,即子问题之间不包含公共的子问题
二、分治法的时间复杂度的分析(主定理)
主定理是我们分析递归算法所需要的工具。 主定理将算法的递归过程作为输入,而其输出就是该算法的运行时间上界。
主定理的另一个版本—标准递归过程
如果T(n)被定义为一个标准地推过程,满足参数 a>=1,b>=1,d>=1,则
例如:在一个归并排序的递归过程中,一次二分需要调用两个递归过程,而这两次递归过程就是代表着a ,而每一次的递归都是将之前的数组一分为二,即长度便为原来的二分之一,则输入长度的收缩因子就是2,(b=2),在递归调用完成之后需要将完成之后合成一个整体返回,之后就是递归调用之外所需要的完成的工作,就归并排序为例他是线性的,所以d=1.因此:
a= 2=21=bd
满足上图Tn中的条件一,所以 T(n)=O(dnlog n) = O(n log n)
他的递归时间复杂度就是 O(n log n)
例如:二分搜索要么对输入数组的左半部分继续搜索,要么对右半部分继续搜索(不会同时对两者进行搜索),因此只有 1 个递归调用(a = 1)。 这个递归调用对输入数组的一半进行操作,因此 b 仍然等于 2。在递归调用之外, 二分搜索所执行的操作只是一个比较(数组中间元素的值与被搜索元素的值), 以决定下一步是在数组的左半部分还是右半部分进行搜索。因此递归调用之外的工作量是 O(1),所以 d = 1。由于 a = 1 = 20 = bd,所以还是满足主定理的第一种情况,所以运行时间上界是 O(nd log n) = O(log n)。
关于nd的解法分析
n的d次方是指把子问题的解合并的时间开销,你是可以确定的。它是根据你的实际问题来确定的。
例如:在归并排序中,你可以先假设你已经把左右两半都排好序了,于是在合并阶段你要做的事情是就是把左边的n/2个有序的数和右边n/2个有序的数 合并在一起使得n个数有序,这个合并两个有序表过程需要O(n),于是d=1.
三、主定理的推导
问题分解
在我们对 归并排序所进行的分析中,我们想要逐层计算递归算法所完成的工作。这个计划需要理解两个概念:某个特定的递归层 j 的不同子问题的数量以及每个子问题的输入长度。
受归并排序分析的启发,我们的计划是用一种分治算法对第 j 层子问题所执行的操作数量进行统计,然后把它累加上所有层次的工作上。现在,我们重点是观察归树的第 j 层。根据上图分析得到,第 j 层一共有 aj个不同的子问题, 每个子问题的输入长度为 n / bj。
把第 j 层所有 aj 个子问题累加起来就得到递归树的第 j 层所完成的工作量的上界:

我们把依赖于第 j 层的内容与不依赖第 j 层的内容分离开来,对这个表达式 进行简化:
不等式的右端最引人注目的是 a/bd 这个关键比率。a 与 bd的比值正好决定了其结果符合主定理的三种情况,所以不需要对分析过程中明确出现这个比率而感到惊讶,这正是我们想要的结果。
合并各层结果
一共有多少层呢?输入长度最初是 n,它在每一层的收缩因子是 b。由于我 们假定 n 是 b 的整数次方,当长度为 1 时就满足基本条件,因此递归树的层次正 好就是 n 不断除以 b 结果为 1 时的次数,也就是 logbn。把 j = 0, 1, 2, …, logbn 的所有层的工作相加就可以推导出下面这个神秘的运行时间上界(nd与j无关):

不管你是否相信,我们已经达成了证明主定理的一个重要里程碑。不等式 (4.4)的右端看上去有点像神秘的字母“大杂烩”,但是通过适当的解释,它正
是我们深入理解主定理的关键。
三种情况分析
正如上边推导出来的公式可以知道 其关键因素的是a/bd 这个关键比率。
- a:也就是每个 递归层的子问题增殖率(RSP),它是子问题数量爆炸性增长的扩张因子。
- bd:也就是工作量的收缩率(RWS),在递归的每一层,每个子问题的工作量都会根据收缩因子 bd 进行缩减。
那么工作量是会随着递归的层数增加而增加,还是随着递归的层数的增加而减少,又或者是每一层完成的工作量是相同的。
结论如下
- 如果 RSP < RWS,则递归层次 j 越深,它所完成的工作量就越少。
- 如果 RSP > RWS,则递归层次 j 越深,它所完成的工作量就越多。
- 如果 RSP = RWS,则每个递归层所完成的工作量都是相同的。
四、结语
收获
再次把结论放这里。在弄明白主定理是怎么回事之后,我想着大家只要记住公式的大致用法,以后再加以练习,在运用递归方法时候会更加的熟练,用的更加习惯。
学习过程
我在学习主定理的时候是先看了《算法详解》卷一–算法基础 前四章。
当时看完书不是特别明白,又去B站找了一个视频看了一下结合书本加以理解【学习记录】分治和主定理的推导-计算机算法_哔哩哔哩_bilibili
在看书和看视频之后,我对主定理的前两个参数(a,b) 有了会很好额理解,但是在面对第三个参数nd的时候还是不太清楚怎么算,什么是递归调用之外的工作量?我紧接着又去查了一下博客,在看博客的时候我复习了一下之前在书和视频中的内容,对书中遗漏的知识点,在这篇博客中算是的到了一个很好的补充。
那关于nd 我是在这篇博客中的评论里学到的,所以把那段评论也放在了我的文章里面。
博客如下:Master—Theorem 主定理的证明和使用_jmhIcoding-CSDN博客_master定理
引用
- 《算法详解》卷一 —算法基础 作者:
Tim Roughgarden - 【学习记录】分治和主定理的推导-计算机算法_哔哩哔哩_bilibili
- Master—Theorem 主定理的证明和使用_jmhIcoding-CSDN博客_master定理