挑战程序设计竞赛 练习日记
没用的碎碎念:2022.1.24:我又滚回来看算法了,仿佛回到了一年前……在学校摸鱼了一年,说实话什么都没学到,我的学校只是一个弱鸡一本,专业课程都很水,大一上学了c语言,大一下学了数据结构,大二上学了计算机网络,这就是目前为止一个大二计算机学生学的所有专业课。没了高三那股劲,越来越懒了,看着我以前高中那些985,211,或是一些普通的计算机一本大学的同学,挺担心自己的未来的,我觉得我竞争不过他们。我们学校专业分流了,我选了软件工程,没有什么特殊的原因,只是因为这个专业比计科课少罢了,想考研但是现在对自己没什么信心了,软件工程别人说挺好就业的,大概是为了给自己考不上研究生找了一条退路罢了……
上一年我参加了蓝桥杯,在突击了一个寒假的数据结构后,我拿了省二,今年的愿望,大概就是拿省一吧(做梦ing……),我发现了一本挺好的算法书,叫做《挑战程序设计竞赛》,我想这个寒假看一下里面的题目自己动手写一下,希望我能多勤奋点儿吧,其实寒假已经过了十几天了,这十几天我都在睡觉玩手机熬夜,真的看不下去这样的自己了,真的求求我自己能勤奋一点点吧……
备注:这里的代码不是书上的代码,是自己写的,书上的代码会比我的严谨简洁,这只是一篇小小的练习日记,用的是c和c++语言。
目录
- 第 1 章:蓄势待发——准备篇
-
-
- 三角形
- Ants(POJ 1852)
- 抽签
-
- 第 2 章:初出茅庐——初级篇
-
- 2.1 穷竭搜索
-
- 部分和问题
- Lake Counting (POJ 2386)
- 迷宫的最短路径
- Anagram(POJ 1256)
- Network Saboteur(POJ 2531)
- 2.2 贪心算法
-
- 硬币问题
- 区间调度问题
- Best Cow Line(POJ 3617)
- Saruman's Army (POJ 3069)
- Fence Repair (POJ 3253)
- 2.3 动态规划
-
- 01背包
- 最长公共子序列
- 完全背包
- Charm Bracelet (POJ 3624)
- 01背包 2
- 多重部分和
- 最长上升子序列
- 划分数
- 多重集组合数
- 2.4 数据结构
-
- Expedition (POJ 2431)
- Fence Repair (POJ 3253)
- Hardwood Species(POJ 2418)
- 航空公司VIP客户查询(PTA 7-45 数据结构与算法题目集)
- Double Queue (POJ 3481)
- 食物链(POJ 1182)
- 2.5 图论
-
- 二分图判定
- Roadblocks(POJ 3255)
- Conscription(POJ 3723)
- Layout(POJ 3169)
第 1 章:蓄势待发——准备篇
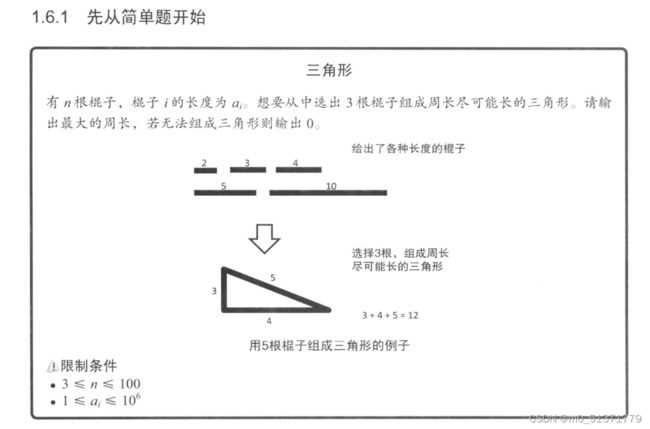
三角形
样例 2
输入
4
4 5 10 20
输出
0
思路:暴力枚举,枚举三条边长a,b,c,通过a+b>c判断是否能组成三角形,遍历找周长=a+b+c的最大值。
我的代码:
#include Ants(POJ 1852)
题目链接:http://poj.org/problem?id=1852
翻译:

输入
第一行整数 T,表示有 T 组测试数据
每组测试包含以下内容:
第一行两个整数,分别为 L,n,表示竿子长度和蚂蚁数量
第二行 n 个整数,表示每个蚂蚁距离左端点的距离 xi
输出
输出 T 行,每行两个整数,表示一组测试数据中所有蚂蚁落下竿子所需的最短时间和最长时间
样例 1
输入
2
10 3
2 6 7
214 7
11 12 7 13 176 23 191
输出
4 8
38 207
思路要点:蚂蚁是否反向不影响掉落时间,最短时间为每只蚂蚁最短时间的最长时间,最长时间为每只蚂蚁最长时间的最长时间(只有自己才能看懂的笔记,建议去看书上的推导)
心情:就挺巧妙的,没思考出来,本来我以为会很难的。
我的代码:
#include 抽签

输入
第一行输入整数 n
第二行输入整数 m
第三行输入 n 个整数,表示每个纸片上的数字 ki
输出
一行,Yes 或 No
样例 1
输入
3
10
1 3 5
输出
Yes
思路:
法一:暴力枚举 a+b+c+d,看是否等于m,时间复杂度O(n4)
法二:a+b+c+d=m 改写为 c+d=m-a-b,枚举m-a-b,看是否等于c+d。用数组cd存储c+d的所有值,在cd中利用二分法查找m-a-b,时间复杂度O(n4 logn)
心情:我之前认为一定都要枚举abcd才能算出来,没想到一个小小的公式变化就可以把时间复杂度大幅降低
我的代码
#include 第 2 章:初出茅庐——初级篇
2.1 穷竭搜索
部分和问题

输入
多组测试数据,以 EOF 结束
每组测试数据由以下部分组成:
第一行为整数 n
第二行为 n 个整数 ai
第三行为整数 k
数据保证多组测试数据的 n 之和不超过 20
输出
每组测试输出一行,Yes 表示能成功,No 表示失败
样例 1
输入
4
1 2 4 7
13
4
1 2 4 7
15
输出
Yes
No
思路:用dfs搜索
心情:感觉和上面抽签那题挺像的,但是抽签那题因为它可以重复选,所以用不了dfs,这题能用。好久没搞算法连dfs都写不熟练了,太搞笑了。
我的代码:
#include Lake Counting (POJ 2386)
题目链接:http://poj.org/problem?id=2386
翻译

输入
第一行两个整数 N,M,表示 N 行 M 列
接下来有 N 行,每行 M 个字符,可能是 ., W,. 表示地,W 表示水
输出
一个整数,表示多少个水洼
样例 1
输入
10 12
W…WW.
.WWW…WWW
…WW…WW.
…WW.
…W…
…W…W…
.W.W…WW.
W.W.W…W.
.W.W…W.
…W…W.
输出
3
思路:dfs遍历每个水洼,遍历过的W改为.,大的dfs次数即为水洼个数
心情:本来我的想法是不用dfs,从头到尾遍历园子,如果左,上,左上,右上有W则合并为一个水洼,否则水洼个数sum++。然后我的样例没过,但是现在的网站都不能显示没过的具体样例,我通过一行行打印把我没过的一个样例拼出来了,原来是我考虑问题不全面。因为如果出现(0,0),(1,1),(0,2)都是W的情况,我按顺序遍历到(0,2)时它会把自己视为一个水洼。我之前没用考虑到这种情况,所以调了好久。现在这题我懂了,开心,用dfs写也挺简单的,本来dfs那里八个方向我本来打算枚举来着,它的那个dx,dy还挺妙的,以后我遍历周围我也用这个。
我的代码:
#include 迷宫的最短路径

输入
第一行两个整数 N, M
接下来 N 行,每行 M 个字符,表示迷宫
输出
输出一行,表示从起点到终点的最少步数
样例 1
输入
10 10
#S######.#
…#…#
.#.##.##.#
.#…
##.##.####
…#…#
.#######.#
…#…
.####.###.
…#…G#
输出
22
思路:bfs搜索
心情:新学了一个pair,以前我用的是结构体。写代码时犯了两个错误:第一个是遍历上下左右四个方向时我用的时上一题Lake Counting的方法,然后忘记了那个方法是八连通的而本题只是四连通,要用回老方法两个数组。第二个是判断入队那里的条件我写的其中一个是MAP[nx][ny]!=‘.’ 然后忘记了终点是‘G’,我还纠结了半天为什么最后一步不行,好粗心哦,应该用 MAP[nx][ny]!='#'才对。
我的代码:
#include Anagram(POJ 1256)
题目链接:http://poj.org/problem?id=1256
Description
You are to write a program that has to generate all possible words from a given set of letters.
Example: Given the word “abc”, your program should - by exploring all different combination of the three letters - output the words “abc”, “acb”, “bac”, “bca”, “cab” and “cba”.
In the word taken from the input file, some letters may appear more than once. For a given word, your program should not produce the same word more than once, and the words should be output in alphabetically ascending order.
Input
The input consists of several words. The first line contains a number giving the number of words to follow. Each following line contains one word. A word consists of uppercase or lowercase letters from A to Z. Uppercase and lowercase letters are to be considered different. The length of each word is less than 13.
Output
For each word in the input, the output should contain all different words that can be generated with the letters of the given word. The words generated from the same input word should be output in alphabetically ascending order. An upper case letter goes before the corresponding lower case letter.
Sample Input
3
aAb
abc
acba
Sample Output
Aab
Aba
aAb
abA
bAa
baA
abc
acb
bac
bca
cab
cba
aabc
aacb
abac
abca
acab
acba
baac
baca
bcaa
caab
caba
cbaa
Hint
An upper case letter goes before the corresponding lower case letter.
So the right order of letters is ‘A’<‘a’<‘B’<‘b’<…<‘Z’<‘z’.
Source
Southwestern European Regional Contest 1995
思路:利用next_permutation
心情:这个不是这本书里面的题目,是我自己找来写的,因为这本书只是简单介绍了next_permutation,没用给具体的题目,我想应用一下新知识就额外写了这个题目。对了POJ不可以用万能头文件,好拉跨,我不想记那么多头文件呜呜。前几天我在csdn上看到了一篇挺好的关于next_permutation原理与用法的博客,但是我刚刚去找了很久都找不到了,怕我以后忘了,我大概用只有自己能理解的话说一下思路。 我的代码: 题目链接:http://poj.org/problem?id=2531 翻译和参考代码:https://blog.csdn.net/martin31hao/article/details/8098302 Input Output Sample Input Sample Output Source 题目大意:有n个点,把这些点分别放到两个集合里,在两个集合的每个点之间都会有权值,求可能形成的最大权值。 思路: 思路:在参考代码的基础上多加了剪枝思路的第一点(对称),但其实我没有完全对称,比如说6个数字,我只对称了12和3456这种数字个数不同的情况,没有考虑到123和456这种数字相同的对称,但我太懒了不想写了。 心情:这题也是我自己找的,书上介绍了剪枝但是没有给出例题,我自己找了这题做。剪枝思路的第二点卡了我挺久的,我不太理解为什么可以剪枝,我当时想是是否有移动一个点权值减少而移动两个点权值增加的情况。就比如说对于点1,2,3,4,5,先让1自己一组,移动2使1,2为一组,权值变小即1,2为一组的权值比1自己一组权值小,这时移动3使1,2,3为一组,这时1,2,3为一组的权值比1,3一组和1自己一组的权值都大,我总感觉会有这种情况。后来我亲自画图列了等式发现等式无解,即没有这种情况。我研究了一会儿把自己说服了,就是如果对于1自己一组时,移入2权值减少。那么对于1,3一组时,移入2权值也会减少。因为对于1自己一组移动2意味着减去12边加2的其他边,移入2总权值减少意味着边12的权值>2的其他边权值。那么对于1,3一组时,移入2意味着减去12和23边加2的其他边,由于边12的权值>2的其他边权,则容易推出边12的权值+边23的权值>2的其他边权,即减去的权值>加上的权值,故第二钟剪枝方法是正确的。 我的代码: 输出 样例 1 思路:贪心,用常识可以做出 心情:这题看的时候偷懒了,没有自己思考就先看了答案。我知道是贪心还有思路,但对于把我的思路转换为代码,我其实还没有整理好头绪,然后我就毫无防备的看到了代码,有点可惜。我觉得它的min用的挺好的,我自己思考的话应该想不到这样用,下次遇到问题我一定要先独立思考,再看答案和解析。 我的代码: 输出 样例 1 思路:贪心,在可选的工作中,每次选取结束时间最早的工作 心情:吸取了上一题的教训,我看到题目先自己思考了一会儿,然后,我完美踩坑,选了下面这个错误的算法 我的代码: 题目链接:http://poj.org/problem?id=3617 翻译 输出 样例 1 思路:贪心,尽量使用字典序小的字符,首尾字符相同时比较下一个字符 心情:考虑问题不全面,只想到了比较选小字符,没考虑字符相同的情况。意识到第一个字符相同时,只考虑了选第二个小字符,没有考虑第二个字符相同的情况。有了正确的思路后没有很好的转换成代码,S[l+j]>S[r-j]这个是借鉴书上的,挺巧妙的。 我的代码: ac截图:(我发现可以只截一个题目的,不过那个太小啦,我还是加上这个总的叭。没想到做了6题就有前10万了,开心) 题目链接:http://poj.org/problem?id=3069 翻译 输出 样例 1 思路:给所有的点排序,从左向右贪心选点 心情:刚开始看错题目了,以为标记的点可以是任意一点,然后样例那里手算了半天都是2而不是4。后来研究了一下别人的代码发现原来是从给出的点里面选标记点。我的思路和书上的思路差不多,但是写代码的方式有所不同,书上那个主用while,我对于if拿手一些。 我的代码:(没看参考代码前自己想的) 看了书上的代码后写的: 题目链接:http://poj.org/problem?id=3253 翻译: 输出 样例 1 思路:反过来想,给出各个木块长度,每次从里面拿两个木块拼起来,这样就容易想到,要想开销最小,每次应该选最短的两个木块。 心情:这是我上一年蓝桥杯海选的时候做过的题,我当时想了很久都没做出来,因为当时我只学了c语言的基本语法,连贪心这种基本词汇都很陌生。我在考场绞尽脑汁想了半天放弃了哈哈哈,当时我觉得这时一个挺有趣的小题目,印象挺深刻的。这题的时间还是卡得挺紧的,我刚开始选最小两个数的想法是每一次循环都用sort,然后取头两个数,好傻啊。后来我的想法是把遍历过的数变成无穷大,然后用两个for循环找最小的数,也好傻啊。我总是超时,纠结了半天,我看了书上的代码,原来用一个for循环就可以搞定了,我这个笨蛋。而且书上遍历过的直接放到后面,就可以每次缩小遍历的范围,我最傻了,刚开始的时候把遍历过的放在前面,然后就开始傻傻搞不清了。好啦好啦我还是很有收获的,我还捡回了swap,我好久没用这个了,都快忘记它了。 我的代码: 输出 样例 1 思路:记忆化搜索或者动态规划 心情:本来我的思路是用w/v求出性价比最高的物品,从大到小放入背包。但是物品不一定能刚好填满背包,最后的物品的选择让我挺纠结的。然后我就看了书上的思路,穷竭搜索的思想还挺朴素的,dp的时候我还能理解,把记忆化搜索转换成动态规划我也能理解。到最后那个专栏各种各样的dp把我整懵了,真灵活应用。研究了半天终于搞懂了,但是我觉得我很快就忘了哈哈哈。到最后我自己写代码的时候对这些思想的理解更加深刻,其实各种各样的dp的差别很小,就差那么一点点而已,但我理解的时候我确实搞了半天。我刚学会就迫不及待去POJ 3624写题了,结果超时了呜呜,我的算法之旅还是任重道远啊。 我的代码: 啊啊啊啊啊啊啊啊啊啊啊啊,我要气死啦,我刚刚写博客写到一半把电脑一盖去吃饭去了,然后,我等我吃完饭回来,发现我之前写的内容全部不见了……不见了……不见了!!!!!!啊啊啊啊啊啊,我今天一天写了个寂寞,现在我一点心情都没有了,找了一个多小时也没找回来,我直接简略的重写算了,我现在没有任何的心情……并且特别的暴躁…… 输出 样例 1 我的代码: 输出 样例 1 知识点:滚动数组n&1即n%2==1 题目链接:http://poj.org/problem?id=3624 翻译:意思和01背包一样,数据范围不一样 思路:滚动数组+动态规划,其余和01背包同 我的代码: 好了,终于补完了。一个下午只写了三道题,是不是特别的蠢,唉,只能相信勤能补拙了。 输出 样例 1 思路:动态规划。用老方法会爆内存,由于n和wi比较小,可以考虑换一下思路,即dp[i][j]代表前i个物品价值总和等于j时的min重量,最后从右到左遍历第一个dp[n][j]<=W即为所求。 心情:懒得看书,看视频学会的,感觉对于新的知识点看视频P4效率更高一点。今天的我已经不暴躁了,我又鼓起精神来刷题啦哈哈哈,昨晚没熬夜今天心情特别好。 我的代码: 输出 样例 1 思路:动态规划。dp[i][j]代表前i个数字中挑出和为j时剩下的max数字数。 心情:这题也是看视频的P5的思路的,偷懒ing……因为之前都是求min,max,没见过求等于的,就没有思路了,这个还挺巧的。我现在发现了,dp这类问题可以解决变量是3个的情况。背包问题的时候,变量是n,w,v,分别对应i,j,dp[i][j]。然后现在变量是n,m,a,K,然后n和a可以绑定,所以剩下n,K,m,分别对应i,j,dp[i][j]。本来我的思路是m对应j,然后没有写出来。后来我发现这些都不是乱对应的,比如背包问题的时候,每一个物品有选和不选两种思路,这两种思路必须有所体现在后面的i和j中。如果m对应j,则选和不选难以体现。 我的代码: 输入 输出 样例 1 思路:有好几种,最简单的是dp+二分,书上第二种方法,dp[i]表示长度为i的上升子序列的最后一个数字 心情:绞尽脑汁思考后独立写出来的dp题,虽然时间复杂度不够好,思考过程有很多小逻辑错误修修补补,但怎么说是我第一个自己写出来的dp题,后来我把书上的dp也看了一遍,写了一遍。书上的方法真的棒,棒棒棒棒棒。受上一题三个变量的影响,我这题也用了三个不同的意义代表i,j,dp[i][j]哈哈,然后我就不会化简了。我自己复现书上第二种方法的时候,发现自己二分掌握的不够好(一些小判定没理解到位,具体见代码注释),好多小细节还是没搞懂,现在搞懂了,但我觉得我很快就会忘记的hhh,只能靠多练加深记忆了。我还学会了用fill初始化,以前用的都是memset。 知识点1:lower_bound 在从小到大的排序数组中 lower_bound的底层实现 upper_bound的底层实现 知识点2:fill() 函数参数:fill(first,last,val); 知识点3:memset() 一般用来填充char型数组 我的代码: 输出 样例 1 思路:动态规划,dp[i][j]代表j个物品划分成i组的方案数%M。 心情:新的题型,这是有关计数问题的dp。自己想不出来,有点巧妙,看视频学会的,理解书上的思路后独立敲了一遍。学校延期开学了,有点开心,反正我在学校也是摸鱼,而且宿舍没网+各种水课限制了我学算法,在家可以更加心无旁骛的学算法,但愿我们学院不要开网课,开网课我也是挂机。 我的代码: 心情:看书+视频写的,我还用excel模拟了一个样例,这个代码我用了一点滚动数组,属实是写滚动数组写上瘾了。 我的代码: 题目链接:http://poj.org/problem?id=2431 输入 输出 样例 1 思路:优先序列。将A从大到小排序,一次性把油用完,路过的加油站的油放进优先序列里,没油了从优先序列里加最大的油,ans++。如果没到达终点优先序列就没油了则输出-1。 心情:刚开始看的时候我第一反应是用dp做的,dp[i][j]代表到达第i个加油站时加油了j次后的油。初始化dp[0][0]=P。用for (int i=1;i<=n+1;i++) for (int j=0;j<=i;j++)来递推dp。我想的是,dp[i][j]=max(加油,不加油),即 知识点:priority_queue 基本操作: 我的代码: 题目链接:http://poj.org/problem?id=3253 翻译: 输出 样例 1 思路:优先队列。把所有长度放进去,每次取最少的两个。 心情:因为之前写过了,所以这题很快搞出来了,之前写的慢就是纠结优先队列的问题,现在学了这个priority_queue,再也不纠结了。不得不说,优先队列是真的快,这题用优先队列写只用了79ms,之前我那个方法是547ms,绝了。 我的代码: ac截图: 题目链接:http://poj.org/problem?id=2418 Description Input Output Sample Input Sample Output 大致意思:按字典序输出字符串及出现频率。 思路:二叉搜索树,用map 。 心情:学了二叉搜索树,懂了基本的原理,想用一下,然后又没有题目,只能自己上网找了。这题我们大二上的实习也有一个类似的题目,好吧我刚刚看了一眼题目,也没有很类似,叫统计字母出现频率,也挺简单的。大一的时候基础没打好,关于字符串的处理不太熟练。这次学校海选的时候也有一题很简单的字符串处理的题目,我会写但没写成,花了一个小时在考场那里纠结字符串的输入和排序,菜死了真的。 知识点1:getline() 知识点2:map() set是一种关联式容器,其特性如下: map和set一样是关联式容器,它们的底层容器都是红黑树,区别就在于map的值不作为键,键和值是分开的。它的特性如下: 我的代码: 不少航空公司都会提供优惠的会员服务,当某顾客飞行里程累积达到一定数量后,可以使用里程积分直接兑换奖励机票或奖励升舱等服务。现给定某航空公司全体会员的飞行记录,要求实现根据身份证号码快速查询会员里程积分的功能。 输入格式: 输出格式: 输入样例: 思路:unordered_map 心情:这就是我们学校大二上的蓝桥杯海选题目之一,挺简单的,但是我当时不会map,几乎是现场手写二叉搜索树了,基础不好写了半天没写出来,今天把它做出来了还挺开心的。刚开始我用map做的时候超时了,参考了别人用unordered_map卡着时间限制300多ms过了,后来我看了另一篇博客说不要用cout和cin,用printf和scanf,我改了一下,居然80ms过了,这时间差的也太多了吧,天呐,感受了一波c语言的快速。 我的代码: 链接:http://poj.org/problem?id=3481 Description Input Output Sample Input 大致意思:0代表停止,1 k p 加入权值为p的事件k,2代表处理一件最高权值的事件,3代表处理一件最低权值的事件。输出要处理的事件。 思路:map或set 心情:血的教训告诉我,cout和cin真的比printf和scanf用的时间多。我第一次写的思路是对的,但因为用了cout和cin,超时了。刚开始我还怀疑是map的问题,把它改成set,然后还是超时。我在网上找别人通过的代码,对着思路一点点看,最后发现,没有毛病,我的思路一点毛病都没有。然后我开始了漫长的找不同,我对自己的cout和cin过于自信以至于刚开始我一直在改类似于把switch和case改成if和else之类的弱智不同。到最后除了输入输出不一样的时候,我才突然反应过来上一题我在心情里面写过的,printf和scanf比cout和cin省时间的问题。啊啊啊啊啊,我都要摔电脑了,浪费我时间。果然,我在第一次写的代码的基础上把所有的cout和cin替换成printf和scanf后,ac……当时,我的白眼已经快要翻到天花板上了。 我的代码: map+cout+cin: 题目链接:http://poj.org/problem?id=1182 Description Input Output Sample Input 思路:并查集。分类讨论,枚举所有情况(t的取值,xy是否在同一个并查集),总结出公式。 心情: 我觉得好难。第一次遇到这种需要自己总结出公式的题,挺难想到的,枚举所有情况找规律得公式这个操作另我有点迷惑。我比较懒,每次遇到需要枚举的题目就总会觉得自己是错的。 心情:以前邻接表我是用数组的,因为每一行的大小不一样我还烦恼过,现在用vector就可以解决了,开心。写代码的时候忘记了vecor输入数据用的是push_back,我直接当成数组用了,写成了G[x][G[x].size()]=y; 我的代码: 题目链接:http://poj.org/problem?id=3255 输出 样例 1 思路:Dijkstra变形,用dist2记录次短路 心情:时隔多年我终于回来刷题了,最近 我的代码: 题目链接:http://poj.org/problem?id=3723 输出 样例 1 5 5 8 5 5 10 思路:kruskal 心情:感觉我的kruskal挺麻烦的,好长的样子。写题目的时候看少了个条件,我还以为选的人会有多,就是选N个人,但是从大于N的人的里面选,然后我纠结了一会儿。书上说权值要取反,我感觉没必要哎,排序的时候从大到小排就可以了。 我的代码: 题目链接:http://poj.org/problem?id=3169 我的代码:
1.当从右到左依次增大时,没有下一个排列。比如4321没有下一个排列。
2.对于两个数字来说,求下一个排列的方法是交换两个数字。如12交换1和2得到下一个排列是21,21从右到左依次增大,没有下一个排列。
3.对于三个数字,先解决后两个数字,再解决三个数字。如123先解决23,由第2点知交换2和3得到下一个数字32,则123下一个数为132。32由第1点知没没有下一个排列,故考虑数字1。1只有和比1大的数交换才算是下面的排列,数字2和数字3都符合条件,由常识知道应该选较小的数字2,得到231,由常识知道2后面的数字要从左到右升序才算是下一个排列,故132的下一个排列是213。
4.依次类推2个数字,3个数字…… 大致步骤都是交换两个数字然后排序。如何找交换的两个数字呢,答案是从右到左找第一个左<右的,记录左(记为a)的位置要交换,再从右到左找第一个大于a的,记为b(a#include Network Saboteur(POJ 2531)
剪枝思路:https://www.docin.com/p-541362382.html?docfrom=rrela
Description
A university network is composed of N computers. System administrators gathered information on the traffic between nodes, and carefully divided the network into two subnetworks in order to minimize traffic between parts.
A disgruntled computer science student Vasya, after being expelled from the university, decided to have his revenge. He hacked into the university network and decided to reassign computers to maximize the traffic between two subnetworks.
Unfortunately, he found that calculating such worst subdivision is one of those problems he, being a student, failed to solve. So he asks you, a more successful CS student, to help him.
The traffic data are given in the form of matrix C, where Cij is the amount of data sent between ith and jth nodes (Cij = Cji, Cii = 0). The goal is to divide the network nodes into the two disjointed subsets A and B so as to maximize the sum ∑Cij (i∈A,j∈B).
The first line of input contains a number of nodes N (2 <= N <= 20). The following N lines, containing N space-separated integers each, represent the traffic matrix C (0 <= Cij <= 10000).
Output file must contain a single integer – the maximum traffic between the subnetworks.
Output must contain a single integer – the maximum traffic between the subnetworks.
3
0 50 30
50 0 40
30 40 0
90
Northeastern Europe 2002, Far-Eastern Subregion
1、把这两个集合标记为0和1,先默认所有点都在集合0里。
2、依次枚举每个点id,把每个点都放到集合1里去,这个时候就要调整集合的权值了,原来和id都在集合0里的点,要把权值加上;而在集合1里的点,要把权值减去。
3、权值调整完毕后,和ans比较,如果比ans要大, 调整ans。
4、如果放到集合1中,调整节点后的权值比放在集合0中要大,那么就默认这个点在集合1中,继续枚举下面的点进行DFS。最终是可以把最有状态都枚举出来的。#include 2.2 贪心算法
硬币问题

输入
第一行整数 T,表示有 T 组测试数据
每组测试数据占两行:
第一行,6 个整数,分别表示 C1, C5, C10, C50, C100, C500
第二行,1 个整数,表示 A
输出 T 行,每行一个整数,表示每组测试数据中,需要的最少硬币数
输入
1
3 2 1 3 0 2
620
输出
6#include 区间调度问题

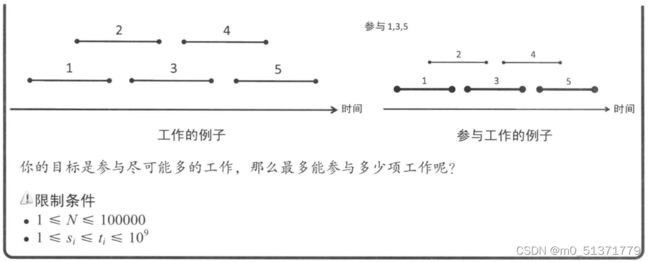
输入
多组测试数据,以 EOF 结束
每组测试:
第一行是整数 n
接下来 n 行,每行两个整数,表示一个工作的开始时间 si和 结束时间 ti
数据保证:多组测试数据的 n 总和不超过 105
输出多行,每行一个整数,表示一组测试数据中,最多能选多少个工作
输入
5
1 3
2 5
4 7
6 9
8 10
输出
3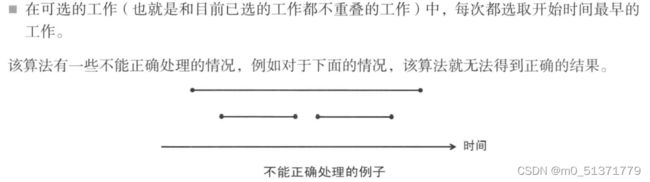
被自己傻到啦哈哈哈,真的挺巧妙的小逻辑,就差一点儿就得不到答案啦。#include Best Cow Line(POJ 3617)
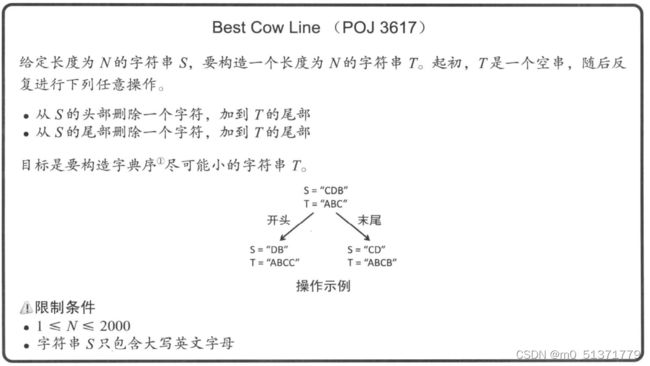
输入
第一行整数 N,表示 S 串的长度
接下来 N 行,每行一个大写英文字符,表示 S 串的每个字符
输出一行或多行:每行最多 80 个字符,当 T 串太长,需要换行再继续输出
输入
6
A
C
D
B
C
B
输出
ABCBCD#include
![]()
Saruman’s Army (POJ 3069)
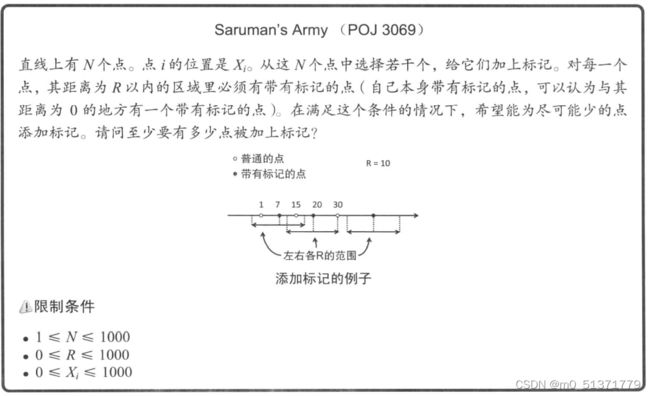
输入
多组测试数据,每组测试:
第一行两个整数 R和 N
第二行 N 个整数,用空格隔开,分别表示每个点的位置 xi
当 R = -1, N = -1 时表示输入结束
数据保证:多组数据的 N 总和不超过 105
每组测试数据输出一行,表示最少需要标记的点数
输入
0 3
10 20 20
10 7
70 30 1 7 15 20 50
-1 -1
输出
2
4#include #include Fence Repair (POJ 3253)

输入
第一行是整数 n,表示要将原始木板切割成多少块
接下来 n 行,每行一个整数,表示最终每块小木板的长度
一行,一个整数,表示达到目标所需的最小代价
输入
3
8
5
8
输出
34#include 2.3 动态规划
01背包

输入
输入数据第一行有两个整数 n 和 W,接下来会有 n 行,分别表示 n 个物品的对应的 wi和 vi
输出一个整数, 表示题目要求的最大价值
输入
4 5
2 3
1 2
3 4
2 2
输出
7//dp[i][j]代表前i个不超过j的max价值(记忆化搜索)(书上各种dp的第一个思路)
#include //dp[i][j]代表前i个不超过j的max价值(动态规划)(书上各种dp的第一个思路)
#include //dp[i][j]代表从第i个开始选择不超过j的max价值(记忆化搜索)(书上第一个思路)
#include //dp[i][j]代表从第i个开始选择不超过j的max价值(动态规划)(书上第一个思路)
#include //dp[i][j]代表前i个不超过j的max价值(记忆化搜索)(书上各种dp第二个思路)
#include //dp[i][j]代表前i个不超过j的max价值(动态规划)(书上各种dp第二个思路)
#include 最长公共子序列

输入
输入第一行有两个整数m和n,分别表示字符串s和t的长度,输入第二行和第三行分别表示字符串s和t.
对于每行输入,输出一行,包含一个整数,表示这两个字符串的最长公共子序列的长度.
输入
4 4
abcd
becd
输出
3//记忆化搜索
#include //动态规划
#include 完全背包

输入
输入数据第一行有两个整数 n 和 W,接下来会有 n 行,分别表示 n 个物品的对应的 wi和 vi
输出一个整数, 表示题目要求的最大价值.
输入
3 7
3 4
4 5
2 3
输出
10//记忆化搜索
#include //动态规划
#include //滚动数组
#include Charm Bracelet (POJ 3624)
#include 01背包 2

输入
输入数据第一行有两个整数 n 和 W,接下来会有 n 行,分别表示 n 个物品的对应的 wi和 vi
输出一个整数, 表示题目要求的最大价值
输入
4 5
2 3
1 2
3 4
2 2
输出
7#include //滚动数组
#include 多重部分和

输入
第一行包含两个整数 n 和 K
第二行包含 n 个数表示 a 数组
第三行一行包含 n 个数表示 m 数组
输出 Yes 或 No
输入
3 17
3 5 8
3 2 2
输出
Yes//自己写的原始版本
#include //看了书上参考代码后修改的
#include 最长上升子序列
第一行为一个整数 n
第二行有 n 个整数表示序列 a
一个整数,表示最长上升子序列的长度
输入
5
4 2 3 1 5
输出
3
链接1:https://blog.csdn.net/weixin_43939593/article/details/105602530
链接2:https://blog.csdn.net/qq_40160605/article/details/80150252
lower_bound( begin,end,num):从数组的begin位置到end-1位置二分查找第一个大于或等于num的数字,找到返回该数字的地址,不存在则返回end。通过返回的地址减去起始地址begin,得到找到数字在数组中的下标。
upper_bound( begin,end,num):从数组的begin位置到end-1位置二分查找第一个大于num的数字,找到返回该数字的地址,不存在则返回end。通过返回的地址减去起始地址begin,得到找到数字在数组中的下标。int lower_bound(vector<int>& nums, int x) {
int left = 0;
int right = nums.size() - 1;
while (left <= right) {
int mid = left +(right - left) / 2;
if (x > nums[mid]) {
left = mid + 1;
}
else {
right = mid - 1;
}
}
return left;
}
int upper_bound(vector<int>& nums, int x) {
int left = 0;
int right = nums.size() - 1;
while (left <= right) {
int mid = left +(right - left) / 2;
if (x >= nums[mid]) { //这里是大于等于
left = mid + 1;
}
else {
right = mid - 1;
}
}
return left;
}
first 首地址,last为尾地址,val为将要替换的值(可以赋任何值)。
链接:https://blog.csdn.net/qq_44711190/article/details/121124113
int型数组,只能填充0、-1 和 inf(正负都行)。//自己想的:dp[i][j]代表遍历前i个元素,子序列长度为j的子序列的最后一个数字
//时间复杂度:O(n^2)
#include //书上第二种思路:二分,dp[i]表示长度为i的上升子序列的最后一个数字
//我把书上lower_bound的二分详细写了
#include //书上第二种思路:dp[i]表示长度为i的上升子序列的最后一个数字
//时间复杂度:O(nlogn)
#include //书上第一种思路:dp[i]代表子序列以a[i]为末尾的子序列长度
//时间复杂度:O(n^2)
#include 划分数
输出一个整数表示划分方法数模 M 的余数
输入
4 3 10000
输出
4#include 多重集组合数

思路:动态规划。dp[i][j]代表从前i类物品中取出j个的取法数。配套视频有更直观的推导,这里直接理解。dp[i][j]=再选一个第i类物品+不选。不选=dp[i-1][j]。选=能选或不能选。能选=dp[i][j-1]。不能选即在dp[i][j-1]的时候已经把第i类物品用完了(j-a[i]-1<0), 所以在dp[i][j-1]的基础上减去把第i类物品用完的情况(即减去第i类物品选ai个的情况),即不能选=dp[i][j-1]-dp[i-1][j-a[i]-1]#include 2.4 数据结构
Expedition (POJ 2431)
第一行是 N,表示有多少个加油站
接下来 N 行,每行两个整数 Ai, Bi ,表示每个加油站距离终点的位置,以及最多可以加多少油
最后一行是 L, P
一个整数,表示最少加多少次油
输入
4
4 4
5 2
11 5
15 10
25 10
输出
2
dp[i][j]=max(dp[i-1][j] - 两个加油站的距离,dp[i-1][j-1] - 两个加油站的距离+b[i])。考虑边界,就是if (j==0) dp[i][j]=dp[i-1][j] - 两个加油站的距离;else if (dp[i-1][j-1] - 两个加油站的距离< 0 ) dp[i][j]=dp[i-1][j] - 两个加油站的距离;最终结果是从左至右遍历dp[n+1][j]的第一个>=0的j即为答案。这个方法我用excel算的样例能过,表格差不多是下图这样的(我把负数都写成-1了)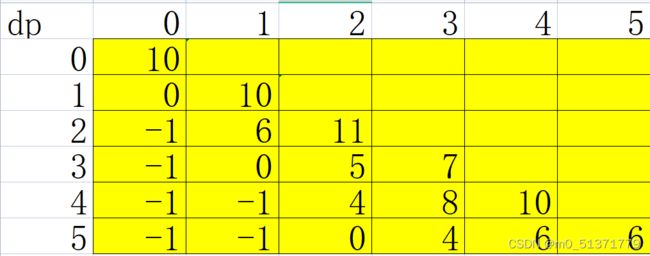
答案是2没有毛病,但是我没有把这个思路转换成代码,因为我看了时间限制是1000ms,我这个方法时间复杂度是O(N2),应该是会超时的。所以我就直接看书上的方法了,书上的方法好妙啊,今天又学到了新的知识priority_queue。有时候换换角度就可以省好多时间。复现书上的代码我用了pair,第一次WA了,因为它的a和b是不按大小顺序给的,要自己重新排,于是我就用pair sort了一下,就能过了。
链接:https://blog.csdn.net/weixin_36888577/article/details/79937886
(我今天学会了把csdn的长链接改短的方法了,就是复制一下博客的内容,粘贴后最下面版权申明那里有短的链接)
top 访问队头元素
empty 队列是否为空
size 返回队列内元素个数
push 插入元素到队尾 (并排序)
emplace 原地构造一个元素并插入队列
pop 弹出队头元素
swap 交换内容用法:
//升序队列
priority_queue <int,vector<int>,greater<int> > q;
//降序队列
priority_queue <int,vector<int>,less<int> >q;
#include Fence Repair (POJ 3253)

输入
第一行是整数 n,表示要将原始木板切割成多少块
接下来 n 行,每行一个整数,表示最终每块小木板的长度
一行,一个整数,表示达到目标所需的最小代价
输入
3
8
5
8
输出
34#include
![]()
Hardwood Species(POJ 2418)
Hardwoods are the botanical group of trees that have broad leaves, produce a fruit or nut, and generally go dormant in the winter.
America’s temperate climates produce forests with hundreds of hardwood species – trees that share certain biological characteristics. Although oak, maple and cherry all are types of hardwood trees, for example, they are different species. Together, all the hardwood species represent 40 percent of the trees in the United States.
On the other hand, softwoods, or conifers, from the Latin word meaning “cone-bearing,” have needles. Widely available US softwoods include cedar, fir, hemlock, pine, redwood, spruce and cypress. In a home, the softwoods are used primarily as structural lumber such as 2x4s and 2x6s, with some limited decorative applications.
Using satellite imaging technology, the Department of Natural Resources has compiled an inventory of every tree standing on a particular day. You are to compute the total fraction of the tree population represented by each species.
Input to your program consists of a list of the species of every tree observed by the satellite; one tree per line. No species name exceeds 30 characters. There are no more than 10,000 species and no more than 1,000,000 trees.
Print the name of each species represented in the population, in alphabetical order, followed by the percentage of the population it represents, to 4 decimal places.
Red Alder
Ash
Aspen
Basswood
Ash
Beech
Yellow Birch
Ash
Cherry
Cottonwood
Ash
Cypress
Red Elm
Gum
Hackberry
White Oak
Hickory
Pecan
Hard Maple
White Oak
Soft Maple
Red Oak
Red Oak
White Oak
Poplan
Sassafras
Sycamore
Black Walnut
Willow
Ash 13.7931
Aspen 3.4483
Basswood 3.4483
Beech 3.4483
Black Walnut 3.4483
Cherry 3.4483
Cottonwood 3.4483
Cypress 3.4483
Gum 3.4483
Hackberry 3.4483
Hard Maple 3.4483
Hickory 3.4483
Pecan 3.4483
Poplan 3.4483
Red Alder 3.4483
Red Elm 3.4483
Red Oak 6.8966
Sassafras 3.4483
Soft Maple 3.4483
Sycamore 3.4483
White Oak 10.3448
Willow 3.4483
Yellow Birch 3.4483
链接:https://blog.csdn.net/qq_25245961/article/details/77414134
作用:接受一个字符串,可以接收空格并输出#includewhile (getline(cin,s));//常用
链接:https://blog.csdn.net/ETalien_/article/details/89439892
先是书上的解释:


#include 航空公司VIP客户查询(PTA 7-45 数据结构与算法题目集)
输入首先给出两个正整数N和K。其中K是最低里程,即为照顾乘坐短程航班的会员,航空公司还会将航程低于K公里的航班也按K公里累积。随后N行,每行给出一条飞行记录。飞行记录的输入格式为:18位身份证号码(空格)飞行里程。其中身份证号码由17位数字加最后一位校验码组成,校验码的取值范围为0~9和x共11个符号;飞行里程单位为公里,是(0, 15 000]区间内的整数。然后给出一个正整数M,随后给出M行查询人的身份证号码。
对每个查询人,给出其当前的里程累积值。如果该人不是会员,则输出No Info。每个查询结果占一行。
4 500
330106199010080419 499
110108198403100012 15000
120104195510156021 800
330106199010080419 1
4
120104195510156021
110108198403100012
330106199010080419
33010619901008041x
输出样例:
800
15000
1000
No Info#include Double Queue (POJ 3481)
The new founded Balkan Investment Group Bank (BIG-Bank) opened a new office in Bucharest, equipped with a modern computing environment provided by IBM Romania, and using modern information technologies. As usual, each client of the bank is identified by a positive integer K and, upon arriving to the bank for some services, he or she receives a positive integer priority P. One of the inventions of the young managers of the bank shocked the software engineer of the serving system. They proposed to break the tradition by sometimes calling the serving desk with the lowest priority instead of that with the highest priority. Thus, the system will receive the following types of request:
0 The system needs to stop serving
1 K P Add client K to the waiting list with priority P
2 Serve the client with the highest priority and drop him or her from the waiting list
3 Serve the client with the lowest priority and drop him or her from the waiting list
Your task is to help the software engineer of the bank by writing a program to implement the requested serving policy.
Each line of the input contains one of the possible requests; only the last line contains the stop-request (code 0). You may assume that when there is a request to include a new client in the list (code 1), there is no other request in the list of the same client or with the same priority. An identifier K is always less than 106, and a priority P is less than 107. The client may arrive for being served multiple times, and each time may obtain a different priority.
For each request with code 2 or 3, the program has to print, in a separate line of the standard output, the identifier of the served client. If the request arrives when the waiting list is empty, then the program prints zero (0) to the output.
2
1 20 14
1 30 3
2
1 10 99
3
2
2
0
Sample Output
0
20
30
10
0//set
#include //map
#include
![]()
map+scanf+printf:(时间瞬间减少了1/3,从此对cout cin无爱……)
![]()
set+scanf+printf:
![]()
食物链(POJ 1182)
动物王国中有三类动物A,B,C,这三类动物的食物链构成了有趣的环形。A吃B, B吃C,C吃A。
现有N个动物,以1-N编号。每个动物都是A,B,C中的一种,但是我们并不知道它到底是哪一种。
有人用两种说法对这N个动物所构成的食物链关系进行描述:
第一种说法是"1 X Y",表示X和Y是同类。
第二种说法是"2 X Y",表示X吃Y。
此人对N个动物,用上述两种说法,一句接一句地说出K句话,这K句话有的是真的,有的是假的。当一句话满足下列三条之一时,这句话就是假话,否则就是真话。
1) 当前的话与前面的某些真的话冲突,就是假话;
2) 当前的话中X或Y比N大,就是假话;
3) 当前的话表示X吃X,就是假话。
你的任务是根据给定的N(1 <= N <= 50,000)和K句话(0 <= K <= 100,000),输出假话的总数。
第一行是两个整数N和K,以一个空格分隔。
以下K行每行是三个正整数 D,X,Y,两数之间用一个空格隔开,其中D表示说法的种类。
若D=1,则表示X和Y是同类。
若D=2,则表示X吃Y。
只有一个整数,表示假话的数目。
100 7
1 101 1
2 1 2
2 2 3
2 3 3
1 1 3
2 3 1
1 5 5
Sample Output
3#include 2.5 图论
二分图判定

思路:先给一个点涂颜色1,遍历相邻点涂颜色-1,继续遍历相邻点的相邻点直到遍历完图为止。出现矛盾则输出No。#include Roadblocks(POJ 3255)

输入
第一行有两个整数 N 和 R
接下来的 R 行,每行有三个整数 x, y, D,表示 x 和 y 之间有一条边长度为 D 的路径
次短路的长度
输入
4 4
1 2 100
2 3 250
2 4 200
4 3 100
输出
450好懒 好忙,专业课太多了没什么时间刷题。今天已经2022.3.29了,还有几天就比赛了,然而我上一次更这篇博客大概是两周前。最短路的那几个算法我到现在还没写熟练,菜菜。#include Conscription(POJ 3723)

输入
第一行整数 T,表示有多少组测试数据
每组测试数据最开始先是一个空行,再接着以下的部分:
第一行有 3 个整数 N 和 M 和 R
接下来的 R 行,每行均表示一条人际关系,三个整数 x, y, d, 表示女兵 x 和男兵 y 的关系值为 d
输出 T 行,每行一个整数,表示该组测试数据中所需的最小费用
输入
2
4 3 6831
1 3 4583
0 0 6592
0 1 3063
3 3 4975
1 3 2049
4 2 2104
2 2 781
2 4 9820
3 2 6236
3 1 8864
2 4 8326
2 0 5156
2 0 1463
4 1 2439
0 4 4373
3 4 8889
2 4 3133
输出
71071
54223#include Layout(POJ 3169)


思路:Bellman-Ford求最短路。假设j>i,d[i]代表i的位置,由题意知dj-di<=w好,dj-di>=w坏即di-dj<=-w 。类比最短路算法d3<=d1+10,d2<=d3-3 (样例)可知d[n]即为所求。负环输出-1,走不通输出-2 。
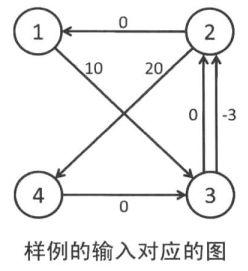
心情:在-1和-2的判断那里纠结了半天,对于图论我觉得我还是不太熟悉,要多练。#include