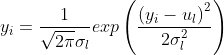智能系统专业实验(二):MRF图像分割实验
- 实验目的
掌握马尔科夫随机场(MRF)的算法原理,通过 Markov 随机场(MRF)实现图像的分割。
- 实验基本原理及步骤(或方案设计及理论计算)
(1)基本原理
令L和D是两个符号集:![]() ,
,![]() 。
。![]() 是下标集合,令X和Y是两个随机场,他们的状态空间分别是L和D,这样对于
是下标集合,令X和Y是两个随机场,他们的状态空间分别是L和D,这样对于![]() 有
有![]() 。令x表示X的一组配置,
。令x表示X的一组配置,![]() 是所有可能配置的集合,即
是所有可能配置的集合,即![]() ;同样,令y是Y的一组配置,y是所有可能配置的集合,则可得
;同样,令y是Y的一组配置,y是所有可能配置的集合,则可得![]() 。用X表示图像类别标识,Y表示图像灰度。
。用X表示图像类别标识,Y表示图像灰度。
MRF理论
MRF理论提供了建模上下文依赖实体的一种方式,实体包括图像像素和相关特征等。在MRF中,S中的位置通过邻域系统相互关联,邻域系统定义为![]() ,这里
,这里![]() 是位置 i 的邻域集,
是位置 i 的邻域集,![]() 。如果满足以下条件:
。如果满足以下条件:
则随机场X是S上关于邻域系统N的一个马尔科夫随机场(MRF)。由Hammersley-Clifford定理,MRF能够等价描述为Gibbs分布,则有
![]() (2)
(2)
这里Z是归一化常数;![]() 为能量函数,
为能量函数,![]() 为所有可能基团C的基团势能
为所有可能基团C的基团势能![]() 之和,一个基团C被定义为S中位置的子集,
之和,一个基团C被定义为S中位置的子集,![]() 的值依赖于基团C的局部配置。
的值依赖于基团C的局部配置。
MRF-MAP估计
令![]() 是图像真实标号的估计,由最大后验概率(MAP)准则有
是图像真实标号的估计,由最大后验概率(MAP)准则有
![]() (3)
(3)
由式(3)可知,要得到![]() ,需要首先计算类别的先验概率和观测量的似然概率。
,需要首先计算类别的先验概率和观测量的似然概率。
由于x被认为是MRF的一个实现,则他的先验概率表示为式(2)。又由准似然估计,式(2)可近似表示为
由Potts模型有:![]()
![]() ,则
,则
在给定类别标号![]() 时,通常认为像素强度值
时,通常认为像素强度值![]() 服从参数为
服从参数为![]() 高斯分布,
高斯分布,
基于最大后验概率(MAP)准则的图像分割,就是求标记集X,使得关于X的后验概率分布最大。考虑计算效率问题,采用条件迭代模式(ICM)方法。ICM算法是一个迭代算法,通过逐元的最大化条件概率实现像元值更新,即:
(2)算法步骤
- 变量说明
![]() 像素点 i 的类别标号;
像素点 i 的类别标号;
![]() 像素点 i 的像素值;
像素点 i 的像素值;
L 最大类别数;
D 像素最大取值(灰度图像为255);
![]() 第l类区域的均值;
第l类区域的均值;
![]() 第l类区域的标准方差;
第l类区域的标准方差;
![]() 平滑参数(取值通常在0.8 – 1.4);
平滑参数(取值通常在0.8 – 1.4);
![]() 像素点 i 的邻域。
像素点 i 的邻域。
迭代过程
Step1:给定图像初始分割(通过阈值法或聚类方法);
Step2:由当前分割更新![]() ,
,![]() 和
和![]() 分别是当前第 l 类区域的均值和标准方差;
分别是当前第 l 类区域的均值和标准方差;
Step3:由当前图像参数和上次迭代的分割结果,并根据式(7)计算每一点最大可能的类别;
Step4:判断是否收敛或达到了最高迭代次数,如果满足则退出;否则返回Step2,进行下一次迭代。
- 实验结果分析及回答问题(或测试环境及测试结果)
- 原图
- 聚类结果图
如上图最终聚类结果图,本次实验一共设置了三个聚类中心。初始分割由阈值法确定,所以最大迭代次数需要设置的更大一些。
- 实验代码
#include
#include
#include
#include
#include
#define max_pixel 99999999
#define max_k 50
#define imageW 320
#define imageH 240
unsigned char L[3] = {0, 1, 2};
unsigned char classes[imageH][imageW];
float p_w[imageW*imageH][3];
float p_s_w[imageW*imageH][3];
int ave[3];
float sig[3];
int num[3];
int bmpHeight, bmpWidth, biBitCount, k_num;
int label[max_pixel],rec[max_k];
int center[max_k][3];
unsigned char *pBmpBuf;
RGBQUAD *pColorTable;
void mrf(int image[],int h,int w,int itr){
unsigned int i, j, k, l;
unsigned maxiter = 20;
for(i = 0; i < w*h; i++){
unsigned int r = i / w;
unsigned int c = i % w;
classes[r][c] = image[i] / 86;
}
for(i = 0; i < maxiter; i++){
//计算P(w)
for(j = 0; j < w*h; j++){
unsigned int r = j / w;
unsigned int c = j % w;
for(l = 0; l < 3; l++){
p_w[j][l] = 0;
if(r >= 1 && c >= 1){
if(classes[r][c] != classes[r-1][c-1]){
p_w[j][l] -= 1;
}
}
if(r >= 1){
if(classes[r][c] != classes[r-1][c]){
p_w[j][l] -= 1;
}
}
if(r >= 1 && c + 1 < w){
if(classes[r][c] != classes[r-1][c+1]){
p_w[j][l] -= 1;
}
}
if(c + 1 < w){
if(classes[r][c] != classes[r][c+1]){
p_w[j][l] -= 1;
}
}
if(r + 1 < h && c + 1 < w){
if(classes[r][c] != classes[r+1][c+1]){
p_w[j][l] -= 1;
}
}
if(r + 1 < h){
if(classes[r][c] != classes[r+1][c]){
p_w[j][l] -= 1;
}
}
if(r + 1 < h && c >= 1){
if(classes[r][c] != classes[r+1][c-1]){
p_w[j][l] -= 1;
}
}
if(c >= 1){
if(classes[r][c] != classes[r][c-1]){
p_w[j][l] -= 1;
}
}
p_w[j][l] = 0 - 0.99 * p_w[j][l];
p_w[j][l] = exp(p_w[j][l]);
}
for(l = 0; l < 3; l++){
float sum = p_w[j][0] + p_w[j][1] + p_w[j][2];
p_w[j][l] = p_w[j][l] / sum;
}
}
//计算p_s_w
for(l = 0; l < 3; l++){
ave[l] = 0;
sig[0] = 0;
num[l] = 0;
}
for(j = 0; j < h; j++){
for(k = 0; k < w; k++){
for(l = 0; l < 3; l++){
if(l == classes[j][k]){
ave[l] += image[j * imageW + k];
num[l] += 1;
}
}
}
}
for(l = 0; l < 3; l++){
ave[l] /= num[l];
}
for(j = 0; j < h; j++){
for(k = 0; k < w; k++){
for(l = 0; l < 3; l++){
if(l == classes[j][k]){
sig[l] += pow((image[j * w + k] - ave[l]), 2);;
}
}
}
}
for(l = 0; l < 3; l++){
sig[l] /= num[l];
}
for(j = 0; j < w*h; j++){
for(l = 0; l < 3; l++){
p_s_w[j][l] = 0;
p_s_w[j][l] = 1 / (sqrt(2*3.14) * sqrt(sig[l]));
p_s_w[j][l] = p_s_w[j][l] * exp(-pow(image[j] - ave[l], 2) / sig[l]);
}
}
for(j = 0; j < w*h; j++){
for(l = 0; l < 3; l++){
p_w[j][l] = p_w[j][l] * p_s_w[j][l];
}
}
float maxVal = 0;
for(j = 0; j < w*h; j++){
unsigned int r = j / w;
unsigned int c = j % w;
for(l = 0; l < 3; l++){
if(maxVal < p_w[j][l]){
classes[r][c] = l;
maxVal = p_w[j][l];
}
}
}
}
ave[0]=62;ave[1]=157;ave[2]=228;
for(i = 0; i < h; i++){
for(j = 0; j < w; j++){
for(l = 0; l < 3; l++){
if(classes[i][j] == l){
image[i * w + j] = ave[l];
break;
}
}
}
}
}
int main(){
const char src[] = "lena.bmp";
const char dst[] = "segResultTest.bmp";
k_num = 3;
memset(label, 0, sizeof(label));
memset(center, 0, sizeof(center));
memset(rec, 0, sizeof(rec));
//读取 bmp 文件
FILE *fp = fopen(src, "rb");
if (fp == 0)
return 0;
fseek(fp, sizeof(BITMAPFILEHEADER), 0);
BITMAPINFOHEADER head;
fread(&head, 40, 1, fp);
bmpHeight = head.biHeight;
bmpWidth = head.biWidth;
biBitCount = head.biBitCount;
fseek(fp, sizeof(RGBQUAD), 1);
int LineByte = (bmpWidth*biBitCount / 8 + 3) / 4 * 4;
pBmpBuf = new unsigned char[LineByte*bmpHeight];
fread(pBmpBuf, LineByte*bmpHeight, 1, fp);
fclose(fp);
//将 24 位真彩图灰度化并保存
FILE *fp1 = fopen(dst, "wb");
if (fp1 == 0)
return 0;
int LineByte1 = (bmpWidth * 8 / 8 + 3) / 4 * 4;
//修改文件头,其中有两项需要修改,分别为 bfSize 和 bfOffBits
BITMAPFILEHEADER bfhead;
bfhead.bfType = 0x4D42;
bfhead.bfSize = 14 + 40 + 256 * sizeof(RGBQUAD)+LineByte1*bmpHeight;
bfhead.bfReserved1 = 0;
bfhead.bfReserved2 = 0;
bfhead.bfOffBits = 14 + 40 + 256 * sizeof(RGBQUAD);//修改偏移字节数
fwrite(&bfhead, 14, 1, fp1); //将修改后的文件头存入 fp1;
BITMAPINFOHEADER head1;
head1.biBitCount = 8; //将每像素的位数改为 8
head1.biClrImportant = 0;
head1.biCompression = 0;
head1.biClrUsed = 0;
head1.biHeight = bmpHeight;
head1.biWidth = bmpWidth;
head1.biPlanes = 1;
head1.biSize = 40;
head1.biSizeImage = LineByte1*bmpHeight;//修改位图数据的大小
head1.biXPelsPerMeter = 0;
head1.biYPelsPerMeter = 0;
fwrite(&head1, 40, 1, fp1); //将修改后的信息头存入 fp1;
pColorTable = new RGBQUAD[256];
for (int i = 0; i < 256; i++){
pColorTable[i].rgbRed = i;
pColorTable[i].rgbGreen = i;
pColorTable[i].rgbBlue = i; //是颜色表里的 B、G、R 分量都相等,且等于索引值
}
fwrite(pColorTable, sizeof(RGBQUAD), 256, fp1); //将颜色表写入 fp1
//写位图数据
unsigned char *newBmp;
newBmp = new unsigned char[LineByte1*bmpHeight];
int c = 0;
for (int i = 0; i < bmpHeight * bmpWidth;i++,c++)
label[i] = -1;
int rgbMap[bmpHeight * bmpWidth][3];
for (int i = 0; i < bmpHeight;i++){ //取位图 rgb 三通道数据
for (int j = 0; j < bmpWidth;j++){
unsigned char *tmp;
tmp = pBmpBuf + i * LineByte + j * 3;
rgbMap[i * bmpWidth + j][0] = int(*(tmp));
rgbMap[i * bmpWidth + j][1] = int(*(tmp+1));
rgbMap[i * bmpWidth + j][2] = int(*(tmp+2));
}
}
int image[bmpHeight*bmpWidth];
for (int i = 0; i < bmpHeight * bmpWidth;i++){
image[i] = rgbMap[i][0]*0.299 + rgbMap[i][1]*0.587 + rgbMap[i][2]*0.114;
}
mrf(image, bmpHeight, bmpWidth,30);
for (int i = 0; i < bmpHeight; i++){
for (int j = 0; j < bmpWidth; j++){
unsigned char *pb;
pb = newBmp + i * LineByte1 + j;
*pb = image[i * bmpWidth + j];
}
}
fwrite(newBmp, LineByte1*bmpHeight, 1, fp1);
fclose(fp1);
system("pause");
return 0;
}
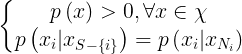
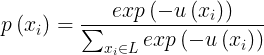
![\large u\left ( x_{i} \right )=-\beta _{i}\sum _{c\in C}V_{c}\left ( x_{i} \right )=-\beta _{i}\sum _{j\in N_{i}}\left [ \delta \left ( x_{i},x_{j} \right )-1 \right ]](http://img.e-com-net.com/image/info8/ff271a763f4b4b02913d92d6c010f7b6.gif)