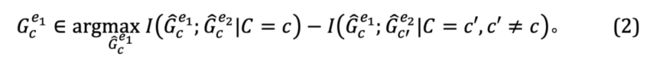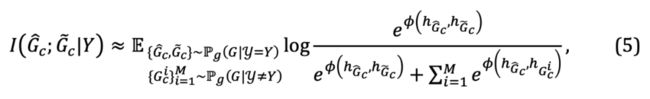NeurIPS 2022 | 面向图数据分布外泛化的因果表示学习

©作者 | Yongqiang Chen

引言

机器学习困境：相关性≠因果性

随着深度学习模型的应用和推广，人们逐渐发现模型常常会利用数据中存在的虚假关联（Spurious Correlation）来获得较高的训练表现。但由于这类关联在测试数据上往往并不成立，因此这类模型的测试表现往往不尽如人意 [1]。其本质是由于传统的机器学习目标（Empirical Risk Minimization，ERM）假设了训练测试集的独立同分布特性，而在现实中该独立同分布假设成立的场景往往有限。

在很多现实场景中，训练数据的分布与测试数据分布通常表现出不一致性，即分布偏移（Distribution Shifts），旨在提升模型在该类场景下性能的问题通常被称为分布外泛化（Out-of-Distribution Generalization）问题。

关注学习数据中的相关性而非因果性的 ERM 等一类方法往往难以应对分布偏移。尽管近年涌现了诸多方法借助因果推断（Causal Inference）中的不变性原理（Invariance Principle）在分布外泛化问题上取得了一定的进展，但在图数据上的研究依然有限。这是因为图数据的分布外泛化比传统的欧式数据更加困难，给图机器学习带来了更多的挑战。

本文以图分类任务为例，对借助因果不变性原理的图分布外泛化进行了探究。

主题图片

近年来，借助因果不变性原理，人们在欧式数据的分布外泛化问题中取得了一定的成功，但对图数据的研究仍然有限。与欧式数据不同，图的复杂性对因果不变性原理的使用以及克服分布外泛化难题提出了独特的挑战。

为了应对该挑战，我们在本工作中将因果不变性融入到图机器学习中，并提出了因果启发的不变图学习框架，为解决图数据的分布外泛化问题提供了新的理论和方法。论文已在 NeurIPS 2022 发表并入选了会议的 Spotlight Presentation（比例约 5%），本工作由香港中文大学、香港浸会大学、腾讯 AI Lab 以及悉尼大学合作完成。

论文标题：

Learning Causally Invariant Representations for Out-of-Distribution Generalization on Graphs

论文链接：

https://openreview.net/forum?id=A6AFK_JwrIW

项目代码：

https://github.com/LFhase/CIGA

图数据的分布外泛化

1.1 图数据的分布外泛化难在哪？

图神经网络近年来在涉及图结构的机器学习应用，如推荐系统、AI 辅助制药等领域，取得了很大的成功。然而，因现有的大部分的图机器学习算法都依赖于数据的独立同分布假设，使得当测试数据和训练数据出现分布偏移时，算法的性能会极大下降。同时，因为图数据结构的复杂性，导致图数据的分布外泛化相比于欧式数据更普遍且更具挑战性。

▲ 图1. 图上的分布偏移示例

首先，图数据的分布偏移可以出现在图的节点特征分布中（Attribute-level Shifts）。例如，在推荐系统中，训练数据涉及的商品可能采自一些比较流行的类别，涉及到的用户也可能来自于某些特定地区，而在测试阶段，系统则需要妥善处理所有类别以及地区的用户和商品 [2,3,4]。此外，图数据的分布偏移还可以出现在图的结构分布中（Structure-level Shifts）。

早在 2019 年，人们就注意到，在较小的图上进行训练得到的图神经网络难以学到有效的注意力（Attention）权重以泛化到更大的图上 [5]，这也推动了一系列相关工作的提出 [6,7]。

在现实场景中，这两类分布偏移往往可能同时出现，并且这些不同层级的分布偏移还可以和所要预测的标签具有不同的虚假关联模式。如在推荐系统中，来自特定类别的商品与特定地区的用户往往会在商品用户交互图上展现独特的拓扑结构 [4]。在药物分子属性预测中，训练时涉及的药物分子可能偏小，同时预测的结果也会受到实验测定环境的影响 [8]。

此外，欧式空间的分布外泛化往往会假设数据来自于多个环境（Environment）或者域（Domain），并进一步假设训练期间模型能够获取训练数据中每个样本所属的环境，以此来发掘跨越环境的不变性。

然而，要获得数据的环境标签往往需要和数据相关的一些专家知识，而由于图数据的抽象性，使得图数据的环境标签获得更加昂贵。因此，大部分现有的图数据集如 OGB 都不含此类环境标签信息，即便少部分如 DrugOOD 数据集存在环境标签，但也存在不同程度的噪声 [8]。

1.2 现有方法能否解决图上的分布外泛化问题？

为了对图数据分布外泛化的挑战有一个直观的理解，我们基于 Spurious-Motif [9] 数据集构建新的数据以进一步实例化上述几大挑战，并尝试使用现有的方法如欧式数据上分布外泛化的训练目标 IRM [10]，或者具有更强表达能力的 GNN [11]，分析能否通过已有的方法解决图数据的分布外泛化问题。

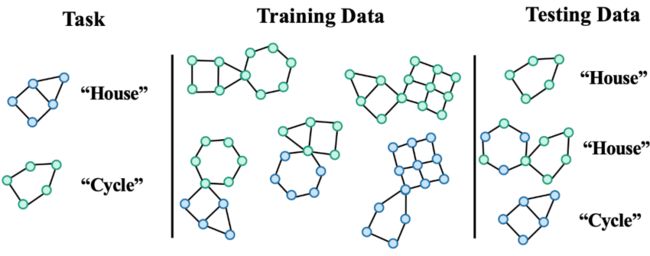
▲ 图2. Spurious Motif 数据集示例

Spurious Motif 任务如图2所示，主要根据输入的图中是否含有特定结构的子图（如 House，或者 Cycle）对图标签进行判断，其中节点颜色代表节点的属性。使用该数据集可以比较清晰地测试不同层级的分布偏移对图神经网络性能的影响。对于一个使用 ERM 进行训练的普通 GNN 模型：

• 如果训练阶段大部分有 House 子图的样本都节点大部分绿色，而 Cycle 则是蓝色，那么在测试阶段，模型则倾向于预测任何含大量绿色节点的图为“House”，而蓝色节点的图为“Cycle”。

• 如果训练阶段大部分有 House 子图的样本都与一个六边形子图共同出现，那么在测试阶段，模型则倾向于判定任何含有六边形结构的图为“House”。

此外，模型在训练时无法获得任何和环境标签相关的信息，得到实验结果如图 3 所示（更多结果可以查阅论文附录 D）。

▲ 图3. 现有方法在不同图分布偏移下的表现

如图 3 所示，普通的 GCN 不论是在使用 ERM 或者 IRM 训练，都无法应对图的结构偏移（Struc）；而在增加了图节点属性偏移（Mixed）以及图大小分布偏移后（即图 3 后两幅图），模型性能将进一步降低；此外即便使用具有更强表达能力的 kGNN 也难以避免严重的性能损失（平均性能的降低，或更大的方差）。

由此，我们自然地引出所要研究的问题：如何才能获得一个具有应对多种图分布偏移的 GNN 模型？

面向图数据分布外泛化的因果模型

为了解决上述问题，我们需要对学习目标，即不变图神经网络（Invariant GNN），进行定义，即在最糟糕的环境下仍旧表现良好的模型（严谨的定义参见论文）：

定义1（不变图神经网络）给定一系列收集自不同的具有因果关联的环境 的图分类数据集 ，其中 包含被认为是来自环境 的独立同分布样本，考虑一个图神经网络 ，其中 和 分别是作为输入的图空间和样本空间，我们称 是不变图神经网络，当且仅当 ，即最小化所有环境的最坏经验损失（worst empirical risk），其中 为模型在环境 中的经验损失。

模型在训练时只能获得部分的训练环境 中的数据，如果不对数据的过程进行任何假设，不变图神经网络定义所要求的 minmax 最优性是很难做到的。因此，我们从因果推断的角度使用因果模型（Structural Causal Model）对图的生成过程进行建模，并对环境之间的关联进行刻画，以尝试定义图数据上的因果不变性。

▲ 图4. 图数据生成过程的因果模型

不失一般性，我们将所有影响图生成的隐变量纳入隐空间 ，并将图的生成过程建模为 。此外，对于隐变量 ，根据其是否受环境 影响，我们将其划分成不变隐变量（invariant latent variable） 以及虚假隐变量（spurious latent variable）。对应地，隐变量 与 分别会影响 的某个子图的生成，分别记作不变子图 以及虚假子图 ，如图 4（a）所示。

图的标签 则主要取决于 所蕴含的信息，这也可以进一步推出 ，即 与 相比于 有更高的互信息。这样的生成过程与许多实际例子相对应，如一个分子的药化属性通常由某个关键的基团（分子子图）决定（如羟基-HO 之于分子的水溶性）。

此外， 与 以及 在隐空间有多种类型的交互，主要跟进虚假隐变量 与标签 是否在有不变隐变量 之外额外的关联，即 ⫫，可以概括为两种：如图 4（b）的FIIF（Fully Informative Invariant Feature）以及图 4（c）的 PIIF（Partially Informative Invariant Feature）。其中 FIIF 表示给定不变信息后标签与虚假相关量独立。PIIF 则相反。

需要说明的是，为了尽可能地覆盖更多的图分布偏移，我们的因果模型致力于对各种图生成模型的广泛的建模。如有更多关于图生成过程的知识，图 4 所示的因果模型则可以进一步泛化到更具体的例子。如在附录 C.1 中，我们展示了如何通过增加额外图极限（graphon）的假设，将因果图泛化至先前 Bevilacqua 等人用于分析图大小分布偏移的工作 [7]。

基于上述的因果分析，我们可以知道，当模型只使用不变子图 进行预测的时，即只使用 之间的关联，模型的预测才不会受到环境 的改变而影响；反之，如果模型的预测依赖于任何与 或 有关的信息，其预测结果将会因为 E 的变化发生极大的改变，从而出现性能损失。

因此，我们的目标可以从学习一个不变图神经网络，进一步细化至：a）识别潜在的不变子图；b）用识别的子图预测 。为了进一步与数据生成的算法过程相对应，我们进一步把图神经网络 拆分为子图识别网络（Featurizer GNN） 和分类网络（Classifier GNN），且 ，其中 为 的子图空间。那么模型的学习目标则可表示为如公式（1）所示：

其中，，为子图识别网络对不变子图的预测； 为 与 的互信息，通常，最大化 可以通过最小化使用 预测 的经验损失实现。然而，由于 的缺失，我们难以直接使用 对 进行独立性 ⫫ 的验证，为此，我们必须寻求其他等价条件以识别需要的不变子图。

因果启发的不变图学习

为了解决在缺失 E 时的不变子图识别问题，基于公式（1）的框架，我们希望寻求一个公式（1）的易于实现的等价条件。特别地，我们首先考虑一种比较简单的情况，即潜在的不变子图大小固定且已知，。在这样的条件下，考虑最大化 ，尽管 与 有同样的大小，但因为 与 也存在关联，所以在没有任何其他约束的情况下，最大化 可能会使得估计得到的不变子图中包含部分与 有互信息的虚假子图。

为了将 中可能的虚假子图部分“挤”出去，我们将进一步从因果模型中寻求更多关于 特有的属性。注意到，不论是 PIIF 还是 FIIF 的虚假关联类型，对于最大化与标签 互信息的子图，我们有：

• 不同环境 中与相同不变隐变量 的不变子图是这两个环境中互信息最大的两个子图，即，；

• 同一个环境 中对应不同不变隐变量 的不变子图两个不变子图是这个环境中互信息最小的两个子图，即，；

结合上述两个性质，我们可以推出

由于在实践中我们难以直接观察得到 ，我们则可以通过 作为 在公式（2）中的代理使用。同时，当 和 同时达到最大化时， 将自动最小化，否则模型的预测将坍缩至平凡解。

由此，我们得到了在一种简单情况下的不变子图等价条件，结合公式（1），我们得到了第一版因果启发的不变图学习（Causality-inspired Invariant Graph leArning）框架，即 CIGAv1：

其中， 且 ，即 与 来自同个类别 。我们在论文中进一步证明了 CIGAv1 在已知图大小情况下能成功识别图 4 对应的因果模型中潜在的不变子图。

然而，由于先前的假设过于理想化，在实践中，不变子图的大小可能会发生改变同时对应的大小我们也往往无法得知。在没有子图大小的假设下，只需要将全图识别为不变子图即能满足 CIGAv1 的要求。因此，我们考虑进一步寻求关于不变子图别的性质用于去除这一假设。

注意到，在最大化 时，可能出现 中的虚假子图部分与被去除的不变子图部分享有同样的和 相关的互信息。那么，我们能否反其道而行之，同时最大化 以去除 中可能的虚假子图部分呢？

答案是肯定的，我们可以利用 与 的关联令其与 的估计互相竞争。需要注意的是，在最大化 时需要保证 不会超过 ，否则将预测的 又将陷入平凡解。结合这一额外的条件，我们则可以将关于不变子图大小的假设从公式（3）去除，得到如下 CIGAv2：

▲ 图5. 因果启发的不变图学习框架示意

CIGA 的实现：在实践中，估计两个子图的互信息通常比较困难，而监督式的对比学习 [11] 则提供了一种可行的解法：

其中 对应着公式（4）中的正样本，而 则是对应于 的图表示。当 时，公式（5）提供了对于 的一种基于 von Mises-Fisher kernel density的非参数再代入熵估计（Nonparameteric Resubstitution Entropy Estimator ）[13,14]。

最终 CIGA 核心部分的实现如图 5 所示，即通过在隐表示空间拉近同个类别不变子图的图表示，同时最大化不同类别不变子图的图表示，以最大化 。此外，对于公式（4）中的另一个约束，我们则可以通过铰链损失（hinge loss）的思路进行实现，即 ，只优化预测 时经验损失大于对应的不变子图的虚假子图。

实验与讨论

在实验中，我们使用 16 个合成或来自真实世界的数据集，对 CIGA 在不同图分布偏移下进行了充分的验证。在实验中，我们使用可解释 GNN 框架 [9] 实现了 CIGA 的原型，而实际上 CIGA 有更多实现的方式。具体的数据集以及实验细节详见文中实验部分。

4.1 合成数据集上图结构分布偏移以及混合分布偏移的表现

我们首先基于 SPMotif 数据集 [9] 构造了 SPMotif-Struc 以及 SPMotif-Mixed 数据集，其中 SPMotif-Struc 包含了特定子图与图中其他子图结构的虚假关联，以及图大小的分布偏移；而 SPMotif-Mixed 则在 SPMotif-Struc 的基础上新增了图节点属性层级的分布偏移。

表中第一栏为 ERM 以及可解释 GNN 的基线，第二栏则为欧式空间最先进的分布外泛化算法。从结果中可以发现，不论是更好的 GNN 框架还是欧式空间的分布外泛化算法，都受制于图上的分布偏移，且当更多的分布偏移出现时，性能损失（更小的平均分类性能或更大的方差）将进一步增强。相对的，CIGA 则能在不同强度的分布偏移下保持良好的性能，并极大超越最好的基线表现。

4.2 真实数据集上各类图分布偏移的表现

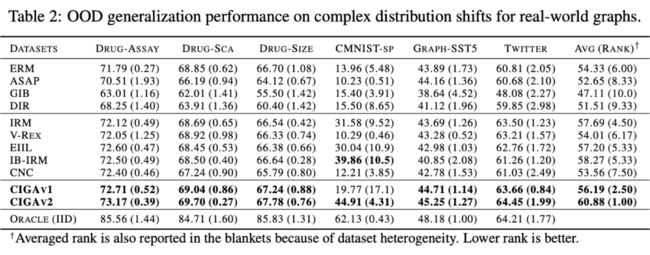
我们接着在真实数据集和各种真实数据中存在的图分布偏移进一步测试了 CIGA 的表现，包括来自 AI 辅助制药中药物分子属性预测的 DrugOOD 中三种不同环境划分（实验环境 Assay，分子骨架 Scaffold，分子大小 Size）的三个数据集，包含了各种真实应用场景的图分布偏移。

基于欧式空间中经典的图像数据集 ColoredMNIST [10] 转换得到的 CMNIST-SP，主要包含图节点属性的 PIIF 类型分布偏移；基于自然语言情感分类数据集 SST5 以及 Twitter 转化得到的 Graph-SST5 以及 Twitter [15]，并且额外添加了图度数的分布偏移。此外，我们还使用了先前研究较多的4个分子图大小分布偏移数据集 [7]，

测试结果如上表所示，可以发现，在真实数据中，由于任务难度增加，使用更好架构的 GNN 或者欧式空间的分布外泛化优化目标训练得到的模型性能甚至弱于使用 ERM 训练得到的普通 GNN 模型。这一现象也与欧式空间中更难任务下的分布外泛化实验观察得到的现象类似 [16]，反应了真实数据上的分布外泛化难度以及现有方法的不足。

与之相对地，CIGA 则能在所有的真实数据和图分布偏移上获得提升，甚至在某些数据集如 Twitter、PROTEINS 中达到经验最优的 Oracle 水准。在最新的图分布外泛化测试基准 GOOD 上图分类数据集的初步测试也显示了CIGA是目前最好且能应对各种个样的图分布偏移的图分布外泛化算法。

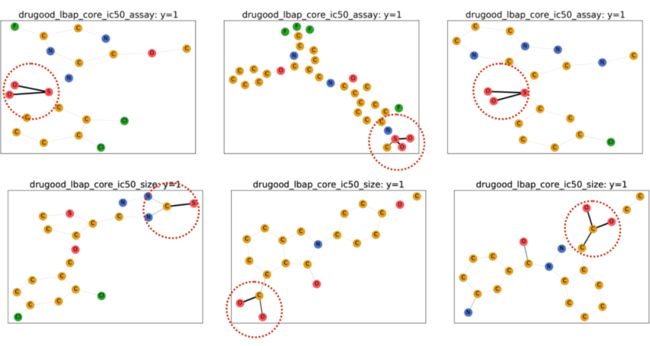
由于使用了可解释 GNN 作为 CIGA 的原型实现架构，我们也对模型识别得到的 DrugOOD 中的进行了可视化，发现 CIGA 确实发现了一些比较一致的分子基团用于分子属性预测。这可以为后续 AI 辅助制药提供更好的依据。

▲ 图6. DrugOOD中CIGA识别得到的部分不变子图

总结及展望

本文通过因果推断的角度，首次将因果不变性引入至多种图分布偏移下的图分布外泛化问题中，并提出了一个全新的具有理论保证的解决框架 CIGA。大量实验也充分验证了 CIGA 优秀的分布外泛化性能。

放眼未来，基于 CIGA，我们可以进一步探索更好的实现框架 [17]，或为 CIGA 引入更好的具有理论保障的数据增强方法 [3,18]，并在理论上建模纳入图上的协变量偏移（Covariate Shift）[19]，以进一步提升 CIGA 识别不变子图的能力，促进图神经网络在 AI 辅助制药等真实应用场景的真实落地使用。

参考文献

[1] Zhang et al., CausalAdv: Adversarial Robustness Through the Lens of Causality, ICLR 2022.

[2] Zhu et al., Shift-Robust GNNs: Overcoming the Limitations of Localized Graph Training Data, NeurIPS 2021.

[3] Wu et al., Handling Distribution Shifts on Graphs: An Invariance Perspective, ICLR 2022.

[4] Chen et al., Bias and Debias in Recommender System: A Survey and Future Directions, TOIS 2022.

[5] Boris et al., Understanding Attention and Generalization in Graph Neural Networks, NeurIPS 2019.

[6] Gilad et al., From Local Structures to Size Generalization in Graph Neural Networks, ICML 2021.

[7] Bevilacqua et al., Size-Invariant Graph Representations for Graph Classification Extrapolations, ICML 2021.

[8] Ji et al., DrugOOD: OOD Dataset Curator and Benchmark for AI-aided Drug Discovery, arXiv 2022.

[9] Wu et al., Discovering Invariant Rationales for Graph Neural Networks, ICLR 2022.

[10] Arjovsky et al., Invariant Risk Minimization, arXiv 2020.

[11] Morris, et al., Weisfeiler and leman go neural: Higher-order graph neural networks, AAAI 2019.

[12] Khosla et al., Supervised contrastive learning, NeurIPS 2020.

[13] Wang and Isola, Understanding contrastive representation learning through alignment and uniformity on the hypersphere, ICML 2020.

[14] Ahmad and Lin, A nonparametric estimation of the entropy for absolutely continuous distributions (corresp.), IEEE Transactions on Information Theory, 22(3):372–375, 1976.

[15] Hao et al., Explainability in Graph Neural Networks: A Taxonomic Survey, arXiv 2021.

[16] Gulrajani and Lopez-Paz, In Search of Lost Domain Generalization, ICLR 2021.

[17] Miao et al., Interpretable and Generalizable Graph Learning via Stochastic Attention Mechanism, ICML 2022.

[18] Yu et al., Finding Diverse and Predictable Subgraphs for Graph Domain Generalization, arXiv 2022.

[19] Gui et al., GOOD: A Graph Out-of-Distribution Benchmark, NeurIPS 2022 Datasets and Benchmarks.

更多阅读

#投 稿 通 道#

 让你的文字被更多人看到 

如何才能让更多的优质内容以更短路径到达读者群体，缩短读者寻找优质内容的成本呢？答案就是：你不认识的人。

总有一些你不认识的人，知道你想知道的东西。PaperWeekly 或许可以成为一座桥梁，促使不同背景、不同方向的学者和学术灵感相互碰撞，迸发出更多的可能性。 

PaperWeekly 鼓励高校实验室或个人，在我们的平台上分享各类优质内容，可以是最新论文解读，也可以是学术热点剖析、科研心得或竞赛经验讲解等。我们的目的只有一个，让知识真正流动起来。

 稿件基本要求：

• 文章确系个人原创作品，未曾在公开渠道发表，如为其他平台已发表或待发表的文章，请明确标注 

• 稿件建议以 markdown 格式撰写，文中配图以附件形式发送，要求图片清晰，无版权问题

• PaperWeekly 尊重原作者署名权，并将为每篇被采纳的原创首发稿件，提供业内具有竞争力稿酬，具体依据文章阅读量和文章质量阶梯制结算

 投稿通道：

• 投稿邮箱：[email protected] 

• 来稿请备注即时联系方式（微信），以便我们在稿件选用的第一时间联系作者

• 您也可以直接添加小编微信（pwbot02）快速投稿，备注：姓名-投稿

△长按添加PaperWeekly小编

现在，在「知乎」也能找到我们了

进入知乎首页搜索「PaperWeekly」

点击「关注」订阅我们的专栏吧

·

·