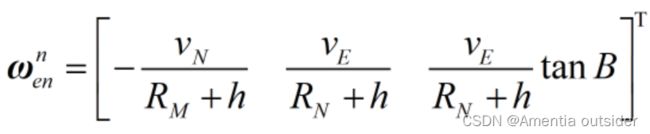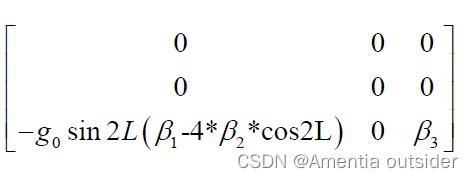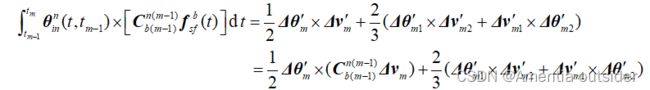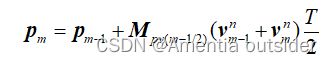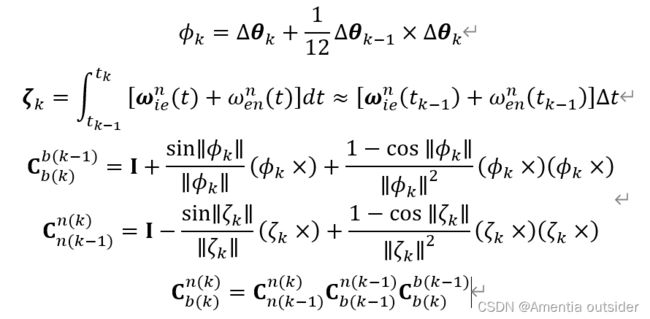GNSS/INS组合导航学习-GINAV（一）

从今天开始整理一下，最近半年学习的组合导航算法

目前开源程序

1、严老师PSINS工具箱 （MATLAB——卡尔曼滤波算法)

2、GINAV （MATLAB——卡尔曼滤波算法 ）

3、KF-GINS （C++——卡尔曼滤波算法）

当然也有图优化算法，后续有时间会继续整理的。参考书：严老师的捷联惯导与卡尔曼滤波原理、武汉大学牛老师组合导航算法讲义，分别对以上三个程序详细整理。

注意：采取的坐标系不同，捷联惯导程序也会有所不同。（东北天与北东地）

GINAV

分别有以下12个文件夹

 今天主要整理ins文件夹

 INS_1——askew.m

function matrix = askew(vector)
% convert 3x1 vector to 3x3 askew matrix.

matrix = [        0,  -vector(3),   vector(2);
          vector(3),           0,  -vector(1);
         -vector(2),   vector(1),           0];
return      

这个是最常见的反对称矩阵

知识点：反对称矩阵是正规矩阵、反对称的幂方通式、反对称的矩阵指数函数

matrix 3*3的矩阵 vector是 3*1的矩阵

INS_2——att2Cnb.m

function Cnb = att2Cnb(att)

sina=sin(att); cosa=cos(att);
sinp=sina(1);  sinr=sina(2); siny=sina(3);
cosp=cosa(1);  cosr=cosa(2); cosy=cosa(3);
Cnb=[ cosr*cosy-sinp*sinr*siny, -cosp*siny,  sinr*cosy+sinp*cosr*siny;
      cosr*siny+sinp*sinr*cosy,  cosp*cosy,  sinr*siny-sinp*cosr*cosy;
                    -cosp*sinr,       sinp,                 cosp*cosr];

return

将欧拉角转换为方向余弦

航向角y：运载体纵轴在当地水平面上的投影线与当地地理北向的夹角，常取北偏东为正角度范围为0～360°

俯仰角p：运载体纵轴与其水平投影线之间的夹角，当运载体抬头时角度定义为正，角度范围-90°～90°，

横滚角r：运载体立轴与纵轴所在铅垂面之间的夹角，当运载体向右倾斜时角度定义为正，角度范围-180°～180°

INS_3——Cnb2att.m

function att = Cnb2att(Cnb)

att=[asin(Cnb(3,2)); atan2(-Cnb(3,1),Cnb(3,3)); atan2(-Cnb(1,2),Cnb(2,2))];
    
return

从方向余弦到欧拉角（此程序没有考虑奇异点、但是在严老师的PSINS中考虑了）

 INS_4——earth_update.m

function eth=earth_update(pos,vel)
eth.Re = 6378137;                    
eth.f  = 1/298.257223563;            
eth.Rp = (1-eth.f)*eth.Re;           
eth.e1 = sqrt(eth.Re^2-eth.Rp^2)/eth.Re;
eth.e2 = sqrt(eth.Re^2-eth.Rp^2)/eth.Rp; 
eth.wie = 7.2921151467e-5;           
eth.g0 = 9.7803267714;   

以上是WGS84椭球参数

1、长半轴a = 6378137.0 m、短半轴b=6356752.3142m、扁率f =1/298.257223563;长半轴a = 6378137.0 m、短半轴b=6356752.3142m、扁率f =1/298.257223563、第─偏心率平方(e2)= 0.00669437999013、第二偏心率平方(e 2)= 0.00673949674222。

2、地球自转角速度= 7.292115×10-5 rad/s、椭球正常重力位= 62636860.8497 m2/s2、赤道正常重力=9.7803267714m/s2。

B = pos(1); L = pos(2); h = pos(3); 
ve = vel(1); vn = vel(2); vu = vel(3); 
eth.RN = eth.Re/sqrt(1-eth.e1^2*sin(B)^2);           
eth.RM = eth.RN*(1-eth.e1^2)/(1-eth.e1^2*sin(B)^2); 
eth.Mpv2 = sec(B)/(eth.RN+h);
eth.Mpv4 = 1/(eth.RM+h);
eth.RNh  = eth.RN+h;
eth.RMh  = eth.RM+h;
eth.tanL = tan(B);
eth.secL = sec(B);
eth.sinL = sin(B);
eth.cosL = cos(B);
eth.sin2L= sin(2*B);
eth.cos2L= cos(2*B);

1、B、L、H代表地理坐标的纬度、经度和大地高 

2、ve 东向速度、vn北向速度、vu天向速度

3、ethRN、ethRM代表子午圈曲率半径和卵酉圏曲率半径

% earth rotation rate projected in the n-frame
eth.wnie = [0; eth.wie*cos(B); eth.wie*sin(B)];

% the rate of n-frame respect to e-fame projected in the n-frame
eth.wnen = [-vn/(eth.RM+h); ve/(eth.RN+h); ve/(eth.RN+h)*tan(B)];

% the rate of n-frame respect to i-fame projected in the n-frame
eth.wnin = eth.wnie + eth.wnen;

% earth gravity vector projected in the n-frame
eth.g  = eth.g0*(1+5.27094e-3*sin(B)^2+2.32718e-5*sin(B)^4)-3.086e-6*h; 
eth.gn = [0; 0; -eth.g];

% gcc:gravitational acceleration/coriolis acceleration/centripetal acceleration
eth.wnien = 2*eth.wnie + eth.wnen;
eth.gcc = -cross(eth.wnien,vel)+eth.gn;

return

1、e系相对于i系的旋转角速度在n系下的投影

2、n系相对于e系的旋转角速度在n系下的投影

3、n系相对于i系的旋转角速度在n系下的投影

4、在n系下计算重力（重力模型方法有很多只是ginav中是这一种方法）

 5、哥氏加速度有害加速度

 只有在加速度计输出中扣除有害加速度后，才能获得运载体在导航系下的几何运动加速度

INS_5——rvecmat.m

function mat=rvec2mat(vec)
% convert rotation vector to transformation matrix

theta=sqrt(vec'*vec);
mat=eye(3)+(sin(theta)/theta*askew(vec))+...
     ((1-cos(theta))/theta^2*(askew(vec))^2);

return

旋转矢量转方向余弦

 theat为等效旋转矢量其矢量方向表示为转轴方向，而模的大小表示为旋转角度大小

INS_6——update_trans_mat.m

更新状态转移矩阵

function Phi=update_trans_mat(ins)

zero33 = zeros(3);
tanL = ins.eth.tanL;   secL = ins.eth.secL;
sin2L= ins.eth.sin2L;  cos2L= ins.eth.cos2L;
RNh  = ins.eth.RNh;    RMh  = ins.eth.RMh;
vE   = ins.vel(1);     vN   = ins.vel(2);  vU   = ins.vel(3); %#ok

F1=zero33; F1(2)=-ins.eth.wnie(3); F1(3)=ins.eth.wnie(2);

F2=zero33; F2(2)=1/RNh; F2(3)=tanL/RNh; F2(4)=-1/RMh;

F3=zero33; F3(3)=vE*secL^2/RNh; F3(7)=vN/RMh^2; F3(8)=-vE/RNh^2; F3(9)=-vE*tanL/RNh^2;

x = -ins.eth.g0*sin2L*(5.27094e-3-4*2.32718e-5*cos2L); 
F4=zero33; F4(3)=x; F4(9)=3.086e-6;

1、先生成3*3的0矩阵，共有四个0矩阵F1、F2、F3，F4往里面赋值

2、F1与e系相对于i系的旋转角速度在n系下的投影有关

3、F2与子午圈曲率半径和卵酉圏曲率半径有关

4、F3与东向速度北向速度、子午圈曲率半径、卵酉圏曲率半径有关

 5、F4与g、相关

​
% transition matrix for phi
Faa = -askew(ins.eth.wnin);     
Fav = F2;
Fap = F1+F3;

​

% transition matrix for delta-vel
Fva = askew(ins.fn);
Fvv = askew(ins.vel)*F2 - askew(ins.eth.wnien);
Fvp = askew(ins.vel)*(2*F1+F3+F4);

 

% transition matrix for delta-pos
Fpp = zero33; Fpp(2)=vE*secL*tanL/RNh; Fpp(7)=-vN/RMh^2; Fpp(8)= -vE*secL/RNh^2;
Fpv = ins.Mpv;    

% time continuous state transition matrix
Ft = [ Faa       Fav       Fap      -ins.Cnb            zero33
       Fva       Fvv       Fvp      zero33              ins.Cnb
       zero33    Fpv       Fpp      zero33              zero33
       zero33    zero33    zero33   diag(-1./ins.tauG)  zero33
       zero33    zero33    zero33   zero33              diag(-1./ins.tauA)];      

 

% discretization
if ins.nt>0.1
    Phi = expm(Ft*ins.nt); 
else
    Phi = eye(size(Ft))+Ft*ins.nt;
end

return

 当ins.nt大于0,1时，Phi以（Ft*ins,nt）求矩阵的以e为底数的指数函数,否则就是单位阵加上Ft*int,nt

 

 

INS_7——ins_init.m

function ins=ins_init(opt,avp0)
% sample date
ins.nt = 1/opt.sample_rate;
ins.old_imud = zeros(1,6);

惯导初始化——采样时间

ins.old_imud一行六列的零矩阵

 

% initialize position,attitude and velocity
ins.att = avp0(1:3);
ins.vel = avp0(4:6);
ins.pos = avp0(7:9);
ins.acc = zeros(3,1);
ins.Cnb = att2Cnb(ins.att);

惯导初始化——位置、姿态和速度

% initialize imu error
ins.bg = zeros(3,1);
ins.ba = zeros(3,1);
ins.Kg = eye(3);
ins.Ka = eye(3);
ins.tauG = [inf;inf;inf];
ins.tauA = [inf;inf;inf];

% initialize earth related parameters
ins.eth = earth_update(ins.pos,ins.vel);
ins.Mpv = [0, ins.eth.Mpv4, 0; ins.eth.Mpv2, 0, 0; 0, 0, 1];
ins.wib = zeros(3,1);
ins.fb  = zeros(3,1);
ins.fn  = -ins.eth.gn;
ins.web = zeros(3,1);

初始化imu误差

% initialize earth related parameters
ins.eth = earth_update(ins.pos,ins.vel);
ins.Mpv = [0, ins.eth.Mpv4, 0; ins.eth.Mpv2, 0, 0; 0, 0, 1];
ins.wib = zeros(3,1);
ins.fb  = zeros(3,1);
ins.fn  = -ins.eth.gn;
ins.web = zeros(3,1);

初始化地球相关系数

% initialize state, state covariance matrix, system noise matrix
% state transition matrix, lever arm
init_att_unc = opt.init_att_unc;
init_vel_unc = opt.init_vel_unc;
init_pos_unc = opt.init_pos_unc;
init_bg_unc  = repmat(opt.init_bg_unc,1,3);
init_ba_unc  = repmat(opt.init_ba_unc,1,3);
psd_gyro = repmat(opt.psd_gyro,1,3);
psd_acce = repmat(opt.psd_acce,1,3);
psd_bg   = repmat(opt.psd_bg,1,3);
psd_ba   = repmat(opt.psd_ba,1,3);

ins.x  = [ins.att;ins.vel;ins.pos;ins.bg;ins.ba];
ins.P  = diag([init_att_unc,init_vel_unc,init_pos_unc,init_bg_unc,init_ba_unc].^2);
ins.Q  = diag([psd_gyro, psd_acce, zeros(1,3), psd_bg, psd_ba])*ins.nt;
ins.Phi= update_trans_mat(ins);
ins.lever = opt.lever';

ins.xa = zeros(15,1);
ins.Pa = zeros(15,15);

return

初始化状态、状态协方差矩阵、系统噪声矩阵、状态转换矩阵，杠杆误差

ins_8——ins_mech.m

function ins=ins_mech(ins,imu)
% INS mechanization
persistent old_dw old_dv

ins.time=imu.time;
if isempty(old_dw)
    old_dw=zeros(3,1); 
end
if isempty(old_dv)
    old_dv=zeros(3,1); 
end

1、定义持久变量old_dw、old_dv

2、判断old_dw、old_dv是否为空 

% correct bias and scaling factor errors
dw0 = imu.dw';
dv0 = imu.dv';
dw = ins.Kg*dw0-ins.bg*ins.nt;
dv = ins.Ka*dv0-ins.ba*ins.nt;

纠正零偏和比例因子误差

% extrapolate velocity and position
vel_mid = ins.vel+ins.acc*(ins.nt/2);                    
pos_mid = ins.pos+ins.Mpv*(ins.vel+vel_mid)/2*ins.nt; 

 

% update velocity 
dv_rot  = 0.5*cross(dw0,dv0);
dv_scul = 1/12*(cross(old_dw,dv0)+cross(old_dv,dw0));
dv_sf   = (eye(3)-0.5*ins.nt*askew(ins.eth.wnin))*ins.Cnb*dv + ins.Cnb*(dv_rot+dv_scul);
dv_cor  = ins.eth.gcc*ins.nt;
vel_new = ins.vel+dv_sf+dv_cor;

速度更新

这里采用的是双子样算法。但是与严老师的捷联惯导书中公式不同，这部分公式与牛老师的捷联惯导讲义对应，可以参考武大组合导航课程，牛老师详细介绍了其中的差别。

下面公式是严老师书中公式 

% update position 
ins.Mpv(2) = ins.eth.Mpv2;
ins.Mpv(4) = ins.eth.Mpv4;
pos_new    = ins.pos + ins.Mpv*(ins.vel+vel_new)/2*ins.nt; 

位置更新

 

% update attitude 
dw_cone  = 1/12*cross(old_dw,dw0);
phi_b_ib = dw+dw_cone;
phi_n_in = ins.eth.wnin*ins.nt;
Cbb = rvec2mat(phi_b_ib);
Cnn = rvec2mat(phi_n_in)';
Cnb_new = Cnn*ins.Cnb*Cbb;
att_new = Cnb2att(Cnb_new);

姿态更新

% update INS result
ins.Cnb = Cnb_new;
ins.att = att_new;
ins.vel = vel_new;
ins.pos = pos_new;
ins.x = [ins.att;ins.vel;ins.pos;ins.bg;ins.ba];

old_dw=dw0;
old_dv=dv0;

return

更新INS结果

INS_9——ins_time_update.m

function ins=ins_time_updata(ins)
% INS time update
ins.Phi=update_trans_mat(ins);

G=zeros(15,15);
G(1:3,1:3)=-ins.Cnb;
G(4:6,4:6)=ins.Cnb;
G(10:12,10:12)=eye(3);
G(13:15,13:15)=eye(3);

Q0=G*ins.Q*G';
P0=ins.P+0.5*Q0;
ins.P=ins.Phi*P0*ins.Phi'+0.5*Q0;

return

惯导时间更新

在一个滤波周期内，卡尔曼滤波的信息更新过程可以分为时间更新过程和量测更新过程。其中时间更新又被称为预测，一步预测的状态及其协方差阵为：

​​​​​​​