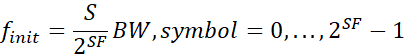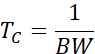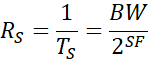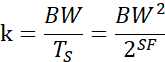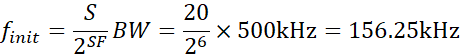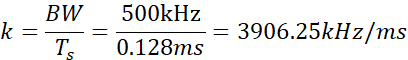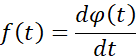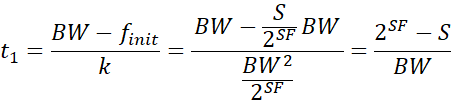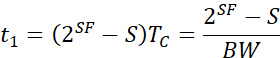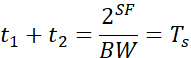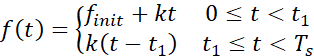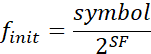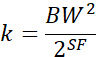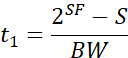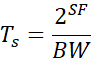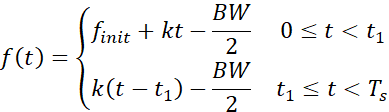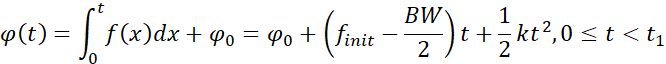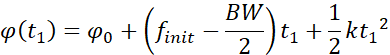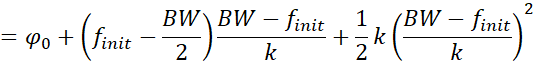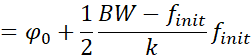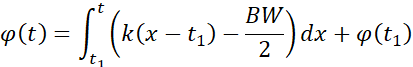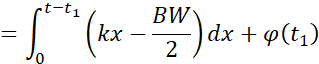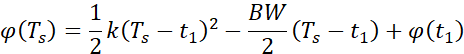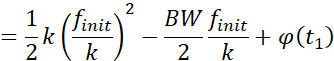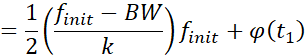LoRa PHY CSS调制分析及Matlab实现
目录
1. Chirp调制及关键指标
2. CSS调制及关键指标
2.1 扩频因子(SF: spreading factor)
2.2 码片率(chip rate)、符号率(symbol rate)和线性扫频斜率
3. CSS调制线性扫频
4. CSS调制基带实现
5. CSS调制Matlab实现示例
6. 参考Matlab代码
7. 参考文献
1. Chirp调制及关键指标
LoRa物理层采用CSS调制(Chirp Spread Spectrum)[1],实现公里级的无线信号传输距离,而CSS调制的核心是Chirp调制。
维基百科中的chirp定义[2]为:A chirp is a signal in which the frequency increases (up-chirp) or decreases (down-chirp) with time。因此,chirp本质上是一种在一定频率范围内扫频的信号。up-chirp指的是信号在频率定义的范围内不断增加,而down-chirp指的是信号在频率定义的范围内不断减小。
Chirp信号频率变化的方式来看,一般可以主要分为线性扫频(linear)、二阶扫频(quadratic)和指数扫频(logarithmic)三种。Matlab通过定义函数chirp产生不同扫描方式的扫频信号[3],其主要提供的扫描方式为:Linear,Quadratic,Logarithmic等。
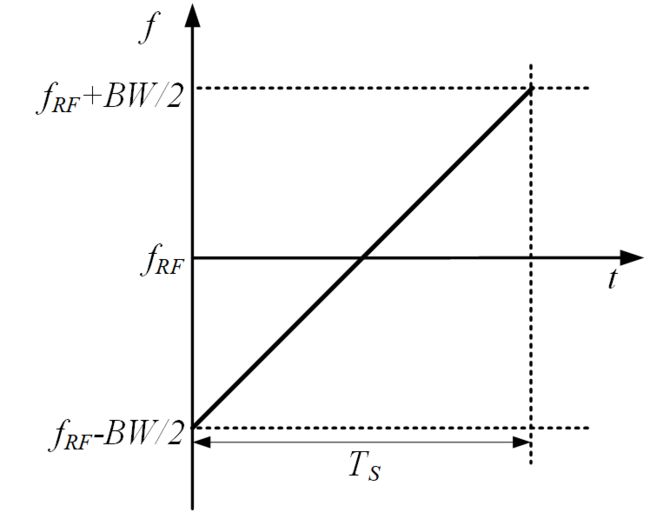
Lora通信中,chirp调制采用的是线性扫频,或也称为线性调频(LFM:linear frequency modulation)。图 1给出了一个频率线性扫描的chirp信号频率变化示意,由该示意中可以得到线性扫频chirp的关键参数:扫频起始频率,扫频终止频率,扫频带宽和扫频时间,线性扫频斜率。结合图 1示例,可以得到:
- 扫频起始频率:
![]()
- 扫频终止频率:
![]()
- 扫频带宽:
![]()
- 扫频时间:
![]()
- 扫频斜率:
![]()
其中![]() 为芯片收发的信道中心频率,例如433MHz等。
为芯片收发的信道中心频率,例如433MHz等。
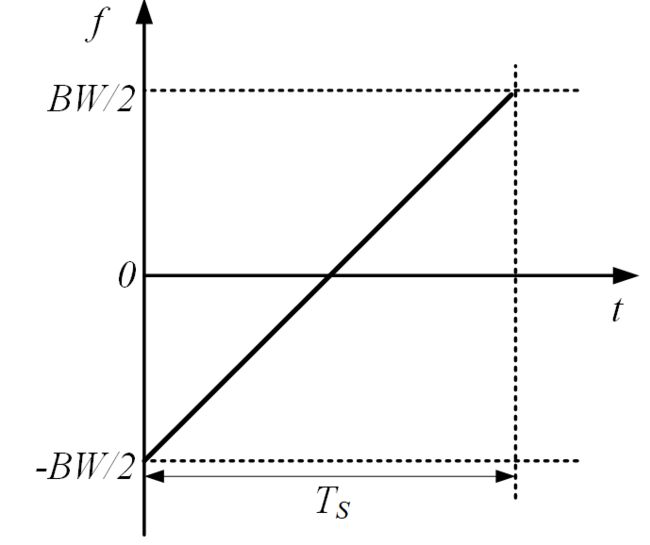
图 1给出的Chirp频率线性扫描是在射频信道中心频率表示的,但一般在基带处理时,不引入任何射频载波信号,此时Chirp信号在基带(信号中心频率为零)的频率线性扫描示意如图 2所示。如果在基带的Chirp用![]() 表示,那么将该信号转换至中心频率为
表示,那么将该信号转换至中心频率为![]() 的射频信号时,可以表示为:
的射频信号时,可以表示为:
![]()
实现频率变化的器件为射频发射机中的混频器和锁相环[4],其中混频器主要实现上式中的类似信号相乘功能,而锁相环主要提供频谱搬移所需要的射频载波频率。为了方便,后续都在基带讨论的CSS调制,也就是![]() 为0的情况。
为0的情况。
图 1 中心频率在![]() 的线性扫描Chirp信号频率随时间变化示意
的线性扫描Chirp信号频率随时间变化示意
图 2 基带中的线性扫描Chirp信号频率随时间变化示意
2. CSS调制及关键指标
上述chirp调制,不管是何种频率扫描方式,显然无法直接用来传递信息。因此LoRa采用了CSS技术,通过改变扫频的初始频率,来实现不同信息的传递。
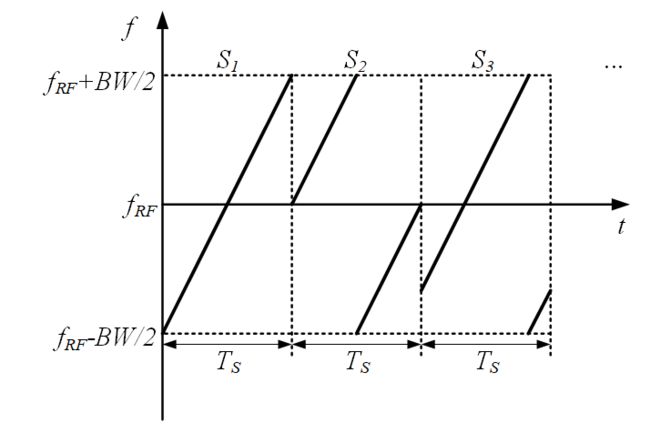
图 3给出了在RF端观察到的LoRa CSS调制频率线性扫描示例。该示例中给出了经过CSS调制后,传递三个符号(symbol)的频率线性扫描波形。由此可以看出LoRa的CSS调制,在每个符号传输时间TS内,调制信号的频率在整个带宽内实现了一次线性扫频变化。
由于改变扫描初始频率,因此在整个symbol传输时间内,频率线性递增会超过规定的扫描终止频率![]() 。此时CSS调制规定,一旦频率超过扫描频率上限,那么直接将后续的扫描频率减去BW,如图 3中的S2和S3所示。
。此时CSS调制规定,一旦频率超过扫描频率上限,那么直接将后续的扫描频率减去BW,如图 3中的S2和S3所示。
结合chirp调制时的参数,引入CSS调制后,额外定义了SF因子,码片率/符号率等参数。
图 3 RF端观察到的LoRa CSS调制频率线性扫描示意
2.1 扩频因子(SF: spreading factor)
为了明确无线传输中每个符号与传输bit数的关系,LoRa定义了扩频因子(SF: spreading factor),表示了每个符号中包含的信息比特数,也就是将每个符号扩频到![]() 码片上进行传输,同时也将不同的符号映射到了不同的CSS调制初始频率。
码片上进行传输,同时也将不同的符号映射到了不同的CSS调制初始频率。
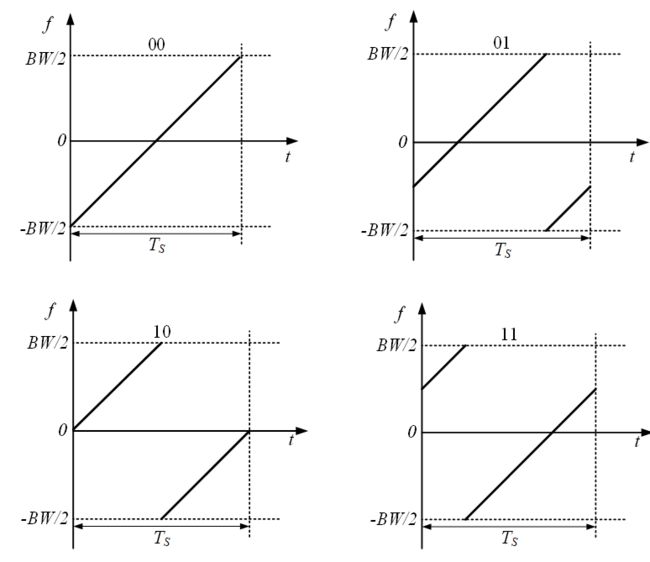
例如当SF为2时,每个符号由2个比特原始数据进行编码,此时每个符号有![]() 个码片。此时,如果在基带观察CSS调制,分别可以得到不同符号对应的初始频率,及频率线性递增后的调制波形,如图 4所示。由图 4可知,每个符号仍然在
个码片。此时,如果在基带观察CSS调制,分别可以得到不同符号对应的初始频率,及频率线性递增后的调制波形,如图 4所示。由图 4可知,每个符号仍然在![]() 时间内实现了整个带宽的频率线性扫描,但不同符号的扫描起始频率不同。对应上述例子,SF为2时,存在四种符号编码分别为00,01,10和11,对应CSS调制时的四种起始频率,分别为:
时间内实现了整个带宽的频率线性扫描,但不同符号的扫描起始频率不同。对应上述例子,SF为2时,存在四种符号编码分别为00,01,10和11,对应CSS调制时的四种起始频率,分别为:
如果需要传递符号编码为01的信息时,CSS调制传输起始频率分别为:[![]() ]的四个码片;而需要传递符号编码为10的信息时,CSS调制传输起始频率分别为[
]的四个码片;而需要传递符号编码为10的信息时,CSS调制传输起始频率分别为[![]() ] 的四个码片,并最终在规定时间内完成整个BW带宽内的频率线性扫描。
] 的四个码片,并最终在规定时间内完成整个BW带宽内的频率线性扫描。
更一般情况下,根据信号传输带宽和扩频因子,可以得到不同符号编码值S对应的频率初始值为:
因此如果能够解调出该符号的起始频率![]() ,再通过起始频率与符号的映射,就可以获得送入CSS调制器的无线传输比特数据。注意该比特数据与原始需要传输的信息之间还存在编解码的过程,因此通过解CSS调制获得的比特数据还不是原始需要传输的比特信息。
,再通过起始频率与符号的映射,就可以获得送入CSS调制器的无线传输比特数据。注意该比特数据与原始需要传输的信息之间还存在编解码的过程,因此通过解CSS调制获得的比特数据还不是原始需要传输的比特信息。
图 4 SF=2时四种编码对应的LFM调制基带频率波形
2.2 码片率(chip rate)、符号率(symbol rate)和线性扫频斜率
LoRa在芯片及应用说明[1]中,定义了码片率,即:“one chip is sent per second per Hz of bandwidth”,因此我们可以得到每个码片的传输速率,即码片率为:
![]()
其中,BW是CSS调制所使用的带宽。因此,我们可以得到每个码片的传输时间:
而定义扩频因子SF之后的每个CSS符号包含![]() 个码片,因此符号的传输时间可以表示为:
个码片,因此符号的传输时间可以表示为:
同样,进一步可以得到CSS调制后的符号率为:
根据CSS调制指定的传输带宽和SF之后,进一步我们可以计算获得chirp调制中频率线性增加的斜率为:
3. CSS调制线性扫频
如果已知频率初始值![]() 及频率线性递增的斜率,那么我们可以得到线性频率递增的表达式为:
及频率线性递增的斜率,那么我们可以得到线性频率递增的表达式为:
![]()
其中,![]() 为CSS调制的初始扫描频率,
为CSS调制的初始扫描频率,![]() 为CSS调制频率线性递增的斜率,
为CSS调制频率线性递增的斜率,![]() 为每个符号的传输时间。
为每个符号的传输时间。
显然,上述描述当![]() 不为0时,
不为0时,![]() 完成整个调制时间0~
完成整个调制时间0~![]() 的扫频后,在有段时间范围内,
的扫频后,在有段时间范围内,![]() 超过了BW,因此需要Mod处理,即:
超过了BW,因此需要Mod处理,即:
![]()
上述CSS调制频率随时间的描述,是信号在0~BW范围内的表示形式,显然此时信号的中心频率在![]() 。因此如果考虑基带时的波形频率描述方式,那么可以最终得到中心频率为0时候的CSS调制频率表达式:
。因此如果考虑基带时的波形频率描述方式,那么可以最终得到中心频率为0时候的CSS调制频率表达式:
下面三幅图分别展示了![]() ,
, ![]() ,
, ![]() (对应SF为6时的二进制数为:010100b)。根据上述定义,CSS信号频率初始值为:
(对应SF为6时的二进制数为:010100b)。根据上述定义,CSS信号频率初始值为:
每个符号所需要的时间为:
信号递增的斜率为:
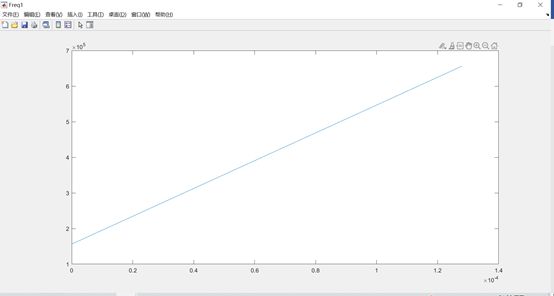
如图 5所示,该信号如果以![]() 作为起始频率开始以
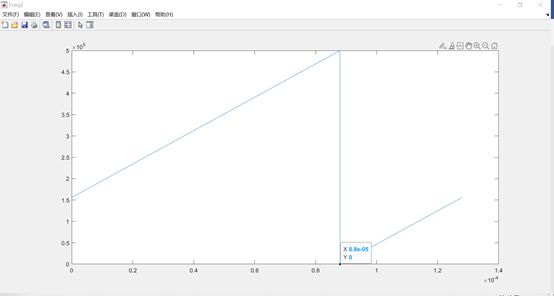
作为起始频率开始以![]() 线性递增,那么在0.088ms处频率将超过500kHz,因此,后续扫描频率将减去500kHz后,继续开始扫描,如图 6所示。最终将整体扫频信号扣除250kHz后,得到最终的基带信号,如图 7所示。
线性递增,那么在0.088ms处频率将超过500kHz,因此,后续扫描频率将减去500kHz后,继续开始扫描,如图 6所示。最终将整体扫频信号扣除250kHz后,得到最终的基带信号,如图 7所示。
图 5 初始频率开始的频率线性扫描
图 6 扫描频率限制在0~BW带宽内
图 7 基带无载波情况下的扫描频率
4. CSS调制基带实现
得到带有符号的扫频信号![]() 后,需要得到频率按照要求变换的正弦信号,由于相位和频率之间满足积分关系,因此
后,需要得到频率按照要求变换的正弦信号,由于相位和频率之间满足积分关系,因此![]() 信号对应的相位值为:
信号对应的相位值为:
其中![]() 为相位的初始值(如果存在的话)。显然,存在:
为相位的初始值(如果存在的话)。显然,存在:
那么最终得到调制后的信号为:
![]()
如果用IQ发射机进行上变频,那么基带IQ信号可以表示为:
最终,经过IQ发射机上变频至射频信道的最终信号为:
![]()
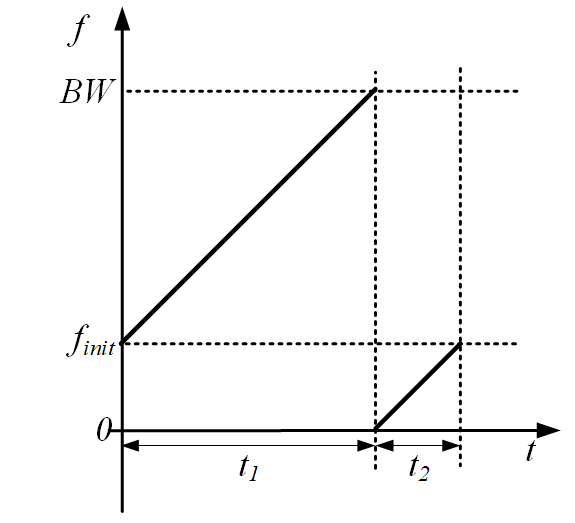
因此,重点需要得到不同符号S,带宽BW和SF对应下的![]() 表达式。为了便于描述,我们首先在0~BW带宽上进行描述,如图 8。
表达式。为了便于描述,我们首先在0~BW带宽上进行描述,如图 8。
图 8 LoRa CSS线性扫频分段描述
根据CSS调制定义,整个符号的传输时间划分了了![]() 份,每份用来传输一个码片。如果将整个扫频过程中的频率是否超过BW,可以得到两段不连续的线性扫频频率。其中第一段波形频率由
份,每份用来传输一个码片。如果将整个扫频过程中的频率是否超过BW,可以得到两段不连续的线性扫频频率。其中第一段波形频率由![]() 开始扫描,并结束至BW,因此可以得到第一段的持续时间为:
开始扫描,并结束至BW,因此可以得到第一段的持续时间为:
也就是码片符号由S递增至![]() ,共遍历了
,共遍历了![]() 个码片,而每个码片持续时间为
个码片,而每个码片持续时间为![]() ,因此
,因此![]() 也可以写成:
也可以写成:
对比发现,两者的最终表达形式是一致的。
而第二段频率是从0线性递增至![]() ,也可以理解为码片符号由0递增至S-1所需要的时间,同样可以得到:
,也可以理解为码片符号由0递增至S-1所需要的时间,同样可以得到:
显然,我们可以得到:
因此,第一段频率线性扫描后得到的频率表达式为:
![]()
而第二段频率线性扫描后得到的频率表达式为:
![]()
综上,可以得到:
其中:
将上述扫频信号去除中心频率,得到基带扫频信号频率为:
由于相位是频率函数的积分,因此在第一段时间内的相位变化可以表示为:
其中,![]() 是CSS调制的起始相位。基带发射情况下,可以令
是CSS调制的起始相位。基带发射情况下,可以令![]() 。而第一段CSS调制结束时,即时间到达
。而第一段CSS调制结束时,即时间到达![]() 时刻相位为:
时刻相位为:
而在第二段时间内的相位变化可以表示为:
其中,![]() 。那么第二段时间CSS调制结束时,即时间到达
。那么第二段时间CSS调制结束时,即时间到达![]() 时刻相位为:
时刻相位为:
![]()
也就是第二段调制后的相位,从![]() 又变化回了
又变化回了![]() 。也就是说,Lora采用的CSS调制,在整个symbol符号内,属于连续相位调制。
。也就是说,Lora采用的CSS调制,在整个symbol符号内,属于连续相位调制。
5. CSS调制Matlab实现示例
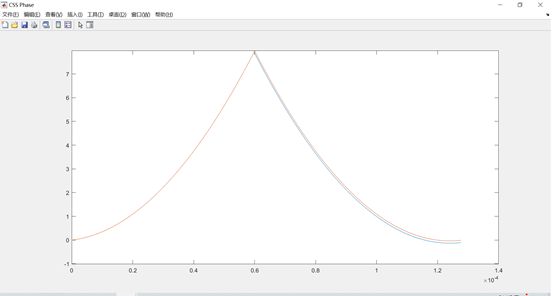
根据上述分析,下面分别给出了两种实现LoRa CSS 单个符号调制的Matlab代码。其中第一种代码直接利用matlab提供的cumtrapz函数[5]实现频率点的积分(图 9中蓝色曲线),而第二种方法直接采用上述分段相位积分公式推导后采样得到(图 9中红色曲线)。通过对比,可以发现两者在到达频率最大值后存在不一致。同时通过窗口打印两种方法![]() 点的相位,可以发现第一种方法存在误差。
点的相位,可以发现第一种方法存在误差。
进一步分析可以得到,该误差是Matlab函数cumtrapz算频率积分求相位产生的,具体此处不在展开。
图 9 两种方法产生的相位积分
图 10 由相位生成LoRa CSS IQ波形
6. 参考Matlab代码
close all; clear all; clc;
BW=500e3; %CSS调制带宽
SF=6; %CSS调制SF因子
samp_per_code=5; %CSS调制每个扩频code时间段内的采样点数
symbol_value=34; %当前待调试的符号值
N=2^SF; %code 总数
T_symbol=N/BW %symbol占用时间
SampleRate=samp_per_code*BW; %实际采样率
Npts=samp_per_code*N; %总采样点数
t=(0:Npts)/SampleRate; %CSS调制抽样时刻,需要的采样时刻序号应该为0:Npts-1,最后一个用于验证相位连续性
init_freq=symbol_value/N*BW; %初始频率
k=BW/T_symbol; %频率增加斜率
%%Lora CSS 调制方法1
freq1=init_freq+k*t; %根据初始频率生成线性扫频
freq2=mod(freq1,BW); %将freq1限制在0~BW带宽内
freq3=freq2-BW/2; %将freq2中心频率设置为0
tmp=cumtrapz(t,freq3); %使用累计梯形数值积分函数,进行相位积分
phase_final1=tmp(end) %最后一个点用于观察相位连续性
Theta_Method1=tmp(1:end-1); %删除最后一个点
%%Lora CSS 调制方法2
Npts1=samp_per_code*(N-symbol_value); %t1时间段对应总采样点数
t1=(0:Npts1)/SampleRate; %t1时间段实际相位采样时刻,需要的采样时刻序号应该为0:Npts1-1,最后一个点为第二段的起始相位
tmp=(init_freq-BW/2)*t1+1/2*k*t1.*t1; %根据第一段相位公式计算
Theta1=tmp(1:end-1); %第一段相位取值
Theta_init=tmp(end); %第一段相位在t1时刻的取值
t2=(Npts1:Npts)/SampleRate; %第二段相位采样时刻
t2=t2-t1(end);
tmp=1/2*k*t2.*t2-BW/2*t2+Theta_init; %根据第二段相位公式计算
phase_final2=tmp(end)
Theta_Method2=[Theta1 tmp(1:end-1)];
figure('Name', 'CSS Phase','NumberTitle', 'off');
plot(t(1:end-1),Theta_Method1)
hold on
plot(t(1:end-1),Theta_Method2)
hold off
s=exp(j*2*pi*Theta_Method2);
figure('Name', 'waveform','NumberTitle', 'off');
plot(real(s))
hold on
plot(imag(s))
hold off7. 参考文献
[1] Semtech Corporation, AN1200.22 LoRa Modulation Basics, 2015
Salesforce
[2] https://en.wikipedia.org/wiki/Chirp
[3] Swept-frequency cosine - MATLAB chirp- MathWorks 中国
[4] 东南大学,射频通信电路:射频收发机结构,第四讲 射频收发机结构 - 豆丁网
[5] Matlab, 累积梯形数值积分 - MATLAB cumtrapz- MathWorks 中国