其他算法-非线性降维t-SNE

t-SNE

流形学习

流形（manifold）是几何中的一个概念，它是高维空间中的几何结构，即空间中的点构成的集合。可以简单的将流形理解成二维空间的曲线，三维空间的曲面以及在更高维空间的推广；

流形学习，全称流形学习方法(Manifold Learning)，流形学习就是从高维采样数据中恢复低维流形结构，即找到高维空间中的低维流形，并求出相应的嵌入映射，以实现维数约简或者数据可视化。它是从观测到的现象中去寻找事物的本质，找到产生数据的内在规律；

比如下图的三维数据，可以降维至二维，去除数据的冗余：

SNE算法原理

对于一个包含大量特征的数据集，降维是探索数据内隐藏模式的一种方式，虽然SVD和PCA可以降维（回顾：SVD奇异值分解和PCA主成分分析），但它们属于线性降维；不能合理地处理特征之间的复杂非线性关系；因此，出现了非线性降维算法SNE（stochastic neighbor embedding）；

假设输入的高维空间变量为$X\in {\mathbb{R}}^n$，输出低维空间变量为$Y\in {\mathbb{R}}^t$，其中$t\ll n$，假设样本数量为$m$，则输入到输出为$(x_1,...,x_m),x\in X,(y_1,...,y_m),y\in Y$；

SNE先计算高维空间中，样本间的相似度，用条件概率表示，比如对于样本$x_i$，计算$x_i$和$x_j$的相似度$p_{j|i}$：
$$p_{j|i}=\frac{exp(-\frac{||x_i-x_j|{|}^2}{2{\sigma }_i^2})}{{\sum }_{k\ne i}exp(-\frac{||x_i-x_k|{|}^2}{2{\sigma }_i^2})}$$
高维空间引入参数${\sigma }_i$与每个样本$x_i$对应，增加泛化能力，另外，目标是刻画不同样本之间的相似度，所以设置同一个样本的相似度为$p_{i|i}=0$，使之不参与计算；

对于低维空间，进行类似的表达，对于样本$y_i$，$y_i$和$y_j$的相似度$q_{j|i}$为：
$$q_{j|i}=\frac{exp(-||y_i-y_j|{|}^2)}{{\sum }_{k\ne i}exp(-||y_i-y_k|{|}^2)}$$
同样的，$q_{i|i}=0$；

降维的目的是在减少特征维度的同时，保持数据分布的相似，即希望$p_{j|i}=q_{j|i}$，KL散度可以衡量两个分布的相似程度（分布越相似，KL散度越小），因此损失函数定义为两个分布的KL散度：
$$L=\sum _{i}KL(P_i||Q_i)=\sum _i(\sum _j{p}_{j|i}log(\frac{p_{j|i}}{q_{j|i}}))$$
其中，$P_i$表示给定高维样本$x_i$后，它与其他高维样本的相似度分布；$Q_i$表示给定低维样本$y_i$后，它与其他低维样本的相似度分布；

SNE的目标就是找到合适的分布$Q_i$，$i\in \left\{1,2,...,m\right\}$，使损失变小，即：使得降维前后的数据分布相似；

SNE求解

对于每个样本$x_i$，都对应着不同的${\sigma }_i$，SNE引入困惑度，困惑度是人为取值，根据困惑度计算${\sigma }_i$，困惑度定义为：
$$Perp(P_i)=2^{H(P_i)}$$
其中，$H(P_i)$为信息熵（信息熵回顾：图神经网络第六课-GNN的可解释性），困惑度的调整体现了泛化能力，通常取值在5到50之间，给定困惑度后可以计算得到${\sigma }_i$；

随后，计算损失函数关于$y_i$的梯度，基于梯度下降更新$y_i$，一般会采用结合动量的梯度下降进行更新；

对称SNE

对称SNE意图使用联合概率分布替换条件概率分布，近似地，得到表达：
$$p_{ij}=\frac{p_{i|j}+p_{j|i}}{2},q_{ij}=\frac{exp(-||y_i-y_j|{|}^2)}{{\sum }_{k\ne l}exp(-||y_k-y_l|{|}^2)}$$
此时概率具有对称性：$p_{ij}=p_{ji}$，$q_{ij}=q_{ji}$，损失函数变为：
$$L=\sum _{i}KL(P_i||Q_i)=\sum _i(\sum _j{p}_{ij}log(\frac{p_{ij}}{q_{ij}}))$$

t-SNE

t-SNE（t-distributed stochastic neighbor embedding）在对称SNE的基础上，将低维空间的高斯分布变成$t$分布，得到：
$$q_{ij}=\frac{(1+||y_i-y_j|{|}^2{)}^{-1}}{{\sum }_{k\ne l}(1+||y_k-y_l|{|}^2{)}^{-1}}$$
高维空间的分布不发生变化：
$$p_{j|i}=\frac{exp(-\frac{||x_i-x_j|{|}^2}{2{\sigma }_i^2})}{{\sum }_{k\ne i}exp(-\frac{||x_i-x_k|{|}^2}{2{\sigma }_i^2})},p_{ij}=\frac{p_{i|j}+p_{j|i}}{2m}$$
损失函数还是：
$$L=\sum _{i}KL(P_i||Q_i)=\sum _i(\sum _j{p}_{ij}log(\frac{p_{ij}}{q_{ij}}))$$
对于高维数据$X$，t-SNE算法流程为：

• 给定困惑度，计算得到${\sigma }_i$，然后计算$p_{j|i}$；
• 计算$p_{ij}=\frac{p_{i|j}+p_{j|i}}{2m}$，使用正态分布$N(0,10^{-4})$初始化低维空间$Y$；
• 迭代$T$次，每次迭代内容为：根据低维空间$Y$计算$q_{ij}$，计算损失$L$，计算梯度$\frac{\partial L}{\partial y_i}$，结合动量的梯度下降更新$y_i$；

基于sklearn的t-SNE

在sklearn中已经提供了t-SNE工具，可以方便地使用t-SNE对数据进行非线性降维，实例如下：

%matplotlib inline
from sklearn.manifold import TSNE
from sklearn.datasets import load_digits
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
import numpy as np

#在默认设置的matplotlib中图片分辨率不是很高，可以通过设置矢量图的方式来提高图片显示质量
%config InlineBackend.figure_format = "svg"

# 加载数据集
digits = load_digits()
print(digits.target,len(digits.target))

# t-SNE降维
X_tsne = TSNE(n_components=2, random_state=33).fit_transform(digits.data)
# PCA降维
X_pca = PCA(n_components=2).fit_transform(digits.data)

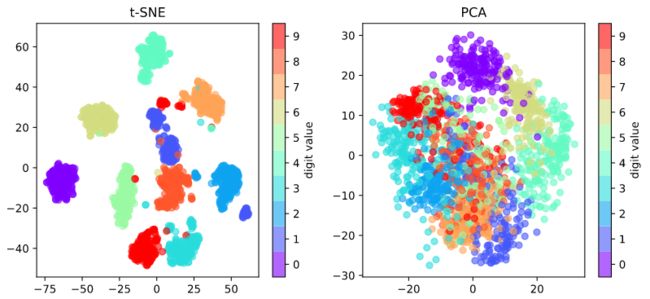
对结果进行可视化：

plt.figure(figsize=(8.5, 4))
# t-SNE降维结果可视化
plt.subplot(1, 2, 1) 
plt.scatter(X_tsne[:, 0], X_tsne[:, 1], c=digits.target, alpha=0.6, 
            cmap=plt.cm.get_cmap('rainbow', 10)) # 设置颜色和标签的映射,与关键字参数c对应
plt.title("t-SNE")
cbar = plt.colorbar(ticks=range(10)) 
cbar.set_label(label='digit value')
plt.clim(-0.5, 9.5) # 设置颜色条的范围

# PCA降维结果可视化
plt.subplot(1, 2, 2)
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=digits.target, alpha=0.6, 
            cmap=plt.cm.get_cmap('rainbow', 10)) # 设置颜色和标签的映射,与关键字参数c对应
plt.title("PCA")
cbar = plt.colorbar(ticks=range(10)) 
cbar.set_label(label='digit value')
plt.clim(-0.5, 9.5) # 设置颜色条的范围

plt.tight_layout() # 自动调整子图参数，使之填充整个图像区域
plt.show()

可以看出，使用非线性降维的结果明显优于线性降维