【SFS线性化方法】Tsai方法在侧扫声呐中的应用(一)
1、SFS简介与朗伯模型
SFS(Shape From Shading),即明暗还原形状,是一种根据图像灰度强弱预测并恢复物体形状的方法。
经典的SFS分为最小化法、局部分析法、演化法和线性化法。其中线性化法代表有Horn、Pentland和Tsai方法等,国内有赵建虎的补充等等。
SFS大多都依赖一个基本的原则:即兰伯特(Lambertian)反射模型(又称朗伯模型)。即反射体向各个方向反射强度相同,都与入射光和入射点表面法线之间的夹角的余弦值成正比。
即
E ∝ c o s < e ⃗ , e s ⃗ > E∝cos<\vec{e},\vec{e_s}> E∝cos<e,es> (1)
其中,E是反射强度(散射强度,各个方向强度大小相同), e s ⃗ \vec{e_s} es是入射波的方向向量, e ⃗ \vec{e} e是物体表面的法向量。当我们将反射强度进行归一化后,即按照灰度进行映射至[0,1]内的归一化后,就可以把正比号改为等号。我们不妨令
e s ⃗ = ( p s , q s , − 1 ) ; e ⃗ = ( p , q , − 1 ) \vec{e_s}=(p_s,q_s,-1);\vec{e}=(p,q,-1) es=(ps,qs,−1);e=(p,q,−1);
当然,这里没有进行约束,即两向量夹角可能出现余弦值为负数的情况,而这种情况实际上代表着某一面处在阴影中无法被照射到,我们先不予考虑。
把上述具体的 e ⃗ \vec{e} e和 e s ⃗ \vec{e_s} es带入到(1)式中,便可到得,
E ( x , y ) = R ( p , q ) = p p s + q q s + 1 1 + p s 2 + q s 2 1 + p 2 + q 2 E(x,y)=R(p,q)=\frac{pp_s+qq_s+1}{\sqrt{1+{p_s}^2+{q_s}^2}\sqrt{1+p^2+q^2}} E(x,y)=R(p,q)=1+ps2+qs21+p2+q2pps+qqs+1 (2)
2、SSS原理介绍与SFS应用
SSS(Side Scan Sonar),即侧扫声呐,是一种用于海洋勘测的常见仪器。由于海洋内电磁波谱吸收率高,且视觉传导容易受到浑浊海水和鱼群干扰,声呐在海洋勘测中使用广泛。侧扫声呐的示意图如下
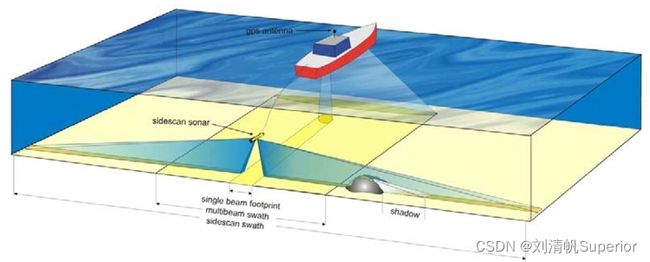 图 1 图1 图1
图 1 图1 图1
侧扫声呐固定在拖鱼上,通过电缆和船舶相连,它具有两个展开角度,其中一个是图上的显示的方向,此方向上的单侧展开角度可达数十度,而另一个展开角度展开方向与船舶航行方向平行,此方向上的展开角度只有零点几度,可以对其进行忽略。
侧扫声呐的主要原理就是,在船舶拉着拖鱼航行的每一个瞬间,向左右两侧的每个主要展开角度发射一次声波,声波遇到水体或者障碍物会反射,这种反射我们可以理想化为朗伯反射,声波会根据障碍物的远近一次返回(离海底越近返回的越早),并将其按照返回的早晚顺序记录下来,构成了一Ping的数据,如下图
 图 2 图2 图2
图 2 图2 图2
从左至右,表示声波返回的早晚,而高低表示的是声波的强度。返回声波强度是不一致的这是显然的。比如我们假设某一处海床到声呐拖鱼的距离不变,因此其回波时间是一定的,即在上图横坐标位置是确定的。而它的微观形状可以发生改变,导致了朗伯反射中的夹角发生了变化,这就导致同一处横坐标下,其强度(纵坐标)是可以改变的。
我们将每一瞬间拖鱼发出一Ping受到的如上图的信号,按照航行方向进行拼接,然后根据其信号强弱对其上色,如灰度或者金黑,便有了下图这样的侧扫声呐原始图像
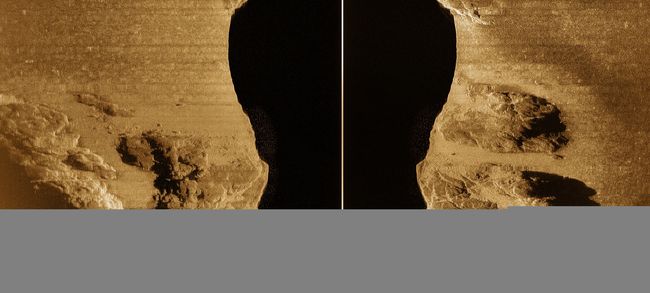 图 3 图3 图3
图 3 图3 图3
这样的原始数据一般都是每一Ping进行拼接,并附上文件头,形成一份XTF文件。一般需要用特别的软件进行解码打开,也可以自己根据XTF文件格式编写程序进行解码。这里使用的软件是DeepView,该公司官网可以提供免费版本的软件,美中不足的是无法进行图像直接导出,直接截图则会导致分辨率下降影响地形重建精度。
该软件实际上还提供了一些简易的工具,例如测量某处的高度,测量距离等等,其实测量高度实际上已经完成了简单的地形重建。下面我们根据原理来分析一下如何获得拖鱼距离海底高度 H H H
首先,根据图2和图3都可以看出,靠近拖鱼的地方是黑的(信号很微弱),此处一般被称为水柱区,因为信号从发出到接收之间肯定存在着传播时间,因此不可能有信号在很短的时间内直接返回,直接返回的是声波在水体中反射回来被接收的微弱信号,因为非常微弱,所以在图2里靠近左侧的一部分信号非常微弱,图三中靠近中间一部分是黑色。
而在图二中,我们观察到从最左侧往右,会有一段信号强度突然升高的部分,然后信号强度从左至右总体上呈现出下降态势。这是因为声波在水体中传播不同于光波在电磁波中传播,声波会被水体吸收,而这种吸收显然与声波传播路径有关,传播路径越长,声波被水体吸收的能量越多;传播路径越短,声波被水体吸收的能量越少。因此,出去水柱区微弱信号,到达海床的声波,返回的越早,就说明该方向上路径越短,因此信号被水体吸收的越少,就相对较强。因此在此种情况下,我们若要研究海底地形,就要排除水体吸收的影响,进行增益补偿,这种方法在刘小菊的文章中提到。除此之外,由于侧扫声呐原始图像横向表示的是两侧声波返回的先后顺序,实际上与海底某处到拖鱼声呐的直线距离(即斜距 S D SD SD成正比),而表现在侧扫声呐原始图像上的却是水平距离(平距 P D PD PD),因此需要对其进行斜距校正。
P D = S D 2 − H 2 PD=\sqrt{SD^2-H^2} PD=SD2−H2 (3)
这里因为地形是微观要素,而距离是宏观要素,所以我们对两者进行解耦,先斜距校正,再通过朗伯反射还原地形(即在 S D > > △ H SD>>△H SD>>△H的条件下)。将拖鱼与海底某处的高度差近似认为是等于拖鱼到当地形相对于距离不可忽略时,又应该使用别的办法,这是大多基于SFS的SSS三位重建论文没有考虑的
在进行了增益补偿、斜距校正后,实际上还需要进行地理坐标转换,也被称作拼贴(mosaic),但是在本研究中,我们仅仅研究简单的短距离小范围重建,而非大范围重建,因此这里地理坐标转换我们先不考虑。
至此,从声呐获得的XTF原始文件就被我们预处理完毕了,接下来可以用此图来进行基于SFS原理的海底侧扫声呐三维重建工作了。不过,我们还需要介绍一下,如何获取每一Ping的 H H H,即拖鱼声呐距离海底的直线高度。
勘测船舶一般会同时带上单波束声呐进行联合测量,这时从单波束声呐可以直接获得拖鱼距离海底的高度 H H H,见图1所示。具体方法是从每Ping的注脚上直接进行解码获取。(参考邓雪清等人)
3、应用SFS技术实现SSS海底三维地形重建
如前所述,SFS技术内涵广泛,我们研究的是线性化方法中的Tsai方法。其方法主要由公式(2)借助泰勒展开推导而来,具体详见论文,这里详细介绍的是Tsai方法在侧扫声呐情景下的变形推导。
首先,我们对每一Ping建立拖鱼声呐坐标系如下两张图
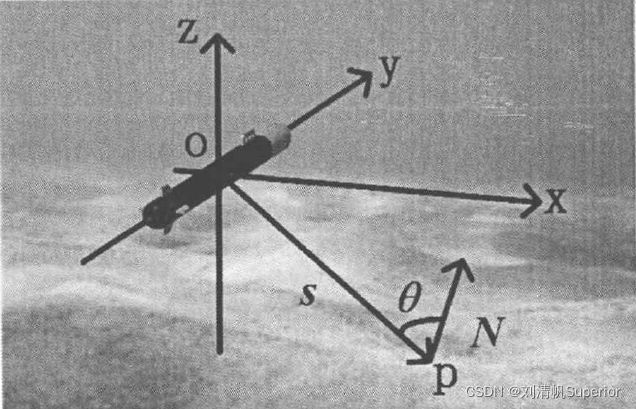
图 4 图4 图4
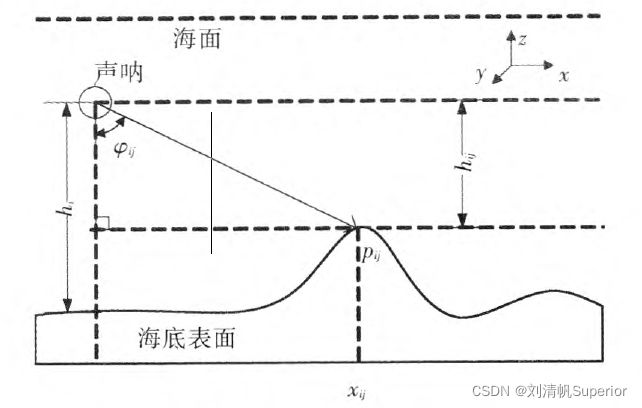
图 5 图5 图5
根据上图坐标系可以发现,这样建立坐标系保证了声波入射方向向量 e ⃗ \vec{e} e和海底法向量 e s ⃗ \vec{e_s} es夹角小于90°(其第三个分量都是-1,并且都控制在声呐的一侧)
以拖鱼前进平行方向为y方向,以侧扫声呐两侧方向为x方向,以指向海面方向为z方向建立坐标系。我们容易得到声波入射方向向量 e ⃗ \vec{e} e和海底法向量 e s ⃗ \vec{e_s} es的表达。
e s ⃗ = ( x i j h i j , 0 , − 1 ) ( 4 ) \vec{e_s}=(\frac{x_{ij}}{h_{ij}},0,-1) \qquad\qquad(4) es=(hijxij,0,−1)(4)
其中,由于(i,j)坐标处的Z坐标 Z i , j Z_{i,j} Zi,j和 h i j h_{ij} hij有如下关系 Z i , j = − h i j ( 5 ) Z_{i,j}=-h_{ij} \qquad\qquad(5) Zi,j=−hij(5) 因此(4)式可以替换为 e s ⃗ = ( − x i j Z i , j , 0 , − 1 ) ( 6 ) \vec{e_s}=(-\frac{x_{ij}}{Z_{i,j}},0,-1) \qquad\qquad(6) es=(−Zi,jxij,0,−1)(6)
即 p s = − x i j Z i , j , q s = 0 p_s=-\frac{x_{ij}}{Z_{i,j}},q_s=0 ps=−Zi,jxij,qs=0
与此同时,根据有限差分方法, e ⃗ \vec{e} e也有如下表达 e ⃗ = ( Z i , j − Z i − 1 , j , Z i , j − Z i , j − 1 , − 1 ) ( 7 ) \vec{e}=(Z_{i,j}-Z_{i-1,j},Z_{i,j}-Z_{i,j-1},-1)\qquad\qquad(7) e=(Zi,j−Zi−1,j,Zi,j−Zi,j−1,−1)(7)
即 p = ∂ Z ∂ x = Z i , j − Z i − 1 , j , q = ∂ Z ∂ y = Z i , j − Z i , j − 1 p=\frac{\partial{Z}}{\partial{x}}=Z_{i,j}-Z_{i-1,j},q=\frac{\partial{Z}}{\partial{y}}=Z_{i,j}-Z_{i,j-1} p=∂x∂Z=Zi,j−Zi−1,j,q=∂y∂Z=Zi,j−Zi,j−1
需要注意的是,(i,j)是坐标,对于低精度重建,可以取离散量,这样只需要一个初始化量。而对于高精度重建,应当取<1的离散量,需要一组初始化量。对于重建问题,我们可以以一像素(pixel)为一个运算单位,最后把高度Z用像素关系还原为高度值即可。
将(6)、(7)带入到(2)中并对其进行移项,可以得到 E i j − R ( p , q , p s ) = 0 ( 8 ) E_{ij}-R(p,q,p_s)=0\qquad\qquad(8) Eij−R(p,q,ps)=0(8)
E i j − 1 + p p s 1 + p s 2 1 + p 2 + q 2 = 0 ( 9 ) \color{red}E_{ij}-\frac{1+pp_s}{\sqrt{1+p_s^2}\sqrt{1+p^2+q^2}}=0\qquad\qquad(9) Eij−1+ps21+p2+q21+pps=0(9) 令(9)左式为 f ( Z i , j ) f(Z_{i,j}) f(Zi,j)对其在 Z i , j n − 1 Z_{i,j}^{n-1} Zi,jn−1处进行近似泰勒展开,并带入 Z i , j n Z_{i,j}^n Zi,jn,得到 f ( Z i , j n − 1 ) + ( Z i , j n − Z i , j n − 1 ) ⋅ ∂ f ( Z i , j n − 1 ) ∂ Z i , j ≈ 0 ( 10 ) f(Z_{i,j}^{n-1})+(Z_{i,j}^n-Z_{i,j}^{n-1})\cdot\frac{\partial f(Z_{i,j}^{n-1})}{\partial Z_{i,j}}\approx0\qquad\qquad(10) f(Zi,jn−1)+(Zi,jn−Zi,jn−1)⋅∂Zi,j∂f(Zi,jn−1)≈0(10)
移项便可以得到递推公式
Z i , j n = Z i , j n − 1 − f ( Z i , j n − 1 ) ∂ f ( Z i , j n − 1 ) ∂ Z i , j ( 11 ) \color{red}Z_{i,j}^n=Z_{i,j}^{n-1}-\frac{f(Z_{i,j}^{n-1})}{\frac{\partial f(Z_{i,j}^{n-1})}{\partial Z_{i,j}}}\qquad\qquad\qquad(11) Zi,jn=Zi,jn−1−∂Zi,j∂f(Zi,jn−1)f(Zi,jn−1)(11)
其中, ∂ f ( Z i , j n − 1 ) ∂ Z i , j \frac{\partial f(Z_{i,j}^{n-1})}{\partial Z_{i,j}} ∂Zi,j∂f(Zi,jn−1)可由(9)式进行求导得到 ∂ f ( Z i , j n − 1 ) ∂ Z i , j = − ( p s − 1 ) p s 2 + ( Z i , j n − 1 ) 2 1 + p 2 + q 2 − ( p p s − Z i , j n − 1 ) ( Z i , j n − 1 p s 2 + ( Z i , j n − 1 ) 2 ⋅ 1 + p 2 + q 2 + p + q 1 + p 2 + q 2 ⋅ p s 2 + ( Z i , j n − 1 ) 2 ( p s 2 + ( Z i , j n − 1 ) 2 ) ⋅ ( 1 + p 2 + q 2 ) ( 12 ) \color{red}\frac{\partial f(Z_{i,j}^{n-1})}{\partial Z_{i,j}}=-\frac{(p_s-1)\sqrt{p_s^2+(Z_{i,j}^{n-1})^2}\sqrt{1+p^2+q^2}-(pp_s-Z_{i,j}^{n-1})(\frac{Z_{i,j}^{n-1}}{\sqrt{p_s^2+(Z_{i,j}^{n-1})^2}}\cdot\sqrt{1+p^2+q^2}+\frac{p+q}{\sqrt {1+p^2+q^2}}\cdot\sqrt{p_s^2+(Z_{i,j}^{n-1})^2}}{(p_s^2+(Z_{i,j}^{n-1})^2)\cdot(1+p^2+q^2)}\qquad(12) ∂Zi,j∂f(Zi,jn−1)=−(ps2+(Zi,jn−1)2)⋅(1+p2+q2)(ps−1)ps2+(Zi,jn−1)21+p2+q2−(pps−Zi,jn−1)(ps2+(Zi,jn−1)2Zi,jn−1⋅1+p2+q2+1+p2+q2p+q⋅ps2+(Zi,jn−1)2(12)
其中, { p s = x i j (13) p = ∂ Z ∂ x = Z i , j − Z i − 1 , j , q = ∂ Z ∂ y = Z i , j − Z i , j − 1 (14) f ( Z i , j ) (15) \color{red}\begin{cases} p_s=x_{ij}& \text {(13)} \\ p=\frac{\partial{Z}}{\partial{x}}=Z_{i,j}-Z_{i-1,j},q=\frac{\partial{Z}}{\partial{y}}=Z_{i,j}-Z_{i,j-1} & \text{(14)}\\f(Z_{i,j}) &\text{(15)}\end{cases} ⎩⎪⎨⎪⎧ps=xijp=∂x∂Z=Zi,j−Zi−1,j,q=∂y∂Z=Zi,j−Zi,j−1f(Zi,j)(13)(14)(15)
至此,已经完成了Tsai的SFS线性化方法在SSS中的应用转换,主要依托红色公式进行迭代运算,而Tsai在论文中说初始化可以都给0,同时仅需要2轮的迭代就可以完成形状重建,至于其实现思路,我们在下一节进行详细阐述。
4、本算法的程序实现思路
我们简单总结一下以上红色的重要公式,特别是迭代过程,我们分析一下可以发现,(11)式中,像素坐标为(i,j)的点下一次迭代的像素高度 Z i , j n Z_{i,j}^n Zi,jn取决于:的 Z i , j n − 1 Z_{i,j}^{n-1} Zi,jn−1, E i j , x i j , Z i − 1 , j n − 1 , Z i , j − 1 n − 1 E_{ij},x_{ij},Z_{i-1,j}^{n-1},Z_{i,j-1}^{n-1} Eij,xij,Zi−1,jn−1,Zi,j−1n−1
在Tsai的论文中提到,此类方法做一到两次迭代就已经足够,此外迭代完成后对深度图可以加入高斯平滑处理,以优化最终结果。根据Tsai的论文提示,一开始高度图可以用0做初始化,但由于领域的不同,我们是海底领域,我们一开始用侧扫声呐XTF文件中拖鱼距离海底的高度H的相反数进行全局初始化,
从公式中我们可以看出来, Z i , j Z_{i,j} Zi,j的计算需要 Z i − 1 , j , Z i , j − 1 Z_{i-1,j},Z_{i,j-1} Zi−1,j,Zi,j−1,而我们处理图像大小是有限像素的,因此需要对图像进行行与列的扩充,Ady Ecker的多项式SFS论文中也有提到此类扩充。我们这里给出的扩充算法如下:
首先对矩阵Z使用zini的值(即拖鱼距离海底高度H的相反数)来进行初始化,我们不关心那些位于水柱区的内容,在程序处理时应当跳过。我们尽量在裁剪图片时就选择不包含水柱区的内容。
初始化完毕后我们进行二次迭代,只有扩充列不参加迭代,保留初始化的数值,这样是否精确,该如何更好地初始化将会是我们之后研究的一个重点。
最后我们将结果进行高斯滤波,消除毛刺。
第二次迭代与第一次类同。有了高度图以后我们可以根据点云重建注册等方法进行三维可视化,这将是之后的内容。
需要注意的一点是,由于前文提到的有水柱区的缘故,我们重建时不会遇到完全是矩形区域的图像,这将也是之后的内容。本节仅仅实现一定矩形区域里的SFS,但x的定义是到侧扫声呐的平距(像素单位),需要注意。
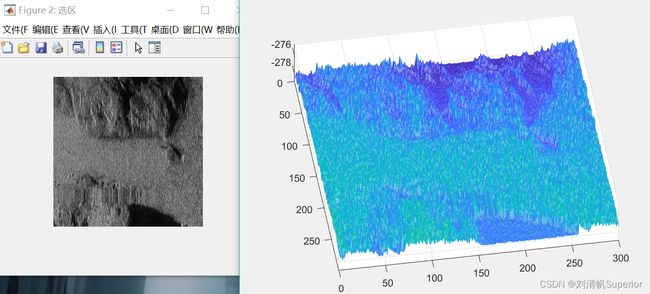
我们在这里展示一下通过 m e s h mesh mesh函数所显示的高度图(未经过滤波和各种点云注册处理)
其实在显示时有个问题困扰了我,后来我发现,matlab mesh坐标矩阵的映射和图像中坐标矩阵的映射不太一样,得到图像坐标矩阵后需要转置一下再mesh才能得到想要的结果。图上一切单位都是归一化的像素,每个像素实际长度等于xm。
在之后的国内赵建虎学者对Tsai方法进行二阶泰勒展开时,我发现赵建虎除了和Tsai一样把 Z i , j Z_{i,j} Zi,j看做变量之外,也将 Z i − 1 , j Z_{i-1,j} Zi−1,j和 Z i , j − 1 Z_{i,j-1} Zi,j−1看做变量,进行多元泰勒公式的展开。这样做虽然增加了运算的复杂度,但是有一个好处就是,对图像每一轮的迭代过程中,一点除了受到上一轮本点值的影响,还受到本轮临近点的影响,增加了反馈因子和反馈速度,可以提高准确度,避免误差在大范围内传播。
参考文献比较多,只罗列主要参考文献
[1]Tsai P S, Shah M. A fast linear shape from shading[C]//Proceedings
1992 IEEE Computer Society Conference on Computer Vision and Pattern
Recognition. IEEE Computer Society, 1992: 734,735,736-734,735,736.
[2]赵建虎,尚晓东,张红梅. 侧扫声呐图像反演海底地形的一种线性算法[J]. 哈尔滨工业大学学报,2017,49(5):80-86. DOI:10.11918/j.issn.0367-6234.201508051.