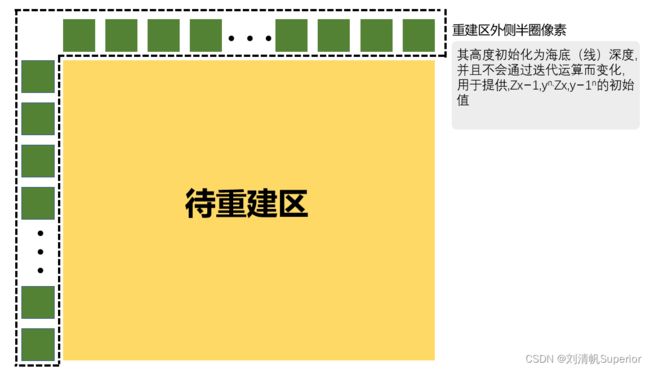
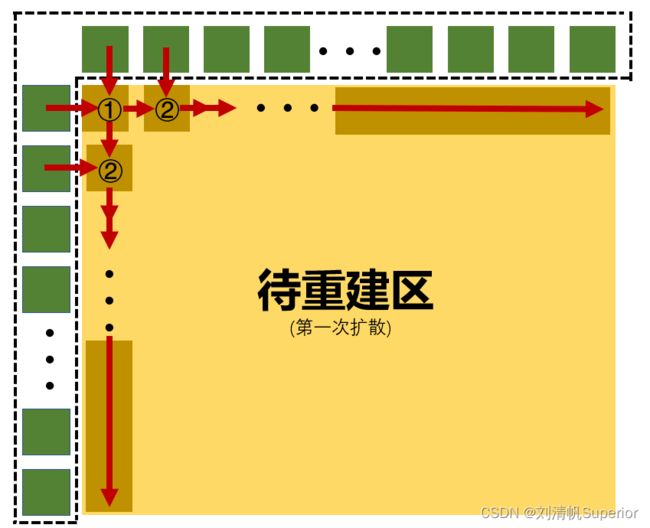
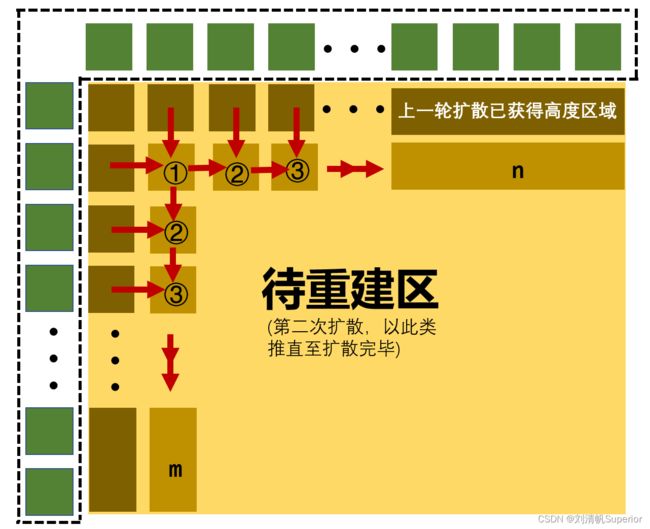
【基于侧扫声呐和SFS方法的地形三维重构】(二)侧扫声呐SFS数学模型建立
本文主要参考文献如下
[1] 赵建虎,尚晓东,张红梅. 侧扫声呐图像反演海底地形的一种线性算法[J]. 哈尔滨工业大学学报,2017,49(5):80-86. DOI:10.11918/j.issn.0367-6234.201508051.
[2] Ruo Zhang, Ping-Sing Tsai, J. E. Cryer and M. Shah, “Shape-from-shading: a survey,” in IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 21, no. 8, pp. 690-706, Aug. 1999, doi: 10.1109/34.784284.
\qquad 这两篇文章前后继承,都是SFS线性化泰勒展开、牛顿迭代的经典算法,只不过Tsai使用了一元泰勒的一阶展开,赵建虎采用了三元泰勒的二阶展开。笔者在阅读以上两者的论文之后比较发现,Tsai的方法虽然表达简洁,但是会造成重建结果不太理想的问题,其明暗图中直接获取的灰度值作为线性主部的主成分过高,使得重建结果好像直接从明暗图中直接按照明暗强度绘制高度一样。而赵建虎学者的方法使用二阶展开,其表达过于繁琐,在使用时(特别还要结合侧扫声呐物理特性),会导致容易出现错误。因此,结合以上两人,笔者想要使用三变量一阶展开的侧扫声呐SFS模型,下面进行具体阐述。
一、公式推导
\qquad 根据朗伯反射原理,我们可以得到后向归一化散射强度E与入射波和反射波夹角余弦成正比,因此我们经过运算可以得到以下公式,具体运算步骤可以参考文献或查看我的文章
https://blog.csdn.net/SuperiorEE/article/details/122909469
0 = f ( x , y ) = E ( x , y ) − 1 + s i n ϕ c o s ϕ ⋅ ( Z x , y − Z x − 1 , y ) ( s i n ϕ c o s ϕ ) 2 + 1 ⋅ ( Z x , y − Z x − 1 , y ) 2 + ( Z x , y − Z x , y − 1 ) 2 + 1 0=f(x,y)=E(x,y)-\frac {1+\frac{sin \phi}{cos \phi}\cdot(Z_{x,y}-Z_{x-1,y})} {\sqrt{(\frac{sin \phi}{cos \phi})^2+1}\cdot\sqrt{(Z_{x,y}-Z_{x-1,y})^2+(Z_{x,y}-Z_{x,y-1})^2+1}} 0=f(x,y)=E(x,y)−(cosϕsinϕ)2+1⋅(Zx,y−Zx−1,y)2+(Zx,y−Zx,y−1)2+11+cosϕsinϕ⋅(Zx,y−Zx−1,y) \qquad 当我们固定(x,y)为某一个特定点时, x , y x,y x,y就成为了常量,我们就可以采用主元法将 f f f重新看为三元函数 f ( Z x , y , Z x − 1 , y , Z x , y − 1 ) f(Z_{x,y},Z_{x-1,y},Z_{x,y-1}) f(Zx,y,Zx−1,y,Zx,y−1),而其他的量如 E ( x , y ) E(x,y) E(x,y)为常量。
\qquad 将上式根据泰勒公式展开得到
0 ≈ F ( 0 ) + F ( 1 ) 0 \approx F(0)+F(1) 0≈F(0)+F(1) \qquad 其中, F ( 0 ) = f ( Z x , y n − 1 , Z x − 1 , y n − 1 , Z x , y − 1 n − 1 ) F(0)=f({Z_{x,y}}^{n-1},{Z_{x-1,y}}^{n-1},{Z_{x,y-1}}^{n-1}) F(0)=f(Zx,yn−1,Zx−1,yn−1,Zx,y−1n−1) F ( 1 ) = ∂ f ∂ Z x , y ∣ Z x , y n − 1 , Z x − 1 , y n − 1 , Z x , y − 1 n − 1 ⋅ ( Z x , y n − Z x , y n − 1 ) + ∂ f ∂ Z x − 1 , y ∣ Z x , y n − 1 , Z x − 1 , y n − 1 , Z x , y − 1 n − 1 ⋅ ( Z x − 1 , y n − Z x − 1 , y n − 1 ) + ∂ f ∂ Z x , y − 1 ∣ Z x , y n − 1 , Z x − 1 , y n − 1 , Z x , y − 1 n − 1 ⋅ ( Z x , y − 1 n − Z x , y − 1 n − 1 ) F(1)={\frac{\partial f}{\partial Z_{x,y}} \bigg |}_{{Z_{x,y}}^{n-1},{Z_{x-1,y}}^{n-1},{Z_{x,y-1}}^{n-1}}\cdot ({Z_{x,y}}^{n}-{Z_{x,y}}^{n-1}) +\\ {\frac{\partial f}{\partial Z_{x-1,y}} \bigg |}_{{Z_{x,y}}^{n-1},{Z_{x-1,y}}^{n-1},{Z_{x,y-1}}^{n-1}}\cdot ({Z_{x-1,y}}^{n}-{Z_{x-1,y}}^{n-1}) +\\ {\frac{\partial f}{\partial Z_{x,y-1}} \bigg |}_{{Z_{x,y}}^{n-1},{Z_{x-1,y}}^{n-1},{Z_{x,y-1}}^{n-1}}\cdot ({Z_{x,y-1}}^{n}-{Z_{x,y-1}}^{n-1}) F(1)=∂Zx,y∂f∣∣∣∣Zx,yn−1,Zx−1,yn−1,Zx,y−1n−1⋅(Zx,yn−Zx,yn−1)+∂Zx−1,y∂f∣∣∣∣Zx,yn−1,Zx−1,yn−1,Zx,y−1n−1⋅(Zx−1,yn−Zx−1,yn−1)+∂Zx,y−1∂f∣∣∣∣Zx,yn−1,Zx−1,yn−1,Zx,y−1n−1⋅(Zx,y−1n−Zx,y−1n−1)
\qquad 附上多元泰勒公式:

\qquad 解释:对 f ( Z x , y , Z x − 1 , y , Z x , y − 1 ) f({Z_{x,y}},{Z_{x-1,y}},{Z_{x,y-1}}) f(Zx,y,Zx−1,y,Zx,y−1)按照三元函数泰勒展开形式在 ( Z x , y n − 1 , Z x − 1 , y n − 1 , Z x , y − 1 n − 1 ) ({Z_{x,y}}^{n-1},{Z_{x-1,y}}^{n-1},{Z_{x,y-1}}^{n-1}) (Zx,yn−1,Zx−1,yn−1,Zx,y−1n−1)的临近进行展开,并带入点 ( Z x , y n , Z x − 1 , y n , Z x , y − 1 n ) ({Z_{x,y}}^{n},{Z_{x-1,y}}^{n},{Z_{x,y-1}}^{n}) (Zx,yn,Zx−1,yn,Zx,y−1n),当 ( Z x , y n , Z x − 1 , y n , Z x , y − 1 n ) ({Z_{x,y}}^{n},{Z_{x-1,y}}^{n},{Z_{x,y-1}}^{n}) (Zx,yn,Zx−1,yn,Zx,y−1n)和 ( Z x , y n − 1 , Z x − 1 , y n − 1 , Z x , y − 1 n − 1 ) ({Z_{x,y}}^{n-1},{Z_{x-1,y}}^{n-1},{Z_{x,y-1}}^{n-1}) (Zx,yn−1,Zx−1,yn−1,Zx,y−1n−1)充分接近时,函数值 f f f会收敛到0.
\qquad 适当移项,即可得到牛顿迭代表达式: Z x , y n = Z x , y n − 1 − F ( 0 ) + ∂ f ∂ Z x − 1 , y ∣ Z x , y n − 1 , Z x − 1 , y n − 1 , Z x , y − 1 n − 1 ⋅ ( Z x − 1 , y n − Z x − 1 , y n − 1 ) + ∂ f ∂ Z x , y − 1 ∣ Z x , y n − 1 , Z x − 1 , y n − 1 , Z x , y − 1 n − 1 ⋅ ( Z x , y − 1 n − Z x , y − 1 n − 1 ) ∂ f ∂ Z x , y ∣ Z x , y n − 1 , Z x − 1 , y n − 1 , Z x , y − 1 n − 1 {Z_{x,y}}^{n} ={Z_{x,y}}^{n-1}-\frac {F(0)+\\ {\frac{\partial f}{\partial Z_{x-1,y}} \bigg |}_{{Z_{x,y}}^{n-1},{Z_{x-1,y}}^{n-1},{Z_{x,y-1}}^{n-1}}\cdot ({Z_{x-1,y}}^{n}-{Z_{x-1,y}}^{n-1}) +\\ {\frac{\partial f}{\partial Z_{x,y-1}} \bigg |}_{{Z_{x,y}}^{n-1},{Z_{x-1,y}}^{n-1},{Z_{x,y-1}}^{n-1}}\cdot ({Z_{x,y-1}}^{n}-{Z_{x,y-1}}^{n-1})}{{\frac{\partial f}{\partial Z_{x,y}} \bigg |}_{{Z_{x,y}}^{n-1},{Z_{x-1,y}}^{n-1},{Z_{x,y-1}}^{n-1}}} Zx,yn=Zx,yn−1−∂Zx,y∂f∣∣∣∣Zx,yn−1,Zx−1,yn−1,Zx,y−1n−1F(0)+∂Zx−1,y∂f∣∣∣∣Zx,yn−1,Zx−1,yn−1,Zx,y−1n−1⋅(Zx−1,yn−Zx−1,yn−1)+∂Zx,y−1∂f∣∣∣∣Zx,yn−1,Zx−1,yn−1,Zx,y−1n−1⋅(Zx,y−1n−Zx,y−1n−1)
\qquad 其中 f f f的表达式为 f ( Z x , y , Z x − 1 , y , Z x , y − 1 ) = E ( x , y ) − 1 + s i n ϕ c o s ϕ ⋅ ( Z x , y − Z x − 1 , y ) ( s i n ϕ c o s ϕ ) 2 + 1 ⋅ ( Z x , y − Z x − 1 , y ) 2 + ( Z x , y − Z x , y − 1 ) 2 + 1 f(Z_{x,y},Z_{x-1,y},Z_{x,y-1})=E(x,y)-\frac {1+\frac{sin \phi}{cos \phi}\cdot(Z_{x,y}-Z_{x-1,y})}{\sqrt{(\frac{sin \phi}{cos \phi})^2+1}\cdot\sqrt{(Z_{x,y}-Z_{x-1,y})^2+(Z_{x,y}-Z_{x,y-1})^2+1}} f(Zx,y,Zx−1,y,Zx,y−1)=E(x,y)−(cosϕsinϕ)2+1⋅(Zx,y−Zx−1,y)2+(Zx,y−Zx,y−1)2+11+cosϕsinϕ⋅(Zx,y−Zx−1,y) \qquad 并且 ϕ = a r c t a n x H − Z x , y \phi=arc tan\frac{x}{H-Z_{x,y}} ϕ=arctanH−Zx,yx由于考虑到嵌套求导过于复杂,它是入射光参数,这里我选择进行近似忽略,从而有 ϕ = a r c t a n x H − Z x , y n − 1 − h 1 \phi=arc tan\frac{x}{H-Z_{x,y}^{n-1}-h_1} ϕ=arctanH−Zx,yn−1−h1x \qquad 特别注意,Z是从H向上偏移的高度,即距离海底的高度,因此初始化为0,实际高度从H开始算起。h1为声呐拖鱼深度,为正值 附图如下。
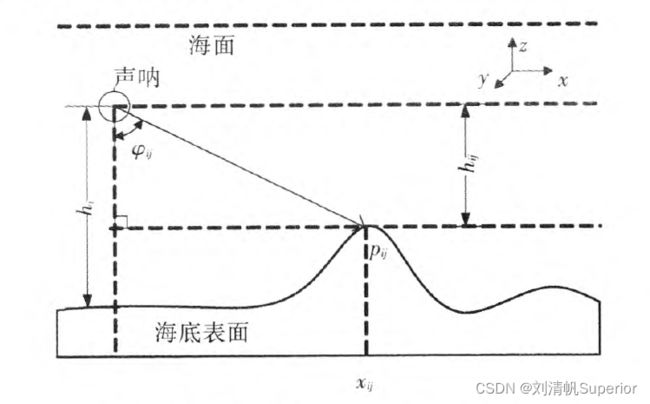
\qquad 如此, ϕ \phi ϕ便可视为与Z无关的常数,来源于之前所存储的数值。这样当我们要计算 ∂ f ∂ Z x , y \frac{\partial f}{\partial Z_{x,y}} ∂Zx,y∂f、 ∂ f ∂ Z x − 1 , y \frac{\partial f}{\partial Z_{x-1,y}} ∂Zx−1,y∂f、 ∂ f ∂ Z x , y − 1 \frac{\partial f}{\partial Z_{x,y-1}} ∂Zx,y−1∂f时求导难度会大大降低。先尝试使用这个简化,如果重建结果理想则完全采纳。
\qquad 计算可得, ∂ f ∂ Z x , y = − s i n ϕ c o s ϕ ⋅ ( Z x , y − 1 2 + Z x , y Z x − 1 , y − Z x , y Z x , y − 1 − Z x − 1 , y Z x , y − 1 + 1 ) − ( 2 Z x , y − Z x − 1 , y − Z x , y − 1 ) ( s i n ϕ c o s ϕ ) 2 + 1 ⋅ [ ( Z x , y − Z x − 1 , y ) 2 + ( Z x , y − Z x , y − 1 ) 2 + 1 ] 3 2 \frac{\partial f}{\partial Z_{x,y}}=-\frac{\frac{sin \phi}{cos \phi}\cdot (Z_{x,y-1}^2+Z_{x,y}Z_{x-1,y}-Z_{x,y}Z_{x,y-1}-Z_{x-1,y}Z_{x,y-1}+1)-(2Z_{x,y}-Z_{x-1,y}-Z_{x,y-1})}{\sqrt{(\frac{sin \phi}{cos \phi})^2+1}\cdot [(Z_{x,y}-Z_{x-1,y})^2+(Z_{x,y}-Z_{x,y-1})^2+1]^{\frac{3}{2}}} ∂Zx,y∂f=−(cosϕsinϕ)2+1⋅[(Zx,y−Zx−1,y)2+(Zx,y−Zx,y−1)2+1]23cosϕsinϕ⋅(Zx,y−12+Zx,yZx−1,y−Zx,yZx,y−1−Zx−1,yZx,y−1+1)−(2Zx,y−Zx−1,y−Zx,y−1) ∂ f ∂ Z x − 1 , y = s i n ϕ c o s ϕ ⋅ ( Z x , y 2 − 2 Z x , y Z x , y − 1 + Z x , y − 1 2 + 1 ) − ( Z x , y − Z x − 1 , y ) ( s i n ϕ c o s ϕ ) 2 + 1 ⋅ [ ( Z x , y − Z x − 1 , y ) 2 + ( Z x , y − Z x , y − 1 ) 2 + 1 ] 3 2 \frac{\partial f}{\partial Z_{x-1,y}}=\frac{\frac{sin \phi}{cos \phi}\cdot (Z_{x,y}^2-2Z_{x,y}Z_{x,y-1}+Z_{x,y-1}^2+1)-(Z_{x,y}-Z_{x-1,y})}{\sqrt{(\frac{sin \phi}{cos \phi})^2+1}\cdot [(Z_{x,y}-Z_{x-1,y})^2+(Z_{x,y}-Z_{x,y-1})^2+1]^{\frac{3}{2}}} ∂Zx−1,y∂f=(cosϕsinϕ)2+1⋅[(Zx,y−Zx−1,y)2+(Zx,y−Zx,y−1)2+1]23cosϕsinϕ⋅(Zx,y2−2Zx,yZx,y−1+Zx,y−12+1)−(Zx,y−Zx−1,y) ∂ f ∂ Z x , y − 1 = − [ 1 + s i n ϕ c o s ϕ ( Z x , y − Z x − 1 , y ) ] ⋅ ( Z x , y − Z x , y − 1 ) ( s i n ϕ c o s ϕ ) 2 + 1 ⋅ [ ( Z x , y − Z x − 1 , y ) 2 + ( Z x , y − Z x , y − 1 ) 2 + 1 ] 3 2 \frac{\partial f}{\partial Z_{x,y-1}}=-\frac{[1+\frac{sin \phi}{cos\phi}(Z_{x,y}-Z_{x-1,y})]\cdot(Z_{x,y}-Z_{x,y-1})}{\sqrt{(\frac{sin \phi}{cos \phi})^2+1}\cdot [(Z_{x,y}-Z_{x-1,y})^2+(Z_{x,y}-Z_{x,y-1})^2+1]^{\frac{3}{2}}} ∂Zx,y−1∂f=−(cosϕsinϕ)2+1⋅[(Zx,y−Zx−1,y)2+(Zx,y−Zx,y−1)2+1]23[1+cosϕsinϕ(Zx,y−Zx−1,y)]⋅(Zx,y−Zx,y−1)
二、计算步骤