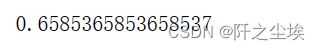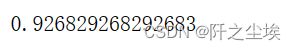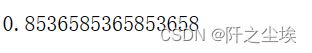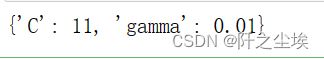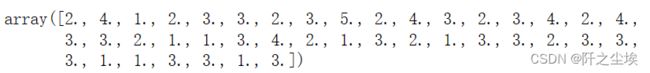Python数据分析案例16——水质检测(支持向量机)

本次带来图片分类的案例，水质检测。

---

数据展示 

五种类别的水质，图片形式储存的：

 前面1是代表水质的类别标签，后面是样本个数。

---

图片特征构建

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import os,re
from PIL import Image
# 图像切割及特征提取
path = '../data/images/'  # 图片所在路径

 # 自定义获取图片名称函数

def getImgNames(path=path):
    '''
    获取指定路径中所有图片的名称
    :param path: 指定的路径
    :return: 名称列表
    '''
    filenames = os.listdir(path)
    imgNames = []
    for i in filenames:
        if re.findall('^\d_\d+\.jpg$', i) != []:
            imgNames.append(i)
    return imgNames

图片数据构建特征：

一般情况下，采集到的水样图像包含盛水容器，且容器的颜色与水体颜色差异较大,同时水体位于图像中央，所以为了提取水色的特征，就需要提取水样图像中央部分具有代表意义的图像，具体实施方式是提取水样图像中央101×101像素的图像。

构建色彩的颜色矩：

三个颜色通道RBG,每个颜色构建三阶特征矩：

 

 

 

 # 批量处理图片数据

imgNames = getImgNames(path=path)  # 获取所有图片名称
n = len(imgNames)        # 图片张数
data = np.zeros([n, 9])  # 用来装样本自变量X,9是9列特征变量
labels = np.zeros([n])   # 用来放样本标签

计算特征，赋值给data：

for i in range(n):
    img = Image.open(path+imgNames[i])  # 读取图片
    M,N = img.size  # 图片像素的尺寸
    img = img.crop((M/2-50,N/2-50,M/2+50,N/2+50))    # 图片切割
    r,g,b = img.split()     # 将图片分割成三通道
    rd = np.asarray(r)/255  # 转化成数组数据
    gd = np.asarray(g)/255
    bd = np.asarray(b)/255

    data[i,0] = rd.mean()  # 一阶颜色矩
    data[i,1] = gd.mean()
    data[i,2] = bd.mean()

    data[i,3] = rd.std()   # 二阶颜色矩
    data[i,4] = gd.std()
    data[i,5] = bd.std()

    data[i,6] = Var(rd)    # 三阶颜色矩
    data[i,7] = Var(gd)
    data[i,8] = Var(bd)

    labels[i] = imgNames[i][0]  # 样本标签

数据准备好了，可以进行机器学习.

---

模型构建

划分训练集测试集

from sklearn.model_selection import train_test_split
# 数据拆分,训练集、测试集
data_tr,data_te,label_tr,label_te = train_test_split(data,labels,test_size=0.2,stratify=labels,random_state=10)
print(data_tr.shape,data_te.shape,label_tr.shape,label_te.shape )

 使用决策树算法试一下分类准确率

from sklearn.tree import DecisionTreeClassifier
model = DecisionTreeClassifier(random_state=5).fit(data_tr, label_tr) 

画混淆矩阵和计算准确率

# 水质评价
from sklearn.metrics import confusion_matrix
pre_te = model.predict(data_te)
# 混淆矩阵
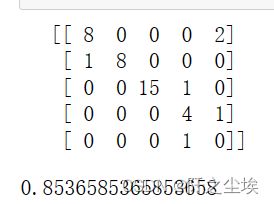
cm_te = confusion_matrix(label_te,pre_te)
print(cm_te)
model.score(data_te,label_te )#准确率

准确率也可以这样计算

from sklearn.metrics import accuracy_score
print(accuracy_score(label_te,pre_te))

 决策树的准确率为85.36%，还行。

---

支持向量机分类

在不使用深度学习算法之前，效果最好的分类算法肯定是支持向量机了，下面使用支持向量机的不同核函数进行分类：

from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import KFold, StratifiedKFold
from sklearn.model_selection import GridSearchCV

from sklearn.svm import SVC

重新划分测试集训练集

X_train, X_test, y_train, y_test = train_test_split(data,labels,stratify=labels,test_size=0.2,random_state=10)
print(X_train.shape, X_test.shape, y_train.shape, y_test.shape )

支持向量机的效果受到数据尺度的影响，要进行数据标准化 

scaler = StandardScaler()
scaler.fit(X_train)
X_train_s = scaler.transform(X_train)
X_test_s = scaler.transform(X_test)

线性核函数

model = SVC(kernel="linear", random_state=123)
model.fit(X_train_s, y_train)
model.score(X_test_s, y_test)

准确率为92.7%

二阶多项式核函数

model = SVC(kernel="poly", degree=2, random_state=123)
model.fit(X_train_s, y_train)
model.score(X_test_s, y_test)

 

 准确率为53.6%，好像不行

三阶多项式核函数

model = SVC(kernel="poly", degree=3, random_state=123)
model.fit(X_train_s, y_train)
model.score(X_test_s, y_test)

 

高斯核函数

model = SVC(kernel="rbf", random_state=123)
model.fit(X_train_s, y_train)
model.score(X_test_s, y_test)

 sigmod核函数

model = SVC(kernel="sigmoid",random_state=123)
model.fit(X_train_s, y_train)
model.score(X_test_s, y_test)

可以看到效果最好的是高斯核函数

下面对高斯核函数进行超参数搜索

param_grid = {'C': [0.001,0.01,0.1, 1,1.5,2,2.5,3,4,5,6,7,8,9,10,11,12,14,16,18,20], 'gamma': [0.001,0.01,0.1, 1,2,3,4,5,6,7,8,9,10]}
kfold = StratifiedKFold(n_splits=5, shuffle=True, random_state=1)
model = GridSearchCV(SVC(kernel="rbf", random_state=123), param_grid, cv=kfold)
model.fit(X_train_s, y_train)

 

最优超参数;

model.best_params_

 

准确率：

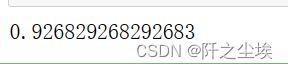
model.score(X_test_s, y_test)

 

准确率好像没怎么变化。支持向量机确实对超参数不是很敏感，调参效果不怎么明显。 

预测：

pred = model.predict(X_test_s)
pred

 

 计算混淆矩阵

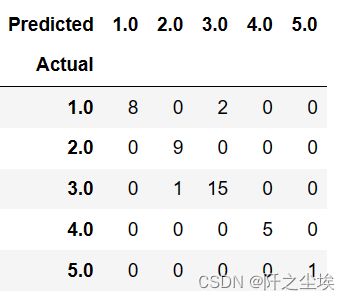
pd.crosstab(y_test, pred, rownames=['Actual'], colnames=['Predicted'])

画混淆矩阵热力图

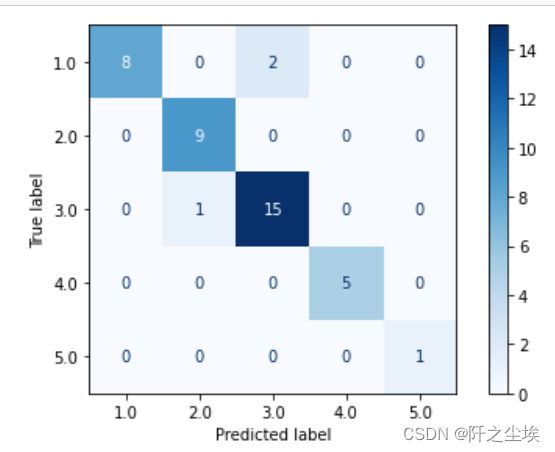
from sklearn.metrics import ConfusionMatrixDisplay
ConfusionMatrixDisplay.from_estimator(model, X_test_s, y_test,cmap='Blues')
plt.tight_layout()