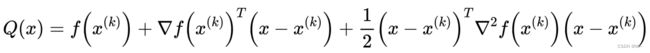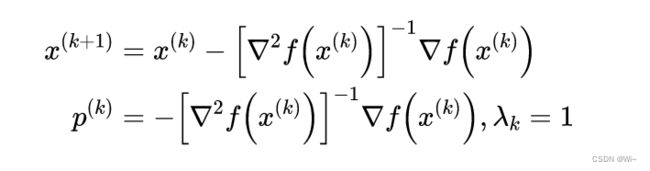牛顿法,高斯牛顿法,列文伯格-马夸尔特(LM)法 (含代码)【最小二乘非线性求解】
文章目录
-
- 一:牛顿法 (Newton's method)
-
- 1:概述
- 2:牛顿方向与牛顿法
- 3:牛顿法的基本步骤
- 4:举例
- 二:高斯牛顿法 (Gauss–Newton algorithm)
-
- 1:概述
- 2:高斯牛顿法推导
- 3:高斯牛顿法算法流程
- 4:高斯牛顿法 C++ 代码
- 三:列文伯格-马夸尔特法(Levenberg-Marquardt algorithm)
-
- 1:概述
- 2:LM算法流程
- 3:列文伯格-马夸尔特法 C++ 代码
- 四:总结
原文链接:http://t.csdn.cn/vZZNF
个人笔记:
牛顿(Newton) 法、高斯牛顿(GaussNewton)法、Levenberg-Marquardt(LM)算法等。结合自己需要实现功能的目的,下面主要给出推导结果、代码实现和实际一些应用。推导过程最后会放一些个人参考的一些文章和资料。
一:牛顿法 (Newton’s method)
1:概述
牛顿法是一种函数逼近法,它的基本思想是:在极小点附近用 x ( k ) x^{(k)} x(k)点的二阶泰勒多项式来近似目标函数 f ( x ) f(x) f(x),并用选代点 x ( k ) x^{(k)} x(k)处指向近似二次函数的极小点方向作为搜索方向 p ( k ) p^{(k)} p(k)。
设规划问题 : m i n f ( x ) , x ∈ R n min f(x),x∈R^n minf(x),x∈Rn
其中 f ( x ) f(x) f(x)在点 x ( k ) x^{(k)} x(k)处具有二阶连续偏导数,黑森矩阵 ▽ 2 f ( x ( k ) ) ▽^2f(x^{(k)}) ▽2f(x(k))正定。
现已有 f ( x ) f(x) f(x)极小点的第 k k k级估计值 x ( k ) x^{(k)} x(k),并将 f ( x ) f(x) f(x)作二阶泰勒展开:
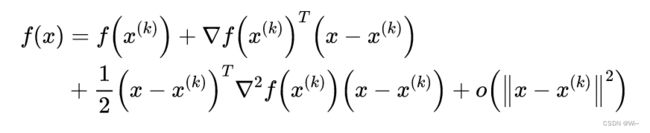 其中主要的是前三项,最后一项为高阶无穷小。
其中主要的是前三项,最后一项为高阶无穷小。
2:牛顿方向与牛顿法
在 x ( k ) x^{(k)} x(k)附近可用 Q ( x ) Q(x) Q(x)来近似 f ( x ) f(x) f(x), Q ( x ) ≈ f ( x ) Q(x) ≈ f(x) Q(x)≈f(x)。
故可以用 Q ( x ) Q(x) Q(x)的极小点来近似 f ( x ) f(x) f(x)的极小点,求 Q ( x ) Q(x) Q(x)的驻点:
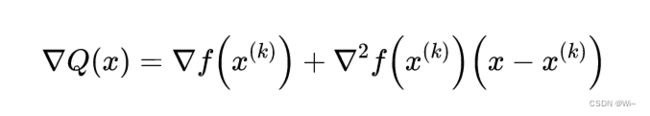
由梯度 ▽ Q ( x ) = 0 ▽Q(x) = 0 ▽Q(x)=0得 Q ( x ) Q(x) Q(x)的平稳点 x ( k + 1 ) x^{(k+1)} x(k+1), p ( k ) p^{(k)} p(k)是牛顿方向,步长 λ k \lambda _k λk为 1 1 1
3:牛顿法的基本步骤
1:选取初始数据:初始点 x ( 0 ) x^{(0)} x(0),终止条件 ε > 0 ε>0 ε>0,令 k : = 0 k:=0 k:=0
2:求梯度向量 ▽ f ( k ) ▽f^{(k)} ▽f(k),并计算 ∣ ∣ ▽ f ( k ) ∣ ∣ ||▽f^{(k)}|| ∣∣▽f(k)∣∣:
若 ∣ ∣ ▽ f ( k ) ∣ ∣ < ε ||▽f^{(k)}||<ε ∣∣▽f(k)∣∣<ε,停止选代,输出 x ( k ) x^{(k)} x(k),否则转下一步。
计算 x ( k + 1 ) = x ( k ) + p ( k ) x^{(k+1)} = x^{(k)} + p^{(k)} x(k+1)=x(k)+p(k),以 x ( k + 1 ) x^{(k+1)} x(k+1)作为下一轮迭代点,令 k : = k + 1 k := k+1 k:=k+1,转第2步。
4:举例
试用牛顿法求函数 f ( x ) = x 1 2 + 25 x 2 2 f(x) = x_1^2 + 25x_2^2 f(x)=x12+25x22 的极小点,其中初始点为 x ( 0 ) = ( 2 , 2 ) T x^{(0)} = (2, 2)^T x(0)=(2,2)T, ε = 1 0 − 6 ε = 10^{-6} ε=10−6.
解(1)求梯度和黑塞矩阵:

(2)确定牛顿方向:
 即: x 1 = 0 , x 2 = 0 x_1 = 0,x_2=0 x1=0,x2=0
即: x 1 = 0 , x 2 = 0 x_1 = 0,x_2=0 x1=0,x2=0
这里使用三维坐标系来查看 x 1 = 0 , x 2 = 0 x_1 = 0,x_2=0 x1=0,x2=0存在极值

这里说一下,牛顿法使用黑塞矩阵有个缺点:计算量特别大。下面引出高斯牛顿法是在牛顿法的基础上用雅可比矩阵代替了黑森矩阵。
二:高斯牛顿法 (Gauss–Newton algorithm)
1:概述
高斯-牛顿算法用于求解非线性最小二乘问题,相当于最小化函数值的平方和。它是牛顿求非线性函数最小值方法的扩展。由于平方和必须是非负的,因此该算法可以看作是使用牛顿法迭代地逼近和的零点,从而使和最小化。它的优点是不需要计算可能具有挑战性的二阶导数(也就是黑塞矩阵)。
注意:高斯牛顿法针对非线性最小二乘问题。最小二乘详解
2:高斯牛顿法推导
①:目标函数问题:自变量 x x x 经过模型函数得出因变量 y y y, m m m个观测点:
X = [ x 1 , x 2 , . . . x m ] T X=[x_1,x_2,...x_m]^T X=[x1,x2,...xm]T, Y = [ y 1 , y 2 , . . . y m ] T Y=[y_1,y_2,...y_m]^T Y=[y1,y2,...ym]T
②:模型函数: Y = f ( X ; β 1 , β 2 , . . . , β n ) Y = f(X;β_1,β_2,...,β_n) Y=f(X;β1,β2,...,βn) => f ( x ; β ) f(x;β) f(x;β)
其中 x x x 是自变量 , y y y 是因变量, β β β 是目标参数。 x 和 y x和y x和y是已知的,优化 β β β 目标参数。
③:优化目标函数: m i n S = ∑ i = 1 n ( f ( x i ; β ) − y i ) 2 min S = \displaystyle\sum_{i=1}^{n}(f(x_i;β)-y_i)^2 minS=i=1∑n(f(xi;β)−yi)2
④:第 i i i 次观测点的预测偏差: r i = f ( x i ; β ) − y i ) 2 r_i = f(x_i;β)-y_i)^2 ri=f(xi;β)−yi)2,那么每次的偏差组成一个向量形式: R = [ r 1 , r 2 , . . . r m ] T R = [r_1,r_2,...r_m]^T R=[r1,r2,...rm]T
⑤:对于③目标函数 可以写成: m i n S = ∑ i = 1 n r i 2 = R T R min S = \displaystyle\sum_{i=1}^{n}r_i^2 = R^TR minS=i=1∑nri2=RTR
⑥:那么目标函数梯度: ▽ S ( β ) = [ ∂ S ∂ β 1 , ∂ S ∂ β 2 , . . . , ∂ S ∂ β n ] T ▽S(β) = [\frac{\partial S}{\partial β_1},\frac{\partial S}{\partial β_2},...,\frac{\partial S}{\partial β_n}]^T ▽S(β)=[∂β1∂S,∂β2∂S,...,∂βn∂S]T,其中对每个参数 β j β_j βj 求偏导 ∂ S ∂ β j = 2 ∑ i = 1 m r i ∂ r i ∂ β j \frac{\partial S}{\partial β_j} = 2 \displaystyle\sum_{i=1}^{m}r_i\frac{\partial r_i}{\partial β_j} ∂βj∂S=2i=1∑mri∂βj∂ri
⑦:对于 R = [ r 1 , r 2 , . . . r m ] T 和 β R = [r_1,r_2,...r_m]^T和β R=[r1,r2,...rm]T和β的偏导形式就可以写成 雅可比矩阵
J ( R ( β ) ) = [ ∂ r 1 ∂ β 1 . . . ∂ r 1 ∂ β n ⋮ ⋱ ⋮ ∂ r m ∂ β 1 . . . ∂ r m ∂ β n ] J(R(β)) = \begin{bmatrix} \frac{\partial r_1}{\partial β_1}&...&\frac{\partial r_1}{\partial β_n}\\ \vdots & \ddots & \vdots \\ \frac{\partial r_m}{\partial β_1}&...&\frac{\partial r_m}{\partial β_n}\end{bmatrix} J(R(β))= ∂β1∂r1⋮∂β1∂rm...⋱...∂βn∂r1⋮∂βn∂rm
⑧:目标函数梯度(一阶偏导): ▽ S ( β ) = [ ∂ S ∂ β 1 , ∂ S ∂ β 2 , . . . , ∂ S ∂ β n ] T = > ∂ S ∂ β j = 2 ∑ i = 1 m r i ∂ r i ∂ β j = > ▽ S = 2 J T R ▽S(β) = [\frac{\partial S}{\partial β_1},\frac{\partial S}{\partial β_2},...,\frac{\partial S}{\partial β_n}]^T => \frac{\partial S}{\partial β_j} = 2 \displaystyle\sum_{i=1}^{m}r_i\frac{\partial r_i}{\partial β_j} => ▽S = 2J^TR ▽S(β)=[∂β1∂S,∂β2∂S,...,∂βn∂S]T=>∂βj∂S=2i=1∑mri∂βj∂ri=>▽S=2JTR
⑨:求目标函数黑塞矩阵(二阶偏导):
由梯度向量元素 ∂ S ∂ β j = 2 ∑ i = 1 m r i ∂ r i ∂ β j \frac{\partial S}{\partial β_j} = 2 \displaystyle\sum_{i=1}^{m}r_i\frac{\partial r_i}{\partial β_j} ∂βj∂S=2i=1∑mri∂βj∂ri 到黑塞矩阵元素 ∂ 2 S ∂ β k ∂ β j = 2 ∂ ∂ β k ( ∑ i = 1 m r i ∂ r i ∂ β j ) \frac{\partial ^2S}{\partial β_k\partial β_j} = 2\frac{\partial }{\partial β_k} (\displaystyle\sum_{i=1}^{m}r_i\frac{\partial r_i}{\partial β_j}) ∂βk∂βj∂2S=2∂βk∂(i=1∑mri∂βj∂ri),
应用链式法则得: ∂ 2 S ∂ β k ∂ β j = 2 ∑ i = 1 m ( ∂ r i ∂ β k ∂ r i ∂ β j + r i ∂ 2 r i ∂ β k ∂ β j ) \frac{\partial ^2S}{\partial β_k\partial β_j} = 2 \displaystyle\sum_{i=1}^{m}(\frac{\partial r_i}{\partial β_k}\frac{\partial r_i}{\partial β_j} + r_i\frac{\partial^2 r_i}{\partial β_k\partial β_j}) ∂βk∂βj∂2S=2i=1∑m(∂βk∂ri∂βj∂ri+ri∂βk∂βj∂2ri),
其中 O O O矩阵元素 : O k j = ∑ i = 1 m r i ∂ 2 r i ∂ β k ∂ β j O_{kj} = \displaystyle\sum_{i=1}^{m}r_i\frac{\partial^2 r_i}{\partial β_k\partial β_j} Okj=i=1∑mri∂βk∂βj∂2ri
黑塞矩阵: H = 2 ( J T J + O ) H = 2(J^TJ + O) H=2(JTJ+O)
⑩:写成牛顿法形式:如果模型比较好,其中 O O O矩阵 r i r_i ri是趋近于0的。这里就把 O O O矩阵忽略掉,方便计算。

3:高斯牛顿法算法流程
1:给定初始参数值 β 0 β_0 β0 (默认是为 1 1 1 的向量)。设 ε = 1 − 10 ε = 1^{-10} ε=1−10
2:对于第 k k k 次选代,求出当前的雅可比矩阵 J ( β k ) J(β_k) J(βk) 和残差值 f ( β k ) f(β_k) f(βk)也就是 R R R。
3:求解增量方程: H Δ β k = − g H\Delta β_k = -g HΔβk=−g
=> Δ β k = − H − 1 g \Delta β_k= -H^{-1}g Δβk=−H−1g
=> Δ β k ≈ − ( J T J ) − 1 J T R \Delta β_k≈ -(J^TJ)^{-1}J^TR Δβk≈−(JTJ)−1JTR 。这里用雅可比矩阵 J T J J^TJ JTJ 近似黑塞矩阵 H H H。
4:若 Δ β k < ε \Delta β_k<ε Δβk<ε ,则停止。否则,令 β k + 1 = β k + Δ β k β_{k+1} = β_k +\Delta β_k βk+1=βk+Δβk,返回第2步。
4:高斯牛顿法 C++ 代码
/* 高斯牛顿法(GNA) 解决非线性最小二乘问题 确定目标函数和约束来对现有的参数优化
*/
template <class _T,class _ResidualsVector,class _JacobiMat>
Eigen::VectorXd GaussNewtonAlgorithm(Eigen::VectorXd params,_T otherArgs, _ResidualsVector ResidualsVector,_JacobiMat JacobiMat,double _epsilon = 1e-10,int _maxIteCount = 999)
{
int k=0;
// ε 终止条件
double epsilon = _epsilon;
//迭代次数
int maxIteCount = _maxIteCount;
//found 为true 结束循环
bool found = false;
while(!found && k<maxIteCount)
{
//迭代增加
k++;
//获取预测偏差值 r= ^y(预测值) - y(实际值)
//保存残差值
Eigen::VectorXd residual = ResidualsVector(params,otherArgs);
//求雅可比矩阵
Eigen::MatrixXd Jac = JacobiMat(params,otherArgs);
// Δx = - (Jac^T * Jac)^-1 * Jac^T * r
Eigen::VectorXd delta_x = - (((Jac .transpose() * Jac ).inverse()) * Jac.transpose() * residual).array();
qDebug()<<QString("高斯牛顿法:第 %1 次迭代 --- 精度:%2 ").arg(k).arg(delta_x.array().abs().sum());
//达到精度,结束
if(delta_x.array().abs().sum() < epsilon)
{
found = true;
}
//x(k+1) = x(k) + Δx
params = params + delta_x;
}
return params;
}
Matrix是Eigen库中的一个矩阵类,这里引入Eigen库方便代数运算。
近似黑塞矩阵 J ( x ) T J ( x ) J(x)^TJ(x) J(x)TJ(x)的可能是奇异矩阵或者病态的,下面引出 L M LM LM算法。
三:列文伯格-马夸尔特法(Levenberg-Marquardt algorithm)
1:概述
在数学和计算中,Levenberg–Marquardt 算法(LMA或简称LM),也称为 阻尼最小二乘法( DLS ),用于解决非线性最小二乘法问题。这些最小化问题尤其出现在最小二乘 曲线拟合中。LMA 在高斯-牛顿算法(GNA) 和梯度下降法之间进行插值。LMA 比 GNA更鲁棒,这意味着在许多情况下,即使它开始时离最终最小值很远,它也能找到解决方案。对于性能良好的函数和合理的启动参数,LMA 往往比 GNA 慢。LMA 也可以被视为使用信赖域方法的高斯-牛顿。
LMA 在许多软件应用程序中用于解决一般曲线拟合问题。通过使用高斯-牛顿算法,它通常比一阶方法收敛得更快。然而,与其他迭代优化算法一样,LMA 只能找到局部最小值,不一定是全局最小值。与其他数值最小化算法一样,Levenberg–Marquardt 算法是一个迭代过程。要开始最小化,用户必须提供参数向量的初始猜测 β β β, 在只有一个最小值的情况下,一个不知情的标准猜测就像 β = [ 1 , 1 , . . . , 1 ] T β = [1,1,...,1]^T β=[1,1,...,1]T会工作得很好;在有多个最小值的情况下,只有当初始猜测已经有点接近最终解决方案时,算法才会收敛到全局最小值。
2:LM算法流程
1:给定初始参数值 β 0 β_0 β0 (默认是为 1 1 1 的向量)。初始 μ 0 μ_0 μ0的选择可以依赖于 H 0 = J ( β 0 ) T J ( β 0 ) H_0=J(β_0)^TJ(β_0) H0=J(β0)TJ(β0) 中的元素,一般我们选择 μ 0 = τ ∗ m a x i { H i i ( 0 ) } μ_0 =τ*max_i\{H_{ii}^{(0)}\} μ0=τ∗maxi{Hii(0)},一般 τ = 1 0 − 6 τ=10^{−6} τ=10−6,这里设置 ε 1 = 1 − 10 ε_1 = 1^{-10} ε1=1−10和 ε 2 = 1 − 10 ε_2 = 1^{-10} ε2=1−10。
2:若 ∣ ∣ g ∣ ∣ ∞ ≤ ε 1 ||g||_\infty≤ε_1 ∣∣g∣∣∞≤ε1 成立,则停止。
3:对于第 k k k 次选代,求出当前的雅可比矩阵 J ( β k ) J(β_k) J(βk) 和残差值 f ( β k ) f(β_k) f(βk)也就是 R R R。
4:求解增量方程: ( H + μ k I ) Δ β k = − g (H+μ_kI)\Delta β_k = -g (H+μkI)Δβk=−g
=> Δ β k = − ( H + μ k I ) − 1 g \Delta β_k= -(H+μ_kI)^{-1}g Δβk=−(H+μkI)−1g
=> Δ β k ≈ − ( J T J + μ k I ) − 1 J T R \Delta β_k≈ -(J^TJ+μ_kI)^{-1}J^TR Δβk≈−(JTJ+μkI)−1JTR 。这里用雅可比矩阵 J T J J^TJ JTJ 近似黑塞矩阵 H H H。
5:若 ∣ ∣ Δ β k ∣ ∣ ≤ ε 2 ( ∣ ∣ β k ∣ ∣ + ε 2 ) ||\Delta β_k||≤ε_2(||β_k|| + ε_2) ∣∣Δβk∣∣≤ε2(∣∣βk∣∣+ε2) 成立,则停止。否则,令 β k + 1 = β k + Δ β k β_{k+1} = β_k +\Delta β_k βk+1=βk+Δβk。
6: ρ = ∣ ∣ F ( β k ) ∣ ∣ 2 2 − ∣ ∣ F ( β k + Δ β k ) ∣ ∣ 2 2 L ( 0 ) − L ( Δ β k ) \rho = \frac{||F(β_k)||_2^2-||F(β_k+\Delta β_k)||_2^2}{L(0) - L(\Delta β_k)} ρ=L(0)−L(Δβk)∣∣F(βk)∣∣22−∣∣F(βk+Δβk)∣∣22,如果 ρ > 0 \rho >0 ρ>0,求出当前的黑塞矩阵 H ≈ J ( β k ) T J ( β k ) H ≈ J(β_k)^TJ(β_k) H≈J(βk)TJ(βk) 和梯度 g = J ( β k ) T f ( β k ) g = J(β_k)^Tf(β_k) g=J(βk)Tf(βk)。若 ∣ ∣ g ∣ ∣ ∞ ≤ ε 1 ||g||_\infty≤ε_1 ∣∣g∣∣∞≤ε1 成立,则停止。更新 μ k μ_k μk, μ k = μ k ∗ m a x { 1 3 , 1 − ( 2 ρ − 1 ) 3 } ; v = 2 μ_k =μ_k*max\{\frac{1}{3},1-(2\rho-1)^3\};v=2 μk=μk∗max{31,1−(2ρ−1)3};v=2。如果 ρ ≤ 0 \rho ≤0 ρ≤0, μ k = μ k ∗ v ; v = 2 ∗ v μ_k =μ_k*v; v=2*v μk=μk∗v;v=2∗v。
最终伪代码如下:
3:列文伯格-马夸尔特法 C++ 代码
/* 列文伯格马夸尔特法(LMA) == 使用信赖域的高斯牛顿法,鲁棒性更好, 确定目标函数和约束来对现有的参数优化
* params 初始参数,待优化
* otherArgs 其他参数
* _ResidualsVector 自定义函数:获取预测值和实际值的差值
* _JacobiMat 自定义函数:获取当前的雅可比矩阵
* _epsilon 收敛精度
* _maxIteCount 最大迭代次数
* _epsilon 和 _maxIteCount 达到任意一个条件就停止返回
*/
template <class _T,class _ResidualsVector,class _JacobiMat>
Eigen::VectorXd LevenbergMarquardtAlgorithm(Eigen::VectorXd params,_T otherArgs, _ResidualsVector ResidualsVector,_JacobiMat JacobiMat,double _epsilon = 1e-12,int _maxIteCount = 99)
{
// ε 终止条件
double epsilon = _epsilon;
double currentEpsilon=0.0;
// τ
double tau = 1e-6;
//迭代次数
int maxIteCount = _maxIteCount;
int k=0;
int v=2;
//求雅可比矩阵
Eigen::MatrixXd Jac = JacobiMat(params,otherArgs);
//用雅可比矩阵近似黑森矩阵
Eigen::MatrixXd Hessen = Jac .transpose() * Jac ;
//获取预测偏差值 r= ^y(预测值) - y(实际值)
//保存残差值
Eigen::VectorXd residual = ResidualsVector(params,otherArgs);
//梯度
Eigen::MatrixXd g = Jac.transpose() * residual;
//found 为true 结束循环
bool found = ( g.lpNorm<Eigen::Infinity>() <= epsilon );
//阻尼参数μ
double mu = tau * Hessen.diagonal().maxCoeff();
while(!found && k<maxIteCount)
{
k++;
qDebug()<<QString("LMA:第 %1 次迭代 --- 精度:%2 ").arg(k).arg(currentEpsilon);
//LM方向 uI => I 用黑森矩阵对角线代替
//Eigen::MatrixXd delta_x = - (Hessen + mu*Hessen.asDiagonal().diagonal()).inverse() * g;
Eigen::VectorXd delta_x = - (Hessen + mu*Eigen::MatrixXd::Identity(Hessen.cols(), Hessen.cols())).inverse() * g;
if( delta_x.lpNorm<2>() <= epsilon * (params.lpNorm<2>() + epsilon ))
{
qDebug()<<QString("LMA:第 %1 次迭代 --- 精度:%2 ").arg(k).arg(delta_x.lpNorm<2>());
found = true;
}
else
{
Eigen::VectorXd newParams = params + delta_x;
//L(0) - L(delta) = 0.5*(delta^-1)*(μ*delta - g)
//ρ = (F(x) - F(x_new)) / (L(0) - L(delta));
double rho = (ResidualsVector(params,otherArgs).array().pow(2).sum() - ResidualsVector(newParams,otherArgs).array().pow(2).sum())
/ (0.5*delta_x.transpose()*(mu * delta_x - g)).sum();
if(rho>0)
{
params = newParams;
Jac = JacobiMat(params,otherArgs);
Hessen = Jac.transpose() * Jac ;
residual = ResidualsVector(params,otherArgs);
g = Jac.transpose() * residual;
currentEpsilon = g.lpNorm<Eigen::Infinity>();
found = (currentEpsilon <= epsilon );
mu = mu* qMax(1/3.0 , 1-qPow(2*rho -1,3));
v=2;
}
else
{
mu = mu*v;
v = 2*v;
}
}
}
return params;
}
//====================================================================
//====================================================================
// 例子:下面是曲线拟合使用lm算法来优化,残差值向量和雅可比矩阵需要自己编写
#define DERIV_STEP 1e-5
//线拟合残差值向量
class LineFitResidualsVector
{
public:
Eigen::VectorXd operator()(const Eigen::VectorXd& parameter,const QList<Eigen::MatrixXd> &otherArgs)
{
Eigen::MatrixXd inValue = otherArgs.at(0);
Eigen::VectorXd outValue = otherArgs.at(1);
int dataCount = inValue.rows();
int paramsCount = parameter.rows();
//保存残差值
Eigen::VectorXd residual = Eigen::VectorXd::Zero(dataCount);
//获取预测偏差值 r= ^y(预测值) - y(实际值)
for(int i=0;i<dataCount;++i)
{
for(int j=0;j<paramsCount;++j)
{
//这里使用曲线方程 y = a1*x^0 + a2*x^1 + a3*x^2 + ... 根据参数(a1,a2,a3,...)个数来设置
residual(i) += parameter(j) * inValue(i,j);
}
}
return residual - outValue;
}
};
//求线拟合雅克比矩阵 -- 通过计算求偏导
class LineFitJacobi
{
//求偏导
double PartialDeriv(const Eigen::VectorXd& parameter,int paraIndex,const Eigen::MatrixXd &inValue,int objIndex)
{
Eigen::VectorXd para1 = parameter;
Eigen::VectorXd para2 = parameter;
para1(paraIndex) -= DERIV_STEP;
para2(paraIndex) += DERIV_STEP;
//逻辑
double obj1 = 0;
double obj2 = 0;
for(int i=0;i<parameter.rows();++i)
{
//这里使用曲线方程 y = a1*x^0 + a2*x^1 + a3*x^2 + ... 根据参数(a1,a2,a3,...)个数来设置
obj1 += para1(i) * inValue(objIndex,i);
}
for(int i=0;i<parameter.rows();++i)
{
//这里使用曲线方程 y = a1*x^0 + a2*x^1 + a3*x^2 + ... 根据参数(a1,a2,a3,...)个数来设置
obj2 += para2(i) * inValue(objIndex,i);
}
return (obj2 - obj1) / (2 * DERIV_STEP);
}
public:
Eigen::MatrixXd operator()(const Eigen::VectorXd& parameter,const QList<Eigen::MatrixXd> &otherArgs)
{
Eigen::MatrixXd inValue = otherArgs.at(0);
int rowNum = inValue.rows();
int paramsCount = parameter.rows();
Eigen::MatrixXd Jac(rowNum, paramsCount);
for (int i = 0; i < rowNum; i++)
{
for (int j = 0; j < paramsCount; j++)
{
Jac(i,j) = PartialDeriv(parameter,j,inValue,i);
}
}
return Jac;
}
};
/* y = a0 * x^0 + a1 * x^1 求未知系数a0和a1\n"
* y = a0 * x^0 + a1 * x^1 + a2 * x^2 求未知系数a0和a1和a2\n"
* y = a0 * x^0 + a1 * x^1 + a2 * x^2 + a3 * x^3 求未知系数a0和a1和a2和a3\n"
*
* 矩阵描述
* _ _ _ _ _ _
* |1 x1 x1^2 ...| | a0 | |y1 |
* |1 x2 x2^2 ...| | a1 | =|y2 |
* |1 x3 x3^2 ...| | a2 | |y3 |
* |1 x4 x4^2 ...| | .. | |y4 |
* |.... ...| - - |...|
* - - - -
* Ax = B
*/
QList<double> coeffL;
//数据个数
int rows = listP.count();
int col = m_maxPower + 1;
//m_maxPower
VectorXd vector_x;
//创建动态n行,3列矩阵
MatrixXd matA;
matA.resize(rows,col);
VectorXd matB;
matB.resize(rows,1);
//构建矩阵
for(int i=0;i<rows;++i)
{
//A
for(int j=0;j<col;++j)
{
matA(i,j) = std::pow(listP.at(i).x(),j);
}
//B
matB(i,0) = listP.at(i).y();
}
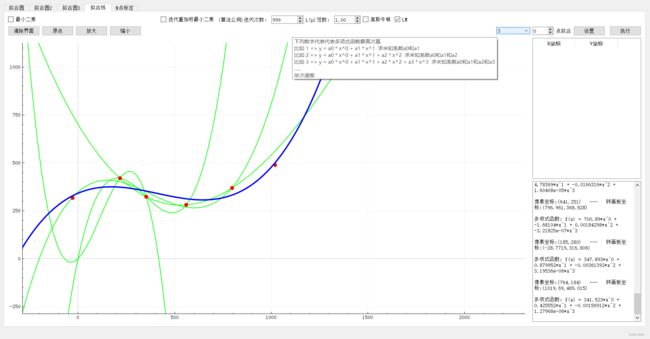
//勾选高斯牛顿法
if(m_GN->isChecked())
{
int iteCount= m_iterationCount->value();
//初始参数为1
VectorXd args = VectorXd::Ones(m_maxPower+1);
QList<MatrixXd> otherArgs;
otherArgs.append(matA);
otherArgs.append(matB);
vector_x =GlobleAlgorithm::getInstance()->GaussNewtonAlgorithm(args,otherArgs,LineFitResidualsVector(),LineFitJacobi(),1e-10,iteCount);
}
//勾选LM
else if(m_LM->isChecked())
{
int iteCount= m_iterationCount->value();
//初始参数为1
VectorXd args = VectorXd::Ones(m_maxPower+1);
QList<MatrixXd> otherArgs;
otherArgs.append(matA);
otherArgs.append(matB);
vector_x =GlobleAlgorithm::getInstance()->LevenbergMarquardtAlgorithm(args,otherArgs,LineFitResidualsVector(),LineFitJacobi(),1e-15,iteCount);
}
四:总结
1:高斯牛顿法和 L M LM LM算法属于优化最小二乘算法,在给定初始参数的情况下,对参数进一步优化,而 L M LM LM算法具有更好的鲁棒性,不过牺牲一定收敛速度为代价的。(优化理解:在数学中,狭义的优化特指一类问题,它有三个要素:优化变量、目标函数、约束。在满足约束的情况下,调整优化变量,使得目标函数的值最小,这就是优化问题最简单的解释)。而牛顿法适用于求极值。
2:工具:主要Qt + Eigen库
Eigen库是一个用于矩阵计算,代数计算库
3:参考文献
黑塞矩阵和雅可比矩阵理解
高斯牛顿法详解
LM算法详解
LM论文