边境的悍匪—机器学习实战:第三章 分类
第三章 分类
文章目录
- 第三章 分类
- 前言
- 一、思维导图
- 二、主要内容
-
- 1、MNIST
- 2、训练二元分类器
- 3、性能测量
- 4、多类分类器
- 5、误差分析
- 6、多标签分类
- 7、多输出分类
- 三、课后练习
- 四、总结
前言
上一章我们了解了如何去完整的完成一个机器学习任务,其中用到了很多的模型。这一章我们将更加深入的了解分类模型,二元分类、多类分类、多标签分类、多输出分类,以及分类模型的性能测量精度/召回率和ROC,最后再对模型使用混淆矩阵进行误差分析。
我们开始吧!
一、思维导图
二、主要内容
1、MNIST
简单的介绍了一下MNIST,他是由人工手写7000张数字的图片,每张图片的有28*28(784)个特征,我们这一章要完成的工作就是训练一个模型能够识别出0-9的数字。
2、训练二元分类器
我们先从简单的二分类问题来入手,判断得到的图片是5还是不是5。第一步和第二章提到的一样的步骤,加载和初步分析数据。
获取与加载数据
用于每次都需要从互联网上获取数据的话非常耗时间且没有网的之后无法运行,我就把数据下载到了本地直接加载。
mnist = loadmat("./data/mnist-original.mat")
X, y = mnist["data"], mnist["label"]
# 对数据进行转换,打乱顺序
all_data = np.vstack((X, y))
all_data = all_data.T
np.random.shuffle(all_data)
X = all_data[:, range(784)]
y = all_data[:, 784]
y = y.astype(np.uint8)
观察和分析数据
之前我们就提到了,这是一张28*28图片,那我们就大概看一下是一张什么的数字图片。
# 显示一张图片
def show_img(data):
"""
显示一张图片
:param data:
:return:
"""
data = data.reshape(28, 28)
plt.imshow(data, cmap=mpl.cm.binary, interpolation="nearest")
plt.axis("off")
one_digit = X[0]
plt.show()
文中还提到了显示多张图片,具体的代码部分我们在git中体现这里只讲过程。
分离训练集和测试集
# 生成测试集和训练集
X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]
# 训练一个二元分类器区分是5和不是5
y_train_5 = (y_train == 5)
y_test_5 = (y_test == 5)
训练一个随机梯度下降二分类器
sgd_clf = SGDClassifier(random_state=42)
sgd_clf.fit(X_train, y_train_5)
print(sgd_clf.predict([one_digit]))
3、性能测量
交叉验证
有了第一个模型之后,我们就需要对和这个模型的性能进行验证,首选我们选用的是上一章提到的交叉验证。并为了得到更高的自由度使用StratifiedKFold来实现自定义的交叉验证。
# 交叉验证
cvs = cross_val_score(sgd_clf, X_train, y_train_5, cv=3, scoring="accuracy")
print(cvs)
# 使用StratifiedKFold自定义交叉验证
sk_fold = StratifiedKFold(n_splits=3, shuffle=True, random_state=42)
for train_index, test_index in sk_fold.split(X_train, y_train_5):
clone_sgd = clone(sgd_clf)
fold_X_train = X_train[train_index]
fold_y_train = y_train_5[train_index]
fold_X_test = X_train[test_index]
fold_y_test = y_train_5[test_index]
clone_sgd.fit(fold_X_train, fold_y_train)
pre_y = clone_sgd.predict(fold_X_test)
num_true = sum(np.array(fold_y_test) == np.array(pre_y))
print(num_true / len(pre_y))
我们可以看到获得了一个很高的准确度,那这个准确度就一定真的准确吗?为了验证这个观点,我们需要自定义个分类器,把所有的数据都分类为不是5然后再来看一下他的准确度。
# 自定义一个分类器分类器的目的是把所有数据都分类为不是5
class Never5Classifier(BaseEstimator):
def fit(self, X, y=None):
pass
def predict(self, X):
return np.zeros((len(X), 1), dtype=bool)
print(sum(y_train_5) / len(y_train_5))
print(len(X_train))
# 交叉验证这个全部为非5的分类器的性能
never_5 = Never5Classifier()
cvs = cross_val_score(never_5, X_train, y_train_5, cv=3, scoring="accuracy")
print(cvs)
我们会发现,我们同样获得了一个高达90%的准确度,是因为5这个数字的数量是占了总数量的10%左右,所以才会出现这个高的准确度,为了能够准确的评估一个分类模型的准确度,我们提出了一个很好的方法 混淆矩阵。
混淆矩阵
我们先来看一下随机梯度下降分类器的混淆矩阵
y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3)
cm = confusion_matrix(y_train_5, y_train_pred)
print(cm)
再看一下一个完美的分类模型的混淆矩阵
# 完美的混淆矩阵
perfect_predictions = y_train_5
cm = confusion_matrix(y_train_5, perfect_predictions)
print(cm)
什么是混淆矩阵?

如图所示,这就是混淆矩阵,左上方为不是5被正确分类的称为真负,左下方为是5但是被错误分类的称为假负,右上方为不是5但是被错误分类的称为假正,右下方为正确分类为5的称为真正。
精度和召回率
精度:所有被分类为正类的实例中,确实为正类的数量占比。
召回率:所有的正例中,被正确分类的数量占比。
sklearn中提供了两个方法来计算这两个值precision_score,recall_score
# 精度与召回率
precision = precision_score(y_train_5, y_train_pred)
print(precision)
recall = recall_score(y_train_5, y_train_pred)
print(recall)
为了能够用一个分数就能体现模型的好坏,sklearn提供了f1分数,f1分数结合了精度和召回率
# f1分数,结合了精度和召回率的值
f1 = f1_score(y_train_5, y_train_pred)
print(f1)
精度和召回率的权衡
很多时候我们会发现,鱼和熊掌不可兼得,我们不能保证在获得一个高精度的时候还有一个很高的召回率,这个时候我们需要做出取舍,在精度和召回率之后做权衡。
我们通过限制模型预测阀值,来调整精度和召回率。交叉验证模型,输出阀值,使用阀值与精度/召回率绘制图,来观察精度和召回率随机阀值的变化而变化的过程。
# 绘制精度召回率曲线
y_score = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3, method="decision_function")
precision, recall, threshold = precision_recall_curve(y_train_5, y_score)
def show_precision_recall_vs_threshold(precision, recall, threshold):
"""
显示精度召回率和阈值之间的关系
:param precision:
:param recall:
:param threshold:
:return:
"""
plt.plot(threshold, precision[:-1], "b--", label="Precision", linewidth=2)
plt.plot(threshold, recall[:-1], "g--", label="Precision", linewidth=2)
plt.legend(loc="center right", fontsize=16)
plt.xlabel("Threshold", fontsize=16)
plt.axis([-10000, 10000, 0, 1])
plt.grid(True)
# 计算精度达到90时的阈值和召回率
first_max_index = np.argmax(precision >= 0.9)
precision_90_recall = recall[first_max_index]
precision_90_threshold = threshold[first_max_index]
show_precision_recall_vs_threshold(precision, recall, threshold)
# 添加辅助线
plt.plot([precision_90_threshold, precision_90_threshold], [0., 0.9], "r:")
plt.plot([-10000, precision_90_threshold], [0.9, 0.9], "r:")
plt.plot([-10000, precision_90_threshold], [precision_90_recall, precision_90_recall], "r:")
# 添加交点
plt.plot([precision_90_threshold], [0.9], "ro")
plt.plot([precision_90_threshold], [precision_90_recall], "ro")
plt.show()

我们可以看到随着阀值的升高,精度也随之升高,但是召回率在不断下降。
下面我们再来绘制一直精度和召回率的图。
def show_recall_precision(recall, precision):
"""
绘制召回率与精度的关系
:param recall:
:param precision:
:return:
"""
plt.plot(recall, precision, "b-", linewidth=2)
plt.xlabel("Recall", fontsize=16)
plt.ylabel("Precision", fontsize=16)
plt.axis([0, 1, 0, 1])
plt.grid(True)
plt.figure(figsize=(8, 6))
show_recall_precision(recall, precision)
# 计算精度到达90时的召回率
precision_90_recall = recall[np.argmax(precision >= 0.9)]
# 绘制辅助线
plt.plot([precision_90_recall, precision_90_recall], [0, 0.9], "r:")
plt.plot([0, precision_90_recall], [0.9, 0.9], "r:")
# 绘制交点
plt.plot([precision_90_recall], [0.9], "ro")
plt.show()

我们可以看到召回率升高的同时精度在不断地下降。
ROC
除了精度召回率之外还有一种评估分类模型的指标,ROC曲线。

假正率(X轴):表示被错误分类为负类占总负类的比例。
真正率(Y轴):表示被正确分类为正类占总正类的比例,召回率的另一个称呼。
我们来绘制一个我们随机梯度下降模型的ROC曲线。
# 绘制roc曲线
def show_roc_curve(fpr, tpr, label=None):
plt.plot(fpr, tpr, linewidth=2, label=label)
plt.plot([0, 1], [0, 1], "k--")
plt.axis([0, 1, 0, 1])
plt.xlabel("FPR", fontsize=16)
plt.ylabel("TPR", fontsize=16)
plt.grid(True)
plt.figure(figsize=(8, 6))
show_roc_curve(fpr, tpr)
# 查看到精度到达90的召回率(tpr)时fpr的值为多少
fpr_precision_90 = fpr[np.argmax(tpr >= precision_90_recall)]
print(fpr_precision_90)
plt.plot([fpr_precision_90, fpr_precision_90], [0, precision_90_recall], ":r")
plt.plot([0, fpr_precision_90], [precision_90_recall, precision_90_recall], ":r")
plt.plot([fpr_precision_90], [precision_90_recall], "ro")
plt.show()
ROC曲线的另外一种表现方式就是AUC,就是ROC曲线的面积,AUC越接近1说明模型越准确。
# 查看roc曲线的auc
auc = roc_auc_score(y_train_5, y_score)
print(auc)
接下来,我们再训练一个随机森林模型然后比较两个模型的ROC曲线。
# 训练一个随机森林分类器模型
forest_fcl = RandomForestClassifier(n_estimators=100, random_state=42)
forest_fcl.fit(X_train, y_train_5)
# 交叉验证
y_proba_forest = cross_val_predict(forest_fcl, X_train, y_train_5, cv=3, method="predict_proba")
y_score_forest = y_proba_forest[:, 1]
# 绘制roc曲线
fpr_forest, tpr_forest, thresholds_forest = roc_curve(y_train_5, y_score_forest)
tpr_forest_90 = tpr_forest[np.argmax(fpr_forest >= fpr_precision_90)]
plt.figure(figsize=(8, 6))
plt.plot(fpr_forest, tpr_forest, label="RANDOM FOREST")
show_roc_curve(fpr, tpr, label="SGD")
# 绘制辅助线
plt.plot([fpr_precision_90, fpr_precision_90], [0., precision_90_recall], "r:")
plt.plot([0., fpr_precision_90], [precision_90_recall, precision_90_recall], "r:")
plt.plot([fpr_precision_90, fpr_precision_90], [0., tpr_forest_90], "r:")
plt.plot([fpr_precision_90], [precision_90_recall], "ro")
plt.plot([fpr_precision_90], [tpr_forest_90], "ro")
plt.legend(loc="lower right", fontsize=16)
plt.grid(True)
plt.axis([0, 1, 0, 1])
plt.show()
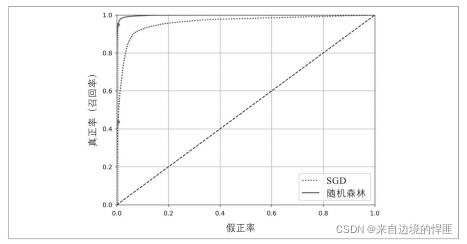
从图中我们可以看出,随机森林模型的面积要比SGD的要大,曲线更加靠经左上角,说明随机森林的模型要比SGD的性能好。我们再来看下一下随机森林模型的精度召回率以及AUC
# 计算auc、召回率和精度
auc = roc_auc_score(y_train_5, y_score_forest)
print(auc)
predict_forest = cross_val_predict(forest_fcl, X_train, y_train_5, cv=3)
print(predict_forest)
recall_forest = recall_score(y_train_5, predict_forest)
print(recall_forest)
precision_forest = precision_score(y_train_5, predict_forest)
print(precision_forest)
4、多类分类器
我们完成了二元分类器的训练,模型只能完成对是5不是5的预测,无法到达我们的预期需要识别0-9所有的数字。所以现在我们需要训练一个多类分类器SVC。
svm_clf = SVC(gamma="auto", random_state=42)
svm_clf.fit(X[:1000], y_train[:1000])
svm_predict = svm_clf.predict([one_digit])
# print(svm_predict)
svm_dec = svm_clf.decision_function([one_digit])
print(svm_dec)
print(svm_clf.classes_)
print(svm_clf.classes_[7])
对于多类分类器我们一般有两种策略来完成一种是一对剩余(是5还是其他),一对一(是5还是3),对于数据集比较小的模型,我们可以使用一对一的策略,正常的情况我们还是会使用一对剩余。
我们分别使用随机梯度下降(SGDClassifier)支持向量(SVC)随机深林(RandomForestClassifier)来训练一对剩余的模型来完成预测。
# 训练一个一对剩余的模型
ovr_clf = OneVsRestClassifier(SVC(gamma="auto", random_state=42))
ovr_clf.fit(X[:1000], y_train[:1000])
ovr_predict = ovr_clf.predict([one_digit])
print(ovr_predict)
sgd_clf = SGDClassifier(random_state=42)
sgd_clf.fit(X[:1000], y_train[:1000])
sgd_predict = sgd_clf.predict([one_digit])
print(sgd_predict)
random_forest_clf = RandomForestClassifier(random_state=42)
random_forest_clf.fit(X[:1000], y_train[:1000])
random_forest_predict = random_forest_clf.predict([one_digit])
print(random_forest_predict)
这里我们提到一个小的知识点,使用归一化来提高模型的准确性。
# 验证归一化是否能够提高准确度
sgd_score = cross_val_score(sgd_clf, X_train, y_train, cv=3, scoring="accuracy")
print(sgd_score)
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train.astype(np.float64))
sgd_scaled_score = cross_val_score(sgd_clf, X_train_scaled, y_train, cv=3)
print(sgd_scaled_score)
5、误差分析
在得到了一个多类分类之后我们需要继续使用混淆举证来对模型进行误差分析,首先我们会用自己手动的方式生成一个混淆举证,再用sklearn提供的方法绘制混淆矩阵。
sgd_clf = SGDClassifier(random_state=42)
y_train_predict = cross_val_predict(sgd_clf, X_train, y_train, cv=3)
sgd_cm = confusion_matrix(y_train, y_train_predict)
def show_confusion_matrix(matrix):
"""
手动绘制混淆矩阵
:param matrix:
:return:
"""
fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111)
cax = ax.matshow(matrix)
fig.colorbar(cax)
show_confusion_matrix(sdg_cm)
plt.show()
# sklearn绘制混淆矩阵
plt.matshow(sgd_cm, cmap=plt.cm.gray)
plt.show()

绘制出来的混淆矩阵肉眼看上去好像都还好,没有太大的误差。那是因为所有的70000张图片中0-9的数量并不是均匀分布,我们需要把混淆矩阵的值再乘以数量的占比之后再次绘制混淆矩阵。
# 计算每一类图片的数量
row_nums = sgd_cm.sum(axis=1, keepdims=True)
# 考虑每个数字的图片数量不同,考虑到数据的准确性需要对混淆矩阵的数值除以他的数量
norm_sgd_cm = sgd_cm / row_nums
# 用0填充对角线
np.fill_diagonal(norm_sgd_cm, 0)
plt.matshow(norm_sgd_cm, cmap=plt.cm.gray)
plt.show()

可以看到8这一列的颜色比较白,所以表示被预测分类为8的书两比较多,其中5是最多的。
这里不太清楚为什么书中没有继续显示8和5的图片,而是选择显示了5和3被分类的情况。
# 检查3和5的混淆
num_3, num_5 = 3, 5
X_33 = X_train[(y_train == num_3) & (y_train_predict == num_3)]
X_35 = X_train[(y_train == num_3) & (y_train_predict == num_5)]
X_53 = X_train[(y_train == num_5) & (y_train_predict == num_3)]
X_55 = X_train[(y_train == num_5) & (y_train_predict == num_5)]
# 绘制3和5的错误分类图,左上角为是正确分类为3的,右上角为错误分类为3的
# 左下角为错误分类为5的3的图片,右下角为正确分类为5的图片
plt.figure(figsize=(8, 8))
plt.subplot(221)
show_digit(X_33[:25], num_per_row=5)
plt.subplot(222)
show_digit(X_35[:25], num_per_row=5)
plt.subplot(223)
show_digit(X_53[:25], num_per_row=5)
plt.subplot(224)
show_digit(X_55[:25], num_per_row=5)
plt.show()

我们可以看确实存在了许多我们自己都无法分辨的图片,这就是我们模型预测出错的原因。
6、多标签分类
我们之前完成的都是对一个实例一个标签的预测,现在我们需要升级难度,需要完成多个标签的同时分类一个数是否是奇数,是否大于7。
训练一个K临近算法来完成这个任务,因为并不是所有的分类器都支持多标签分类。
# 多标签分类
y_train_large = (y_train >= 7)
y_train_even = (y_train % 2 == 0)
y_train_large_odd = np.c_[y_train_large, y_train_even]
# 使用K临近算法训练模型
knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train, y_train_large_odd)
knn_predict = knn_clf.predict([one_digit])
print(knn_predict)
7、多输出分类
再次加大难度,我们需要多输出,完成对一个图片的降噪功能。
添加噪音
完成添加噪音,并查看完成后的图片。
# 对图片添加噪音
noise = np.random.randint(0, 100, (len(X_train), 784))
X_train_noise = X_train + noise
noise = np.random.randint(0, 100, (len(X_test), 784))
X_test_noise = X_test + noise
y_train_noise = X_train
# 显示添加噪音和不添加噪音的区别
plt.figure(figsize=(8, 4))
plt.subplot(121)
show_img(X_test[0])
plt.subplot(122)
show_img(X_test_noise[0])
plt.show()
knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train_noise, y_train_noise)
clean_digit = knn_clf.predict([X_test_noise[0]])
show_img(clean_digit)
plt.show()
三、课后练习
1.为MNIST数据集构建一个分类器,并在测试集上达成超过97%的准确率。提示:KNeighborsClassifier对这个任务非常有效,你只需要找到合适的超参数值即可(试试对weights和n_neighbors这两个超参数进行网格搜索)。
# 构建网格参数
grid_param = [{"weights": ["uniform", "distance"], "n_neighbors": [3, 4, 5]}]
# 开始网格搜索
knn_clf = KNeighborsClassifier()
grid_cv = GridSearchCV(knn_clf, grid_param, cv=5, verbose=3)
grid_cv.fit(X_train, y_train)
print(grid_cv.best_estimator_)
print(grid_cv.best_score_)
knn_test_predict = grid_cv.predict(X_test)
knn_score = accuracy_score(y_test, knn_test_predict)
print(knn_score)
2.写一个可以将MNIST图片向任意方向(上、下、左、右)移动一个像素的功能[1]。然后对训练集中的每张图片,创建四个位移后的副本(每个方向一个),添加到训练集。最后,在这个扩展过的训练集上训练模型,测量其在测试集上的准确率。你应该能注意到,模型的表现甚至变得更好了!这种人工扩展训练集的技术称为数据增广或训练集扩展。
# 设置图片偏移
def shift_image(image, dx, dy):
image = image.reshape(28, 28)
shifted_image = shift(image, [dx, dy], cval=0)
return shifted_image.reshape([-1])
shifted_image_down = shift_image(one_digit, -5, 0)
plt.figure(figsize=(8, 4))
plt.subplot(121)
plt.title("Original", fontsize=16)
plt.imshow(one_digit.reshape(28, 28), interpolation="nearest", cmap="Greys")
plt.subplot(122)
plt.title("Shift", fontsize=16)
plt.imshow(shifted_image_down.reshape(28, 28), interpolation="nearest", cmap="Greys")
plt.show()
# 循环偏移图片
X_train_augmented = [image for image in X_train]
y_train_augmented = [image for image in y_train]
for dx, dy in [(1, 0), (-1, 0), (0, 1), (0, -1)]:
for image, label in zip(X_train, y_train):
X_train_augmented.append(shift_image(image, dx, dy))
y_train_augmented.append(label)
X_train_augmented = np.array(X_train_augmented)
y_train_augmented = np.array(y_train_augmented)
# 打乱顺序
per_index = np.random.permutation(len(X_train_augmented))
X_train_augmented = X_train_augmented[per_index]
y_train_augmented = y_train_augmented[per_index]
# 训练模型
knn_clf = KNeighborsClassifier(n_neighbors=4, weights='distance')
knn_clf.fit(X_train_augmented, y_train_augmented)
knn_augmented_predict = knn_clf.predict(X_test)
knn_augmented_score = accuracy_score(y_test, knn_augmented_predict)
print(knn_augmented_score)
3.Kaggle上非常棒的起点:处理泰坦尼克(Titanic)数据集。
泰坦尼克号文章地址
4.创建一个垃圾邮件分类器(更具挑战性的练习)
由于这里代码比较多,我把所有代码放在了git里面。
四、总结
这一章,我们完成了对MNIST的分类,从二元分类器开始,再到多类分类器、多标签分类器…一步一步的逐步递增,最后完成了对0-9数字的分类。我们在完成分类的同时还提到了一个重点,对于分类模型的性能测量。一共分为两个重点1、精度和召回率 2、ROC。
对文章有任何疑惑或者想要和博主一起学机器学习一起进步的朋友们可以添加 群号:666980220。需要机器学习实战电子版或是思维导图的也可以联系我。祝你好运!
项目地址: github

