端到端的图像压缩----《Joint Autoregressive and Hierarchical Priors for Learned Image Compression》 论文笔记

论文地址：https://arxiv.org/abs/1809.02736?context=cs.CV

代码地址：无

PixCNN 论文地址:https://arxiv.org/abs/1601.06759v3

PixCNN 代码地址：https://github.com/carpedm20/pixel-rnn-tensorflow

Minnen作品 也是一尊大神，入门必读。该文章仅供本人笔记用，如果问题欢迎讨论。

PixCNN

一 简介

最近，已经引入了层次熵模型（超先验），以作为比简单的完全分解先验算法更能开发潜伏结构的方法，从而在保持端到端优化的同时提高了压缩性能。受到概率生成模型中自回归先验的成功的启发，该文研究了自回归，分层和组合先验作为替代方案，在图像压缩的情况下权衡了它们的成本和收益。虽然众所周知，自回归模型会带来很大的计算量损失，就压缩性能而言，自回归和分层先验是互补的，并且与所有先前学习的模型相比，自回归和分层先验在潜伏中的概率结构更好。组合的模型产生了最新的速率失真性能，第一个超过了BPG传统压缩的智能压缩算法。

二 内容

2.1 创新内容

       该模型是基于Ballé 2018等人的工作.使用基于噪声的松弛来将梯度下降方法应用于方程式中的损失函数。并引入了层次化的改进熵模型。尽管先前的大多数研究使用的是（离线）的（但可能很复杂的）熵模型，但Ballé等人（2007年）。使用高斯比例混合（GSM），比例参数以超优先为条件。他们的模型可以进行端到端训练，包括联合优化超先验的量化表示，条件熵模型和基本自动编码器。关键见解是可以将压缩的超优先级作为边信息添加到生成的比特流中，从而允许解码器使用条件熵模型。以这种方式，熵模型本身是图像相关的和空间自适应的，这允许更丰富和更准确的模型。 Ballé等。表明深度神经网络的标准优化方法足以了解边信息的大小与从更精确的熵模型获得的节省之间的有用平衡。与早期的基于学习的方法相比，生成的压缩模型提供了最新的图像压缩结果。

       两种方式扩展这种基于GSM的熵模型：基线是只预测了熵模型的 $\sigma$ 参数，原文称之为（GSM）模型，而该文则通过增加预测 $\mu$ 均值的形式，该文称之为（GMM）模型，但是实际预测 $\sigma$ 和 $\mu$ 两个参数才是单高斯分布，而GMM则是预测了多高斯混合，此处模型称呼问题有出入。第二个方式： 根据生成模型的最新研究，通过自回归的模块。其余模块均与论文《Variational Image Compression With A Scale Hyperprior》中的一致。

2.2 框架细节

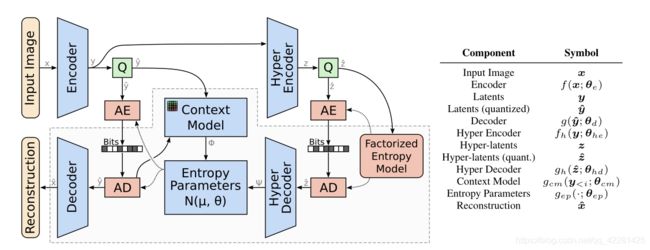
       组合模型共同优化了一个自回归组件，该组件根据其因果上下文（上下文模型）以及超优先级和底层自动编码器来预测潜伏。对实值潜像表示进行量化（$Q$），以创建潜像（$\tilde{y}$）和超潜像（$\tilde{z}$），然后使用算术编码器（AE）将其压缩为位流，并通过算术解码器（AD）对其进行解压缩。高亮区域对应于由接收机执行以从压缩比特流中恢复图像的组件。
       该自回归组件是通过一层的 $MaskConvolution$ 卷积层实现的，具体可参考论文《Pixel Recurrent Neural Networks》，通过对卷积核进行 $Mask$ 操作，掩盖了未解码点的数值，保证了自回归模型预测的当前的像素点参数仅来自于前面已经解码的点，而不取决于未解码点。

通过这种Mask 掩膜，遮蔽卷积核下面和右边的权重，这种卷积核与特征图进行卷积的时候，可以可知卷积得到的结果与“未来”的数据无关。

自回归模型的问题在于存在严格是时序关系，只能先得到前面的点才能得到当前点的信息，而前面的点也只能依靠更前面的点得到，即表现为在解码的时候，原始的解码方式具有并行性质，而自回归则是串行顺序。如下例子：
       假定有一百个待解码点 [$x_1$,$x_2$,$x_2$,$x_3$ … $x_{100}$]，基线模型地解码方式在于通过分层先验模型传输解码需要的参数信息到解码端： [(${\mu }_1,{\sigma }_1$),(${\mu }_2,{\sigma }_2$),(${\mu }_3,{\sigma }_3$) …(${\mu }_{100},{\sigma }_{100}$)]，这部分的信息解码器是无法自己生成的，所以需要传输。然后解码端根据建模的参数信息进行解码，其中重要的是，上述的的建模信息的生成是并行生成的。该论文中优化联合自回归以及分层先验的方式则是串行的，具体运作规则如下：分层先验会根据源数据[$x_1$,$x_2$,$x_2$,$x_3$ … $x_{100}$] 生成 [${\psi }_1$,${\psi }_2$,${\psi }_3$ … ${\psi }_{100}$],分层先验模型的生成方式是并行的，而自回归模块则生成[${\varphi }_1$,${\varphi }_2$,${\varphi }_3$ … ${\varphi }_{100}$], 其串行体现与，在自回归模型训练结束后，${\varphi }_1$ 的 参数值是根据$x_0$推断的，由于没有$x_0$,则初始化一个$x_0$,而${\varphi }_2$，由$x_1$已知的情况下才能得到，${\varphi }_3$，由$x_2$已知的情况下推断得到。解码顺序是：解码端通过初始化 $x_0$,然后推断得到 ${\varphi }_1$， ${\varphi }_1$与${\psi }_1$进行通道拼接操作后经过几个$1\times 1$的卷积层，得到 (${\mu }_1,{\sigma }_1$)，然后解码得到 $x_1$,得到 $x_1$可以推断得到 ${\varphi }_2$，${\varphi }_2$与${\psi }_2$进行通道拼接操作后经过几个$1\times 1$的卷积层，得到 (${\mu }_2,{\sigma }_2$)，然后解码得到 $x_2$，不断反复依次生成需要的 [(${\mu }_1,{\sigma }_1$),(${\mu }_2,{\sigma }_2$),(${\mu }_3,{\sigma }_3$) …(${\mu }_{100},{\sigma }_{100}$)]，之后得到解码的点：[$x_1$,$x_2$,$x_2$,$x_3$ … $x_{100}$]。上述过程可以看出，这种自回归形式仅仅依靠已经解码的可以推测出来（我自己推我自己），即不需要额外的码率进行传时，但是这种串行的性质，需要极大的时间复杂度。

       自回归模型和超先验模型可以进行有效的互补工作。首先，从超优先级的角度出发，我们看到对于相同的超先验网络体系结构，对熵模型的改进需要更多的辅助信息。辅助信息会增加压缩文件的总大小，从而限制了其优势。相反，将自回归分量引入先验不会引起潜在的速率损失，因为预测仅基于因果关系，即基于已经被解码的潜像。同样，从自回归模型的角度来看，我们期望一些无法完全从因果关系中消除的不确定性。但是，超先验网络可以“展望未来”，因为它是压缩比特流的一部分，并且被解码器完全了解。因此，超级优先级可以学会存储减少自回归模型中的不确定性所需的信息，同时避免存储可以从上下文中准确预测的信息。

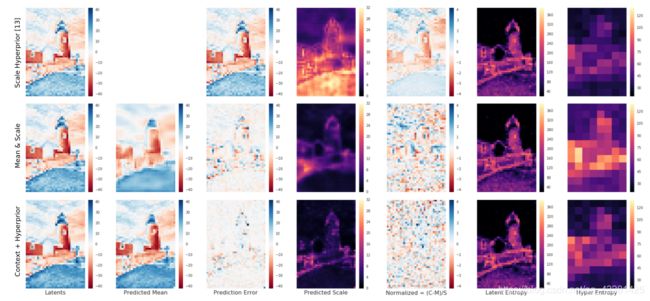
通过使用自回归模型与未使用自回归模型的结构冗余捕获可以看出，下图中，归一化后（第五张图）单超先验模型依旧存在一定的结构冗余，而联合优化自回归模型的归一化图的分布更接近与标准正太分布。

2.3 性能

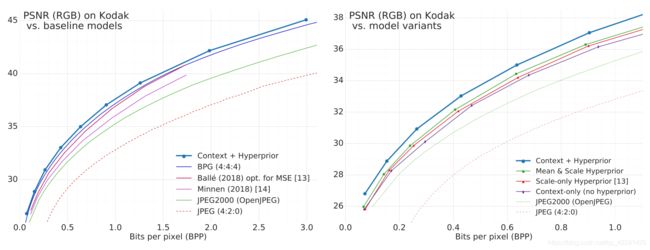
在相同码率的情况下，比BPG算法多出0.5db左右的性能提高，是第一个超过BPG的图像智能压缩算法，但是在实现速度上，编解码的时间大大增加，相对于之前的分层先验编码器，编码时间延长了近百倍。

三 总结

       实际的角度来看，自回归模型本质上是串行的，因此不如层次模型更可取，因此无法使用诸如并行化之类的技术来加速。为了报告包含自回归分量的压缩模型的性能，避免在本文中实现完整的解码器，而是比较香农熵。通过经验证明，这些测量值在算术编码生成的位流大小的百分之几以内。概率密度蒸馏已成功用于绕过语音合成任务的自回归模型的序列性质[38]，但不幸的是，由于先验和后验之间的耦合，相同类型的方法无法应用于压缩领域。算术解码器。为了解决这些计算问题，正在考虑采用其他技术来降低上下文模型和熵参数网络的计算要求，例如设计紧密的集成。具有可微自回归模型的算术解码器。未来研究的另一方向可能是通过在严格的等级先验中引入更多的复杂性来完全避免因果关系问题。