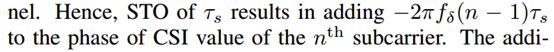SpotFi详解

注：此文档作为论文的注解，与论文配合着看最好，注解中有些次要的东西省去了，所以单看起来可能过于跳跃，一定要同时看看原文啊，另外，有些句子还是原汁原味的好，帮助理解
原文：SpotFi: Decimeter Level Localization Using WiFi

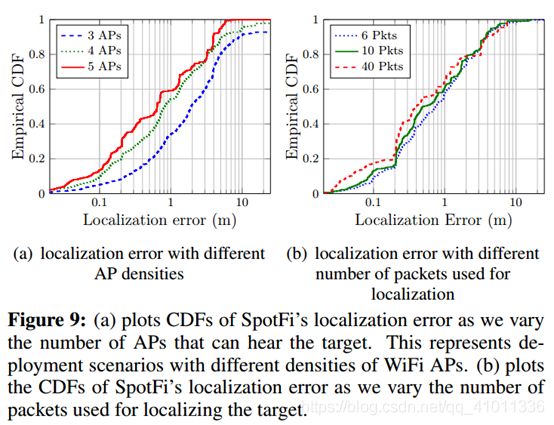
Spotfi工作分三步

1 用一个目标到达AP的信号来估计不同多径分量的AOA和TOF，通过使用商用APs的CSI信息
2估计每一个AOA和TOF对是直达路径所产生的概率
3 通过以上信息计算最有可能产生已知的观察到的RSSI和估计出的AOA的目标位置

只需要收集CSI值，时间戳，AP的MAC地址，并将其送给中央服务器，软件即可以实现
3.1用于估计AoA和ToF的SpotFi超分辨率算法
问题是，只有三根天线情况下，怎样准确估计每个多径分量的AOA
MUSIC要求天线数量多于信号源数量，说白了，关键是我们可以测量传播路径特性的传感器的数量，以及我们可以在传感器阵列上获得的独立测量的数量。
其实，传感器的数量并不由天线（intel5300只有3根天线）数量限制，事实上，wifi有很多的子载波，在他们上面我们可以得到独立的CSI测量，传感器的数量可以扩展至子载波数目和天线数的乘积，比如，intel5300上的传感器数量就是30*3=90个

同一天线的两路子载波，从第k条路径过来，TOF为Tk，则相对相移是

如时延TOF为10ns，频率间隔为40MHz，相移就是0.8pi
第k条路径，TOF为Tk，一根天线的第n个子载波相对于第一个子载波的相移为


记
具体地说，考虑由所有天线上的所有子载波组成的传感器阵列。测量矩阵X由各天线各子载波的CSI叠加而成，为单列矩阵。每个传播路径在每个传感器上都引入一个不同的相移，这取决于它的ToF和AoA

然而，在所有天线的所有子载波上叠加CSI得到的测量矩阵是一个单列单位秩矩阵。现在我们描述如何获得一个列数大于路径数的度量矩阵

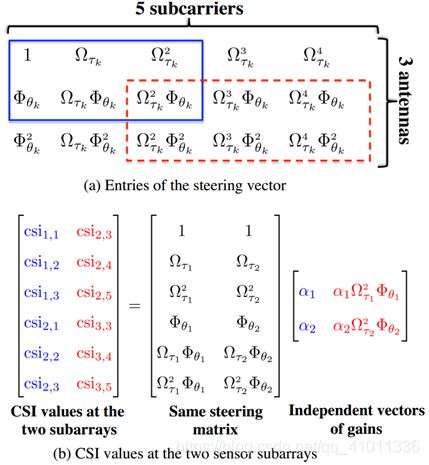
用例子说明最好，假设有两条路径，考虑图3(b)中方程左侧(LHS)矩阵两列中显示的两个传感器子阵对应的子载波上的CSI。与图3(b)第一列对应的第一传感器子阵由天线1和2上的前三个子载波组成。与图3(b)第二列相对应的第二传感器子阵由天线2和3上的子载波3至5组成。我们将在下面的段落中说明，这两个传感器子阵上的测量值可以写成相同向量的线性组合，但是增益不同，如图3(b)所示。因此，如果我们能够识别出L个这样的传感器子阵，他们的CSI值可以写成相同向量的线性组合，那么MUSIC算法就可以应用到这些子阵上CSI测量得到的测量矩阵上

为了直观理解为什么图3(b)所示的两个传感器子阵的CSI可以写成相同向量的线性组合，让我们看看图3(a)所示的求kth传播路径的Eq. 7中导向矢量的分量。

我们观察到，两个传感器子阵的相应元素之间的相移通过一个共同的尺度因子相关联。例如，第二传感器子阵左上传感器的相移，即，在天线2处的副载波3，通过乘以第一传感器子阵左上角的相移得到，即、副载波在天线1×2(τk)Φ(θk)。这个比例因子实际上是我们在这个传播路径中看到的2个子载波和1个天线的相移项，这是预期的，因为除了2个子载波和1个天线的位移，这两个传感器子阵列在结构上是相同的。常见的比例因子2(τk)Φ(θk),取决于相对两传感器子阵天线和副载波的转变以及传播路径参数,因此不同的路径是不同的。为两条路径的复增益，使用这两个复增益对相应的导向矢量进行加权，得到第一个子阵列的CSI值，对于子阵列二同样如此，只是此时增益变成
和

如图3(b)所示。因此，我们证明了这两个传感器子阵列的CSI可以写成相同向量的线性组合。此外，第二子阵的复增益向量与第一子阵的复增益向量线性无关，因为不同路径对应的衰减被不同因子相乘，得到第二子阵的修正增益。

通过对这些观测结果的归纳，可以证明通过移动固定的传感器子集得到的不同传感器子阵列的CSI值可以写成相同向量的线性组合。事实上，针对不同路径的固定传感器子集的导向矢量现在构成了导向矩阵A，通过将该导向矩阵的向量与不同权值相结合，我们得到了不同传感器子阵列上的CSI值。因此，如果我们在不同的传感器子阵列上使用CSI值构建一个测量矩阵X，这些传感器子阵列在结构上相似，但彼此之间存在偏移，我们就可以使用这个新的测量矩阵X成功地应用MUSIC算法

考虑intel5300，SpotFi考虑由前两个天线的前15个子载波组成的固定传感器子阵的不同位移所形成的传感器子阵上的CSI值来构造测量矩阵，如图4所示。我们把这个新的测量矩阵X称为光滑CSI矩阵。在这种结构中，转向矩阵A的维数为30xL，其中30行是由每个传感器子阵由2根天线上的15个子载波组合而成，L为传播路径数。矩阵F，为Lx30，30列是因为这是我们能得到的最大子阵列数（每次两根天线，15根子载波）。

在这一阶段，标准的MUSIC算法可以应用于平滑的CSI矩阵上，求出导向矢量，然后求出每个路径对应的AoA和ToF参数。由于使用平滑的CSI矩阵，SpotFi能够确保传感器的数量大于路径的数量，因此该算法现在运行得很好，因为SpotFi现在有30个传感器，而以前只有3个。

SpotFi是第一个将这些算法应用于普通WiFi部署的系统，其中APs和目标没有时间同步。这个想法是，虽然不同的WiFi卡没有时间同步，但是在一张WiFi卡上的所有收发链路都共享同一个采样时钟。因此，缺乏时间同步会导致在AP的不同天线上观测到的CSI出现相同的相移，我们将在后面的3.2.2节中对此进行描述。这种相移会破坏ToF值，但AoA值与AP和目标的无线电时间同步的情况相同。因此，联合的AoA和ToF估计算法仍然有助于提高AoA的精度，尽管AP只有三个天线，我们在第4节中进行了经验证明

识别直达路径AOA

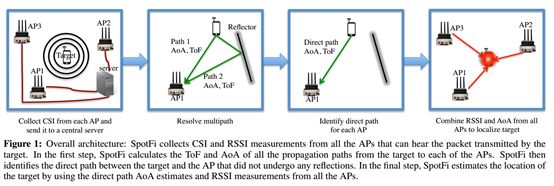
ToF估计还包括target 和AP之间采样时间偏移(STO)的延迟；除了采样时间偏移，每个WiFi收发器对之间还存在采样频率偏移(SFO)。SFO对相同的发送-接收对将采样时间偏移量从一个包更改到另一个包，从而导致对跨包的ToF估计产生附加噪声

STO为所有路径的ToF估计值添加一个常量偏移量

估计直达路径可能性

想要估计每个路径是直达路径的可能性大小，我们绘制了一个二维空间(AoA和ToF各一个)中多个测量值的AoA和ToF估计值，并应用聚类算法，直觉上，从来自同一路径的不同包中估计出的（AOA，TOF)应该聚集在一起，每一个簇的直径大小将是对应路径的（AOA，TOF）的变化方差的函数。

具体来说，我们使用了著名的高斯平均聚类算法（5个簇）来识别估计参数的聚类，集群的数量被选择为5，因为通常我们在室内环境中最多只能看到5条重要路径。聚类的均值用于估计特定传播路径的实际ToF和AoA。路径ToF的方差是通过计算属于特定路径簇的ToF估计值的总体方差来估计的，AoA也是如此。然后计算第k条路径为直达路径的可能性为

除了簇的紧密性外，似然估计还包括其他一些项。首先是与簇中点的数量相对应的术语。这里的观点是，如果一个簇对应于一个物理传播路径，那么它可能比一个伪集群有更多的度量，并且它不对应于一个底层物理路径。与平均ToF相关的术语的直觉是，直接路径的ToF最小，所以较高的ToF项应该表示较低的可能性。

SpotFi仅将其ToF估计用于似然估计，而不用于确定范围。

为了定位，spotfi寻找一个位置，在那个位置将能够使得观察到的AOA和RSSI值的方差最小，我们使用最小二乘代价测量方差，数学上，即是找到一个位置最小化以下目标函数

对不同ap的偏差进行了不同的加权，实现了一种逻辑直觉，即对直接路径AoA估计中似然度较低的ap进行惩罚，对似然度较高的ap进行奖励。由于AP上观测到的RSSI和AoA在位置坐标上是非凸的，我们不能直接应用凸优化技术来寻找目标9最小的位置。因此SpotFi采用了一种众所周知的启发式方法，即序列凸优化[72]，分段地对目标函数进行凸化，得到目标函数最小化的目标函数9

由此，SpotFi有效地过滤反射路径，准确地确定了目标的位置（算法2）

实施

与ArrayTrack及Ubicarse进行了比较

性能评估

1 SpotFi在类似于ArrayTrack和Ubicarse测试的部署中实现了0.4 m的中位定位误差

2 即使在具有挑战性的条件下，目标只有两个ap具备健壮的直接路径，SpotFi仍然表现良好，与中值定位误差为3.5 m的ArrayTrack相比，中值定位误差为1.6 m。类似地，在走廊等场景中，即使可能有多个APs，目标也不会被它们四面包围，SpotFi提供的中值误差为1.1 m，而ArrayTrack为4 m。

3 SpotFi的精度来自两个关键组件。首先是其超分辨AoA估计算法，其中值误差在LoS条件下小于5度，在NLoS条件下小于10度。在ArrayTrack实际实现中使用的MUSIC算法在相同场景下的估计误差仅为7.4和15.2度。其次，SpotFi的似然估计算法保证了在可用的估计中，可能不会选择对直接路径不正确的估计，即使选择了错误的估计，它们也会以较低的置信度加权，对位置估计的影响较小