【笔记】【机器学习基础】非负矩阵分解

非负矩阵分解

非负矩阵分解(NMF)是一种无监督学习算法，目的在于提取有用的特征，工作原理类似于PCA，可以识别出组合成数据的原始分量，也可以用于降维，通常不用于对数据进行重建或者编码。

1、将NMF应用于模拟数据

应用NMF时，我们必须保证数据是正的
两个分量的非负矩阵分解和一个分量的非负矩阵分解找到的分量

mglearn.plots.plot_nmf_illustration()

在NMF中，不存在“第一非负分量”，所有分量地位平等，减少分量个数会删除一些方向。NMF使用了随机初始化，根据随机种子的不同可能会产生不同的结果。

2、将NMF应用于人脸图像

NMF的主要参数：想要提取的分量个数。
通常这个数字要小于输入特征的个数（否则将每个像素作为单独的分量就可以解释数据）。
观察分量个数如何影响NMF重建数据的好坏

（1）利用越来越多分量的NMF重建三张人脸图像

mglearn.plots.plot_nmf_faces(X_train, X_test, image_shape)

（2）提取部分分量，观察数据

from sklearn.decomposition import NMF
nmf = NMF(n_components=15, random_state=0)
nmf.fit(X_train)
X_train_nmf = nmf.transform(X_train)
X_test_nmf = nmf.transform(X_test)

fig, axes = plt.subplots(3, 5, figsize=(15, 12),
                         subplot_kw={'xticks': (), 'yticks': ()})
for i, (component, ax) in enumerate(zip(nmf.components_, axes.ravel())):
    ax.imshow(component.reshape(image_shape))
    ax.set_title("{}. component".format(i))

（3）查看分量较大的图像

compn = 3

inds = np.argsort(X_train_nmf[:, compn])[::-1]
fig, axes = plt.subplots(2, 5, figsize=(15, 8),
                         subplot_kw={'xticks': (), 'yticks': ()})
fig.suptitle("Large component 3")
for i, (ind, ax) in enumerate(zip(inds, axes.ravel())):
    ax.imshow(X_train[ind].reshape(image_shape))

compn = 7

inds = np.argsort(X_train_nmf[:, compn])[::-1]
fig.suptitle("Large component 7")
fig, axes = plt.subplots(2, 5, figsize=(15, 8),
                         subplot_kw={'xticks': (), 'yticks': ()})
for i, (ind, ax) in enumerate(zip(inds, axes.ravel())):
    ax.imshow(X_train[ind].reshape(image_shape))

根据图可知，分量较大的都是向右看或者向左看的人脸
所以提取这样的模式适合于具有叠加结构的数据包括音频、基因表达、文本数据

举例：
假设对一个信号感兴趣，是有三个不同的信号源组成的

S = mglearn.datasets.make_signals()
plt.figure(figsize=(6, 1))
plt.plot(S, '-')
plt.xlabel("Time")
plt.ylabel("Signal")

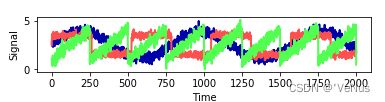
但无法观测到原始信号，这能观测到叠加混合的，需要将信号分解成原始分量。

A = np.random.RandomState(0).uniform(size=(100, 3))
X = np.dot(S, A.T)
print("Shape of measurements: {}".format(X.shape))

使用NMF还原信号：

nmf = NMF(n_components=3, random_state=42)
S_ = nmf.fit_transform(X)
print("Recovered signal shape: {}".format(S_.shape))

使用PCA进行对比：

pca = PCA(n_components=3)
H = pca.fit_transform(X)

图中显示NMF和PCA发现的信号波动

models = [X, S, S_, H]
names = ['Observations (first three measurements)',
         'True sources',
         'NMF recovered signals',
         'PCA recovered signals']

fig, axes = plt.subplots(4, figsize=(8, 4), gridspec_kw={'hspace': .5},
                         subplot_kw={'xticks': (), 'yticks': ()})

for model, name, ax in zip(models, names, axes):
    ax.set_title(name)
    ax.plot(model[:, :3], '-')

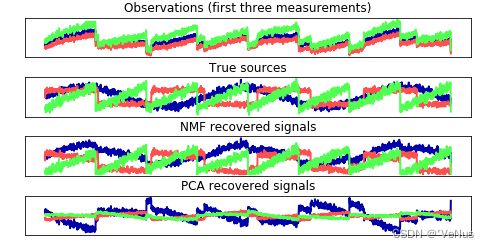
NMF在发现原始信号源时得到了不错的结果，而PCA失败了（仅使用第一个成分解释数据变化）
NMF生成的分量是没有顺序的，例子中分量顺序和原始信号完全相同（线的颜色）只是偶然