（深度学习快速入门）第二章：从线性神经网络入手深度学习（波士顿房价案例）

本节会介绍一个非常经典的案例——波士顿房价预测，该案例在机器学习中也常常提及。它代表了一种非常简单的线性回归问题，而这种线性回归问题其实就是一个只有输入和输出层的单层神经网络，所以我们可以利用这个案例来对深度学习做以初步认识

一：波士顿房价预测数据集说明

波士顿房屋于1978年开始统计，共506个数据点，数据采集了美国波士顿地区房价与周边环境因素的量化值，共有14个字段(前13个字段作输入，最后一个字段为待预测字段)，含义如下

• CRIM: 城镇人均犯罪率
• ZN: 住宅用地所占比例
• INDUS: 城镇中非住宅用地所占比例
• CHAS: 虚拟变量,用于回归分析
• NOX: 环保指数
• RM: 每栋住宅的房间数
• AGE: 1940 年以前建成的自住单位的比例
• DIS: 距离 5 个波士顿的就业中心的加权距离
• RAD: 距离高速公路的便利指数
• TAX: 每一万美元的不动产税率
• PTRATIO: 城镇中的教师学生比例
• B: 城镇中的黑人比例
• LSTAT: 地区中有多少房东属于低收入人群
• MEDV: 自住房屋房价中位数（也就是均价）

二：Pytorch搭建模型

虽然是一个很简单线性回归问题，但是这里我们还是用Pytorch像搭建其他神经网络那样来搭建这个网络模型。虽然问题很简单，但其中涉及到的一些基本元素和处理方法在其他更复杂的模型中也是一样的道理

所需库如下

import numpy as np 
import torch
from sklearn.datasets import load_boston

（1）数据处理

这一部分主要功能是对数据集做一些预处理，例如

• 数据集划分（训练集、测试集、验证集）
• 数据集归一化和标准化
• 数据增强
• …

此案例数据集数量非常少，所以这里我们只划分训练集和测试集

• X表示前13个维度作输入；y表示最后一个维度作输出。这是一个回归问题
• 前496个数据作为训练集；最后10个数据留作测试

# 读入数据
data = load_boston()
X = data.data
y = data.target

# 拆分数据
#     训练数据
X_training = X[0:496, ]
y_training= y[0:496, ]
print(np.shape(X_training))
print(np.shape(y_training))

#     测试数据
X_testing = X[496:, ]
y_testing= y[496:, ]
print(np.shape(X_testing))
print(np.shape(y_testing))

（2）网络结构

这是一个非常简单线性回归问题，只有输入和输出层，所以我们称这种网络模型为仅有单个人工神经元组成的神经网络，也即单层神经网络

• 输入层：$x_1,x_2,...,x_{13}$
• 输出层：$x_{14}$

在Pytroch中定义自己的网络时，需要继承torch.nn.Module类，并重写构造函数和forward方法

# 定义
class BostonPredictNet(torch.nn.Module):
    def __init__(self, n_feature, n_output):
        super(BostonPredictNet, self).__init__()
        self.predict = torch.nn.Linear(n_feature, n_output)
    def forward(self, x):
        out = self.predict(x)
        return out

# 初始化神经网络
net = BostonPredictNet(13, 1) # 输入为13，输出为1

（3）损失函数

X进入网络后得到的输出称之为预测值，我们总希望预测值与真实值的差距越小越好，他们的差距就称之为损失，相应构造损失的函数就为损失函数。因此，算法和模型的优化目标之一就是要让损失函数尽可能小，然后拿到此时此刻的参数。不同问题使用的损失函数也不同，具体来说

• 回归问题：一般使用均方误差作为损失函数
• 分类问题：一般使用交叉熵作为损失函数

这些损失函数在Pytorch中均有实现

# 波士顿房价问题属于回归问题，故使用均方误差作为损失函数
loss_func = torch.nn.MSELoss()

（4）优化方法

优化算法的功能是通过改善训练方式来最小化（最大化）损失函数。在神经网络训练中，梯度下降加粗样式是一个重要优化方法。梯度是一个矢量，在其方向上的方向导数最大，也就是函数在该点处沿着梯度的方向变化最快，变化率最大。所谓梯度下降，就是像一个下山的过程，下山走的每一步，都是在周围所有方向上选下降的幅度最大的

以一个简单的线性神经网络为例，其表达式为$y(x)=wx+b$，模型在训练时目的就是要得到最优的$w$和$b$，因为最优的$w$和$b$可以使损失值最小。也即优化函数为$min||y_{true}-(wx+b)|{|}^2$，对于这个优化问题我们可以使用梯度下降的方法求解，通过对$w$求导，得到梯度后，沿着梯度下降的方向对参数进行调节，直到找到最低点，此时最低点对应的值就是待求$w$

传统梯度下降执行可能会非常慢，因为在每一次更新参数之前，需要遍历整个数据集，所以我们通常会在每次需要计算更新的时候随机抽取一小批样本，这种方法叫做小批量随机梯度下降。具体来说，在每次迭代中，我们会随机抽取一小批量$\beta$（称之为批量大小(batch size)），由固定数量的训练样本组成，然后计算小批量平均损失关于模型参数的导数，最后我们将梯度乘以一个预先确定的正数$\eta$（称之为学习率(learning rate)），并从当前参数的值中减掉。这里的$\beta$和$lr$称之为超参数，需要预先指定

Pytorch在optim模块中已实现了梯度下降算法，也即优化器SGD

# 注意学习率不宜过大
optimizer = torch.optim.SGD(net.parameters(), lr=0.0001)

（5）训练预测

• 注意1：由于数据集数量太少，准确来说这里应该叫做训练验证，预测是需要使用测试集在已经训练好的模型上作预测输出的
• 注意2：和Numpy中的ndarray数组一样，Pytorch中在处理数据时使用的数据类型为张量（tensor）

训练过程如下，注意

• 一个模型一般需要训练多轮，每一轮称之为一个epoch

• 每一轮训练时包含两个步骤，首先在训练集上训练，然后在验证集上验证（这里是测试集）

  • 验证集验证当然也可以每训练10次或其他次数验证1次，没有必要每训练一次就验证一次

• 经过网络训练后得到的预测值pred是一个向量，而真实值是一个数字，所以要利用torch.squeeze(pred)降维后才能送入损失函数计算损失

• 在验证时不需要进行反向传播，也即不需要梯度信息，所以 optimizer.zero_grad()、loss_train.backward()、optimizer.step() 只在测试时出现

for i in range(1, 10000):
    
    ###################### 训练 ###############################
    
    # 前向运算
    x_data = torch.tensor(X_training, dtype=torch.float32)
    y_data = torch.tensor(y_training, dtype=torch.float32)    
    pred = net.forward(x_data)
    pred = torch.squeeze(pred)  # 降维
    # 注意损失可能过大会导致无法显示所以可以先减小，但是注意最后要复原
    loss_train = loss_func(pred, y_data) * 0.01 # 计算损失

    
    # 反向传播（三步走）
    optimizer.zero_grad() # 初始化梯度为0，也即把损失函数关于权重系数的导数置为0
    loss_train.backward() # 计算梯度
    optimizer.step() # 梯度下降，更新参数
    print("-"*30)
    print("第{}次迭代".format(i))
    print("训练集loss为{}：".format(loss_train))
    print("（训练集）预测值：", pred[0:10])
    print("（训练集）真实值：", y_data[0:10])
    
    ###################### 测试（应该叫验证） ###############################
    x_data = torch.tensor(X_testing, dtype=torch.float32)
    y_data = torch.tensor(y_testing, dtype=torch.float32)    
    pred = net.forward(x_data)
    pred = torch.squeeze(pred)
    loss_test = loss_func(pred, y_data) * 0.001 
    
    print("测试集loss为{}：".format(loss_test))
    print("（测试集）预测值：", pred)
    print("（测试集）真实值：", y_data)

训练1W次后结果如下

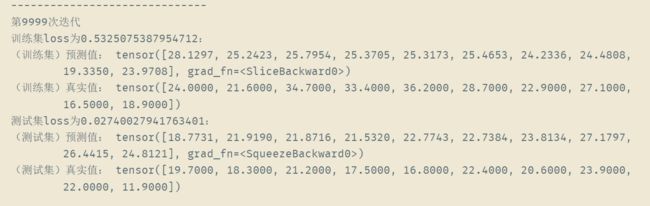
可以看出此时真实值和预测值的差距还是有点大的，这说明模型是欠拟合的，解决方法有

• 加大训练次数
• 采用大的学习率，迭代过一定次数后，动态调整学习率
• 采用其他优化函数，例如Adam（全称为Adaptive Moment Estimation，自适应矩估计是一种计算每个参数或权重的自适应学习率的方法）
• 再加入隐藏层，并使用激活函数提升非线性表达能力。代码如下

def __init__(self, n_feature, n_output):
        super(BostonPredictNet, self).__init__()
        self.hidden = torch.nn.Linear(n_feature, 100)
        self.predict = torch.nn.Linear(100, n_output)
def forward(self, x):
    out = self.hidden(x)
    # 使用非线性激活函数Relu（通用）
    out = torch.relu(out)
    out = self.predict(out)
    return out

（6）模型保存

模型训练完毕之后，需要进行保存，文件后缀名为.pth，这里保存的本质是一些参数

torch.save(net, "model/BostonPredictNet.pth")

（7）模型加载

模型保存后，就可以供其他文件加载并作预测输出了，注意

• 在加载后同时也要导入模型的定义才能继续使用
• 加载模型时，需要用map_location指定设备

new_net = torch.load("./model/BostonPredictNet.pth", map_location='cpu')