逻辑回归之sigmoid/tanh/relu激活函数

逻辑回归，就是在线性回归的基础上加入了激活函数。
常见的激活函数有：

• 1、sigmoid函数
• 2、tanh函数
• 3、relu函数

sigmoid函数

sigmoid就是一个将输出映射到[0,1]之间的函数了。函数公式

y=11+e−z y = 1 1 + e − z

图像：

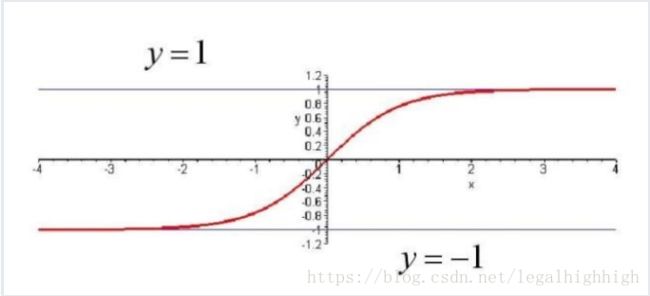
和之前计算梯度一样，我们需要的是计算loss对各个w和b的偏导数就可以了。原线性函数：

z=ωTx+b z = ω T x + b

加入激活函数后的loss:

loss=∑i=1n(yi−y^)2=∑i=12(ωTxi+b−y^)2 l o s s = ∑ i = 1 n ( y i − y ^ ) 2 = ∑ i = 1 2 ( ω T x i + b − y ^ ) 2

求偏导数的时候，需要用到复合导数计算的链式法则：

∂loss∂ω1=∂loss∂y∂y∂z∂z∂ω1 ∂ l o s s ∂ ω 1 = ∂ l o s s ∂ y ∂ y ∂ z ∂ z ∂ ω 1

∂loss∂y=2∑i=1n(yi−y^) ∂ l o s s ∂ y = 2 ∑ i = 1 n ( y i − y ^ )

∂y∂z=e−z(1+e−z)2 ∂ y ∂ z = e − z ( 1 + e − z ) 2

∂z∂ω1=x1 ∂ z ∂ ω 1 = x 1

联合起来也就是：

∂loss∂ω1=2∑i=1n(yi−y^i)e−z(1+e−z)2xi1 ∂ l o s s ∂ ω 1 = 2 ∑ i = 1 n ( y i − y ^ i ) e − z ( 1 + e − z ) 2 x i 1

这样我们发现和普通梯度函数的区别就是多了一个激活函数的梯度，也就是说逻辑回归的方法相当于在一个神经元的基础上加入了一个sigmoid的激活函数。
代码如下：

import numpy as np
import math
import time

def sigmoid(x):
    return 1.0/(1.0 + math.exp(-x))


def grad_sigmoid(x):
    return math.exp(-x)/((1+math.exp(-x))**2)

#随机梯度下降+sigmoid输出方法
sample = 100
num_input = 5

#加入训练数据
normalRand = np.random.normal(0,0.1,sample)
weight = [8,100,-1,-400,0.05]
x_train = np.random.random((sample,num_input))
y_train = np.zeros((sample,1))

for i in range(0,len(x_train)):
    total = 0
    for j in range(0,len(x_train[i])):
        total += weight[j]*x_train[i,j]
    y_train[i] = sigmoid(total + normalRand[i])

#训练

weight = np.random.random(num_input + 1)
rate = 0.01
batch = 3

def train(x_train,y_train):
    #计算loss
    global weight,rate
    predictZ = np.zeros((len(x_train),))
    predictY = np.zeros((len(x_train,)))

    for i in range(0,len(x_train)):
        predictZ[i] = np.dot(x_train[i],weight[0:num_input]) + weight[num_input]
        predictY[i] = sigmoid(predictZ[i])

    loss = 0
    for i in range(0,len(x_train)):
        loss += (predictY[i] - y_train[i])**2

    #计算梯度并更新
    for i in range(0,len(weight)-1):
        grade = 0
        for j in range(0,len(x_train)):
            grade += (predictY[j] - y_train[j])*grad_sigmoid(predictZ[j])*x_train[j,i]
        weight[i] = weight[i] - rate * grade

    grade = 0
    for j in range(0,len(x_train)):
        grade += (predictY[j] - y_train[j])
    weight[num_input] = weight[num_input] - rate * grade

    return loss

start = time.clock()
for epoch in range(0,100):
    begin = 0
    while begin < len(x_train):
        end = begin + batch
        if end > len(x_train):
            end = len(x_train)

        loss = train(x_train[begin:end],y_train[begin:end])
        begin = end
    print("epoch:%d-loss:%f"%(epoch,loss))

    if loss < 0.5:
        end = time.clock()
        print("收敛用时%s ms"%str(end - start))
        break

print(weight)

tanh函数

与sigmoid函数类似，tanh也是常见的激活函数，公式如下：

tanh(x)=ex−e−xex+e−x t a n h ( x ) = e x − e − x e x + e − x

函数求导：

tanh(x)′=1−tanh2(x) t a n h ( x ) ′ = 1 − t a n h 2 ( x )

图像：

tanh就是将输出映射到[-1,1]的范围里。

relu函数

公式：

f(u)=max(0,u) f ( u ) = m a x ( 0 , u )

图像：

relu可谓是打开了新世界的大门，2012年AlexNet碾压ImageNet时就是使用了relu作为激活函数，它的优点是梯度易于计算（不是1，就是0，只有两种），而且梯度不会像sigmoid一样在边缘处梯度接近为0（梯度消失）。