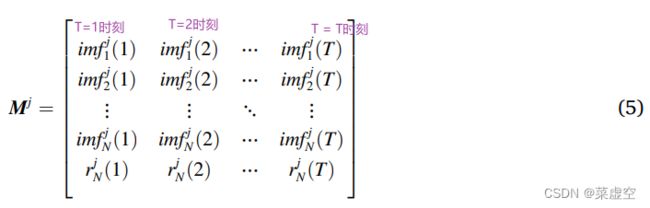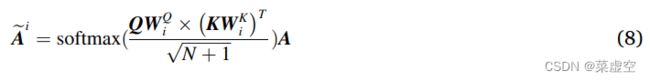基于多尺度时间特征提取的注重多元时间序列预测的图卷积网络

         多变量时间序列建模一直是一个有意义的课题。多元时间序列预测是一个基础性问题，吸引了众多研究人员的关注，然而，现有的方法大多集中在单变量预测上，很少考虑多个变量之间潜在的空间相关性。多元时间序列预测可以很自然地从图的角度来看，多元时间序列中的每个变量都可以看作是图中的一个节点，它们通过隐藏的相关性相互联系。为此，提出了一种基于多尺度时间特征提取和注意力机制的图神经网络模型，用于多元时间序列预测。具体来说，利用经验模态分解提取多元时间序列在不同时间尺度上的时域特征，形成图的节点特征。同时，采用多头注意机制构建节点之间的潜在关联，增强图中关系的合理性。此外，利用图卷积神经网络生成包含丰富空间关系的节点嵌入。最后，时间卷积网络为节点嵌入建立时间关系，实现多元时间序列预测。金融、交通、医疗等领域的实际数据验证了模型的有效性。

1.引言

近年来，随着深度学习的发展，一系列基于深度学习的时间序列预测方法被提出，如递归神经网络(RNN) (Lin et al.， 2021)、长短期记忆(LSTM) (Kong et al.， 2017)和时间卷积网络(TCN) (Bai et al.， 2018)，这些方法可以用来处理长期的时间依赖性，并可以弥补传统预测模型在非线性建模方面的不足。然而，由于真实时间序列数据存在高噪声和不确定性，深度学习模型的黑箱学习方法很难保证预测的可解释性。此外，现有的复杂系统预测方法大多基于单变量时间序列，而实际的复杂系统一般具有多元特征，例如，在一个由温度、降雨、气压等多个变量组成的系统中，任何变量的变化都会受到其他变量的影响，因此，从整体上研究具有一定相关性的多元时间序列，更有利于探索系统的本质，更适合实现多元时间序列的预测。

        多元时间序列预测可以很自然地用图来看待，多元时间序列中的每个变量都可以看作是图中的一个节点，它们通过隐藏的依赖关系相互联系。因此，利用图神经网络对多元时间序列数据建模是一种很有前途的方法，因为它可以充分利用时间序列之间的相互依赖关系，同时保持时间关系。此外，经验模态分解(EMD) (Huang et al.， 1998)作为一种处理不稳定和非线性序列的信号处理技术，用于提取不同时间尺度上的时间特征，合适的时间特征提取方法对于基于gnn的时间序列预测方法至关重要。

        本文提出了一种基于多尺度时间特征提取和注意力机制的图卷积神经网络模型。具体来说，从图的角度来看待多元时间序列的预测，从而构建一个图模型来对多元时间序列进行建模。

        ①首先，由于噪声和异常值的存在，很难直接对原始时间序列进行预测。因此,利用EMD对原始多元时间序列的每个维度序列进行特征提取，得到不同时间尺度的特征，作为后续图模型的节点特征。

        ②此外，受注意力机制的启发，采用多头注意力机制生成全连通图，探索个体变量之间的依赖关系。

        ③然后，使用GCN更新节点特性，生成节点嵌入。

        ④最后，设计TCN模块对节点嵌入的时间关系进行建模，实现多变量时间序列预测。

        本文的主要贡献如下：

        ①提出了一种基于多尺度时间特征提取和注意力机制的多元时间序列预测GCN模型，拓宽了图神经网络的应用场景。

        ②利用EMD对原始时间序列的每个维度序列进行特征提取，形成生成图的节点特征，有助于探索每个变量不同时间尺度之间的空间关系。

        ③利用一种新颖的多头注意机制来构造多个图，可以有效地构造节点之间的潜在关联，增强图中关系的合理性。

        ④利用金融、交通和医疗领域的真实数据集对模型进行了验证，最终的实验结果证明了该方法的优越性。

本文的其余部分组织如下：

第2节回顾相关工作；

第3节是预备知识；

第4节描述了所提出的方法；

第5节是实验验证；

第6节是本文的结论。

2.相关工作

2.1多变量时间预测

        目前基于深度学习的多变量时间序列预测方法大多单独对系统的单变量进行建模。因此，它们不能充分利用变量之间的潜在依赖关系。相比之下，将具有一定相关性的多元时间序列作为一个整体进行研究，更有利于探索系统的本质，从而更适合对多元时间序列进行预测。

        gnn通常假设节点的状态依赖于其邻居的状态，因此，各种gnn已被开发来捕获空间依赖性，如GCN (Kipf & Welling, 2016)， GAT (Veliˇckovi´c et al.， 2017)， STGCN (Yu et al.， 2017)等，这些在各个领域都取得了成功。

        然而，仅有少数研究者尝试将gnn应用于时间预测问题。Guo et al.(2019)提出了一种新颖的基于注意力的时空GCN模型来解决交通流预测问题，该模型可以有效应对交通流时间序列的非线性和复杂模式。

2.2时间序列领域中的图神经网络

        然而，在将gnn应用于多元时间序列预测领域时，合适的时间特征提取方法对多元时间序列预测至关重要，尤其是对于含有高噪声和不确定性的时间序列数据，这是大多数基于gnn的预测方法所忽略的，此外，这些方法不能在没有定义图的情况下对多元时间序列数据进行有效建模。
与现有的工作不同，我们在工作中使用EMD提取不同时间尺度的时间特征，可以起到数据去噪的作用。此外，还采用了多头注意机制生成多个图，可用于探索单个变量之间的依赖关系，即使没有先验图也提供了。

        上图给出了EMD分解时间序列的一个例子，从这个例子可以看出，每个IMF都是从不同的时间尺度描述原始时间序列的。从上到下分别为:原始时间序列，imf1, imf2，残差。

3.预备知识

3.1经验模态分解

EMD是Huang等人(1998)提出的一种信号处理方法，它可以自适应地将原始时间序列分解为若干个不同的本征模态函数(imf)和残差，并得到imf和残差序列具有特定的物理意义，代表了原始时间序列的不同时间尺度特征,根据Huang et al.(1998)的观点，一个信号由几个IMF和残差组成，IMF应满足以下两个条件:

        (1)在整个序列中极值点和过零点的数量必须相等或最多相差一。

        (2)在任何时候，由局部极大值定义的上包络和由局部极小值定义的下包络的平均值为零。

        对于序列x = {x1, x2，…，长度t的xT}，的过程EMD算法如下:

        (1)对序列x的局部极大值和极小值进行三次样条插值，分别得到该序列的上包络u和下包络v。

        (2)计算上下包络线的平均值，即p =(u + v) / 2。

        (3)计算x与p的差值，得到序列h。

        (4)检查h是否满足上述imf的两个条件。如果它们满足，那么结果h就是一个IMF，表示为imf。如果不是，则用h替换x，并重复上述过程，直到h满足IMF条件。

        (5)余数r是x和imf的差，用r代替x。然后步骤(1)-(4)重复N次，直到得到的第N个残差是一个单调函数。

        经EMD处理后，原始时间序列可以表示为。

式中imfi为第i个IMF, N为IMF总数 

3.2时间卷积网络

        TCN是为时间序列数据建模而设计的，在处理时间序列数据时存在两个主要的约束条件。一是不会泄露未来数据;第二，输入和输出的长度需要一致。为了实现第一个要求，TCN中使用了因果卷积，其中t时刻的输出只与t时刻及之前一层的元素进行卷积。传统的卷积通常是先进行卷积操作，然后再进行池化操作，以达到增加接收域的效果，但这会导致池化过程中一些信息丢失。而膨胀卷积不需要池化操作，通过一系列膨胀卷积逐渐扩大接收域，从而使每个卷积的输出都包含丰富的信息，用于捕获长期依赖关系。

4.本文提出的方法

        该模型主要由

        ①时间序列特征提取（EMD）

        ②图生成(Graph)

        ③节点特征更新(GCN)

        ④时间关系建立(TCN)

        四个部分组成。在时间序列分解部分，利用EMD对原始时间序列进行分解，得到不同的时间尺度特征，然后为了学习多元时间序列中变量之间的潜在关系，构建了一个图模型，将多维时间序列的每个维度作为图的一个节点，采用多头注意机制学习节点之间的关系。进一步，使用GCN更新节点特性，生成节点嵌入。最后，通过TCN建立节点嵌入的时间关系，实现多变量时间序列预测。

4.1基于EMD的时间序列特征提取

        原始时间序列经常有噪声和异常值的干扰，因此直接对原始时间序列进行预测是很困难的。因此，本文采用EMD作为特征提取方法，对原始多元时间序列进行分解。EMD得到的imf和残差序列具有特定的物理意义，代表了原始时间序列的不同时间尺度特征，可以缓解噪声的影响，有助于发现更深层次的时间关系。

        对于多元时间序列x = {x1, x2，…，xT}，其中xT∈RD表示t时刻的d维变量，t表示时间序列的长度。取第j维时间序列为例，EMD分解结果可由。

        矩阵形式的第j维时间序列的imf和残差表示为。

         进一步，利用EMD得到的每个子序列作为生成图的节点特征。 

4.2图的产生

        多元时间序列预测可以从图的角度来看待，多元时间序列中的变量可以看作是一个图中的节点。EMD得到的每个子序列描述了原始时间序列的不同时间尺度特征，因此可以用它来表征所构造图的节点，从而进一步发现多元时间序列中变量之间潜在的内在关系。具体来说，需要一个大小为k的滑动窗口，将原始时间序列分解得到的每个维度特征矩阵:M1 [T−k + 1: T]，M2[T−k + 1: T]，…，MD[T−k + 1: T]。进一步，将每个特征矩阵中同时存在的imf和残差拼接成一个新的矩阵，使得到k个矩阵，表示为v1,V2，…，Vk,分别表示k个时刻的节点特征矩阵:

（从每一个维度的M矩阵中单独拿出矩阵M的一列，构成T个时刻的矩阵）

        其中Vt∈表示第t时刻的初始节点特征矩阵，∈表示图第j个节点在第t时刻的初始特征向量。 

         为了探索多元时间序列中变量之间的空间依赖关系，受多头注意机制的启发，我们提出了以下方法来生成图的权值矩阵:

其中Q∈和K∈都等于节点特征矩阵， Ãi表示生成的第i个邻接矩阵（节点直接是否相互连通的0、1元素组成的矩阵）， 并且i∈{1，2,…， α}，其中α是多头注意力的数量。N +1是节点特征的维数；是Q和K的第i个转移矩阵,它们需要初始化α次，这增加了生成图的多样性。当已知多元时间序列的先验知识，即提供邻接矩阵A时，对已有邻接矩阵进行进一步学习，可以通过:

 

        从上面的计算过程中可以发现，学习到的邻接矩阵随着输入的变化而变化，因为多元时间序列中单个变量的相互依赖关系通常会随着时刻的变化而变化。 因此，如果邻接矩阵是固定的，那么一旦训练模型，学习到的各个变量之间的权值在推理阶段也是固定的，这样模型就会缺乏探索时间序列之间时变相关性的理想能力。此外，通过引入多头注意，可以得到一系列基于邻接矩阵Ãi的全连通图，不仅可以加强每个节点之间的连接，还有助于通过GCN利用全局信息对节点嵌入的后续更新,一般来说，构造多个图可以有效地构建节点之间的潜在关联，进一步增强图上关系的合理性。 

4.3节点特征更新

        在本节中，为了综合考虑变量之间的关系，利用GCN生成节点的嵌入。采用多头注意对所有k个时刻建立α全连通图，因此在每个时刻需要α个分支来实现节点嵌入操作。因此，对于给定时刻的第i个图，各层的计算过程如下图所示:

式中, l ={1,2，…，J}为第l层的隐矩阵， 特别地，是初始节点特征矩阵;代表第l层的权矩阵，是第l层的偏置;ρ是激活函数，本工作中使用了ReLU,Ãi的下标从不同的分支中选择全连接图。在本工作中，将GCN中隐藏层的维数设置为相同，而将输出层的输出维数设置为不同，分别记为和;以包含一个隐藏层的GCN为例:

 其中表示第一层的权值矩阵，表示第二层权值矩阵，表示第一层的隐藏矩阵，表示第二层的输出特征矩阵。

        图嵌入后，每个节点将得到不同分支的α嵌入。然后采用均值池化操作融合多分支信息，得到每个节点的唯一嵌入，t时刻的嵌入为。

where=[]T，t ={1, 2,…，k}， 表示第t时刻第j个嵌入节点。利用节点融合嵌入进一步建立时间关系，实现多元时间序列预测。 

4.4建立时间关系

        在获得包含变量之间空间关系的节点嵌入后，设计TCN模块，进一步增强模型的时间建模能力。具体地说，将同一节点不同时刻的节点嵌入输入到一个TCN模块中，然后对第j个TCN模块进行,它的输入形式是,其中元素表示第j个节点在时刻1 tok的节点嵌入。为了直观理解，下面以TCN模块为例。

        TCN模块包含多个剩余块，每个块包含两个扩张的卷积层。其中，第b块的第l层激活值用表示,l∈{1,2，…，L}，b∈{1,2，…，b}， γ表示滤波器的个数，b表示块的个数。在本工作中，滤波器的大小设置为2，因此每一层的卷积运算应用于两个时间戳，t和t−d，这样滤波器可以通过权值矩阵U=参数化，其中∈;和分别表示扩张卷积和加入时间戳t的剩余连接后的结果，定义为。

其中G∈和b∈分别表示剩余块中的权重和偏差。

        为了输出预测值，将t时刻最后一个残差块的输出连接到全连通层，输出t + 1时刻的预测结果，记为。

  

式中O、g分别为全连通层的权矩阵和偏置项。σ表示sigmoid函数，用σ作为激活函数。将D TCN模块输出后，可以得到多元时间序列下一时刻的预测值为：

         

4.5该方法的学习过程

         为了对多元时间序列数据进行建模并同时学习潜在的空间结构，采用了多头注意力、GCN和
TCN模块在一个端到端框架中共同学习。由于所有参数都可以通过梯度下降学习，因此均方误差作为目标函数，定义为。 

式中和分别表示第t时刻数据的第j维真值和预测值。 

5.实验结果

        在本节中，首先介绍数据集描述和实验设置。然后，使用来自金融、交通和医疗领域的真实数据集，用各种基准模型验证所提出的方法。并通过烧蚀实验分析了各成分对模型的影响。最后，对超参数进行了讨论。

5.1数据集描述

(a)台湾证券交易所
TAIEX(资本化加权股票指数)数据集包含2000 - 2004年5年台湾股票指数的每日价格，可通过雅虎财经(https://finance.yahoo.com)获取。

(b) Traffic数据集包含2016年4月1日- 30日北京市6条道路分钟级交通速度数据，获取路径为(https://github.com/BuaaPercy/Traffic-DataSet-of-Beiji ng-Road)。

(c)匈牙利水痘病例数据集包含县级时间序列，其中描述了匈牙利医生每周报告的水痘病例数。CCH数据集在2005年1月至2015年1月期间每周收集，可从(Rozemberczki等人，2021年)获得。

        所有数据集分为训练集、验证集和测试集，其中训练集用于模型训练，验证集用于模型选择，测试集用于模型测试。具体数据集划分如表2所示。 

5.2实验步骤

 1.首先，在将数据输入到模型，与大多数时间序列预测方法相同，采用最大最小归一化方法将数据归一化到[0,1]范围内。

        归一化公式如下:

        和分别为原始值和归一化值; 

        和分别表示原始序列中的最大值最小值；

        归一化后，时间序列可以由[]变换为[],本文中， = 0, = 1

2.随后，利用EMD对归一化时间序列进行分解。 

        此外，将数据库分为训练集、有效集和测试集，训练集用于建模训练，有效集用于选择最佳模型，测试集用于模型评价。最后，对预测结果进行了重整，并计算了评价指标。

        以下指标用于评估模型的性能，包括均方根误差(RMSE)，均方误差(MSE)和平均绝对误差(MAE)，其中RMSE、MSE和MAE由下列方程定义:

式中，和分别为序列中t时刻的原始值和预测值。 

         如前所述，EMD是一种自适应时间序列处理技术，这意味着不需要手动设置imf的数量。但由于每个维度序列分解出的imf个数可能不同，因此将其设为一个固定值，其大小取决于分解得到的imf个数最小的序列。经验地将TCN模块的超参数设置为在所有数据集中一致。其中，滤波器大小设为2，分块数设为3，每个分块包含两个卷积层，每个分块对应的扩张为1、2、4。此外，还有三个超参数可能会影响模型的性能，分别是滑动窗口的大小k、GCN 的隐藏维数和GCN 的输出维数。

        因此，为了选择最优组合，对每个数据集进行网格搜索，其中k的范围为[2,12]，hhidden和houtput的范围为[2,6]。每个数据集上超参数的最佳组合如表3所示。进一步超参数讨论将在第5.7节中提供。

5.3TAIEX数据集的案例研究

        在本节中，为了验证所提出的模型对于多输入单输出问题的效能，本节使用台北加权指数数据集，其中包括2001至2004年四年台湾股票指数的每日数据。具体来说，利用开盘价、高位、低位和收盘价数据来预测第二天的开盘价。与其他比较方法一样，每年数据的前10个月用于模型训练和参数优化，最后2个月用于测试。所提出的模型和常规时间序列预测方法对四年数据的均方根误差(rmse)显示在表4。

5.4Traffic数据集的案例研究

5.5CCH数据集的案例研究

5.6消融实验

5.7超参数分析

6.结论