9.异常检测,高斯分布,极大似然估计
1. 基本介绍
异常是相对于其他观测数据而言有明显偏离的,以至于怀疑它与正常点不属于同一个数据分布。
异常检测是一种用于识别不符合预期行为的异常模式的技术,又称之为异常值检测。识别如信用卡欺诈,工业生产异常,网络流里的异常(网络侵入)等问题,针对的是少数的事件。
- 异常在整个数据集中发生频率是很小的
- 异常数据的特征显著区别于正常数据
对于异常点,目前有三种比较公认的分类方式:
- 单点异常:也可以称为全局异常,即某个点与全局大多数点都不一样,那么这个点构成了单点异常。
- 上下文异常(Contextual Outliers):这类异常多为时间序列数据中的异常,即某个时间点的表现与前后时间段内存在较大的差异,那么该异常为一个上下文异常点。
- 集体异常(Collective Outliers):这类异常是由多个对象组合构成的,即单独看某个个体可能并不存在异常,但这些个体同时出现,则构成了一种异常。
异常检测主要分为两类:
①数据有标签,对于这样的数据,我们期望训练一个分类器,这个分类器除了要能告知正常数据的类别外,还要对于异常数据输出其属于“unknown”一类,这个任务叫做Open-set Recognition;
②数据无标签,这类数据分为两种,一种是数据是干净的(clean),也就是说数据集中不包含异常数据,另一种是数据是受污染的(polluted),数据集中包含少量的异常数据。受污染的数据是更常见的情况。
2. 高斯分布
高斯分布(Gaussian Distribution)又称正态分布(Normal Distribution)。
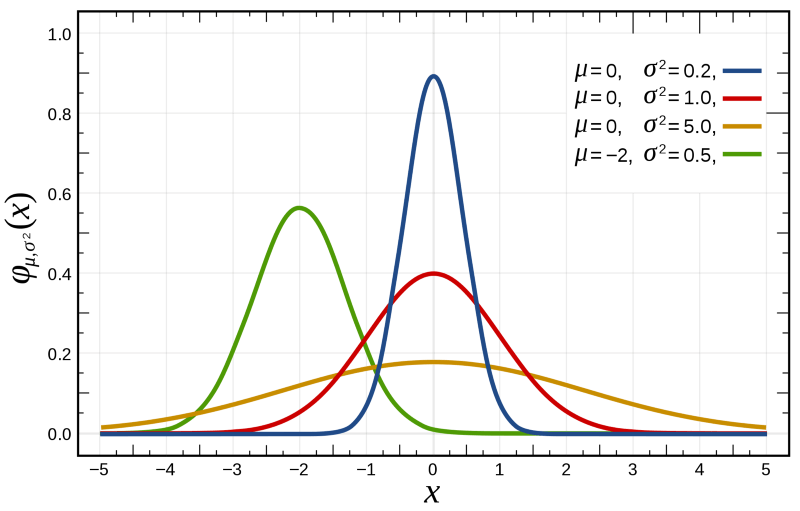
若随机变量X服从一个数学期望为μ,方差为 σ2 的正态分布,则应记为 X∼N(μ,σ)。高斯分布的概率密度函数为正态分布,期望值μ决定了其位置,其标准差σ决定了分布的幅度。当μ=0,标准差σ=1时的正态分布是标准正态分布。高斯分布的公式如下所示:
f ( x ) = 1 σ 2 π e − ( x − μ ) 2 2 σ 2 f(x)=\frac{1}{\sigma \sqrt{2 \pi}} e^{-\frac{(x-\mu)^{2}}{2 \sigma^{2}}} f(x)=σ2π1e−2σ2(x−μ)2
对于任意高纬度的正太分布,其中 x∈R^n,Σ 为协方差矩阵,它的概率密度函数为:
f ( x ) = 1 ( 2 π ) h ∣ Σ ∣ e − 1 2 ( x − μ ) T Σ − 1 ( x − μ ) f(x)=\frac{1}{\sqrt{(2 \pi)^{h}|\Sigma|}} e^{-\frac{1}{2}(x-\mu)^{T} \Sigma^{-1}(x-\mu)} f(x)=(2π)h∣Σ∣1e−21(x−μ)TΣ−1(x−μ)
高斯分布的常用性质:
- 两组服从高斯分布的数据相加仍满足高斯分布
- 两组服从高斯分布的数据相乘仍满足高斯分布
3. 极大似然估计
极大似然估计,通俗理解来说,**就是利用已知的样本结果信息,反推最具有可能(最大概率)导致这些样本结果出现的模型参数值!**极大似然估计提供了一种给定观察数据来评估模型参数的方法,即:模型已定,参数未知。
极大似然估计需要满足这样一个假设:所有的采样都是独立同分布的!而且训练样本的分布能代表样本的真实分布。
对于正态分布数据或者近似满足正态分布的数据,我们可以通过极大似然估计,得到模型中 μ 和 σ 的值,那么我们就近似认为这个模型的均值和方差就是我们计算出来的数据。
由于样本集中的样本都是独立同分布,可以只考虑一类样本集D,来估计参数向量θ。记已知的样本集为:
D = { x 1 , x 2 , ⋯ , x N } D=\left\{x_{1}, x_{2}, \cdots, x_{N}\right\} D={x1,x2,⋯,xN}
似然函数(linkehood function):联合概率密度函数P(D|θ)称为相对于数据集的 θ 的似然函数。如下公式:
l ( θ ) = p ( D ∣ θ ) = p ( x 1 , x 2 , ⋯ , x N ∣ θ ) = ∏ i = 1 N p ( x i ∣ θ ) l(\theta)=p(D \mid \theta)=p\left(x_{1}, x_{2}, \cdots, x_{N} \mid \theta\right)=\prod_{i=1}^{N} p\left(x_{i} \mid \theta\right) l(θ)=p(D∣θ)=p(x1,x2,⋯,xN∣θ)=i=1∏Np(xi∣θ)
如果Θ是参数空间中使得似然函数最大的θ值,那么他就是最可能的参数值,也就是所谓的极大似然估计值。这个最可能值通常需要通过取对数、求导,进一步求解,此处不再赘述。
对于正态分布而言,进行一系列推导以后,得到极大似然估计为:
{ μ ∗ = x ˉ = 1 n ∑ i = 1 n x i σ ∗ 2 = 1 n ∑ i = 1 n ( x i − x ˉ ) 2 \left\{\begin{array}{l} \mu^{*}=\bar{x}=\frac{1}{n} \sum_{i=1}^{n} x_{i} \\ \sigma^{* 2}=\frac{1}{n} \sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2} \end{array}\right. {μ∗=xˉ=n1∑i=1nxiσ∗2=n1∑i=1n(xi−xˉ)2
极大似然估计方法的特点:
- 比一般的估计方法更加简单
- 收敛性:无偏或者渐近无偏,当样本数目增加时,收敛性质会更好
- 如果假设的类条件概率模型正确,则通常能获得较好的结果。但如果假设模型出现偏差,将导致非常差的估计结果。
4. 算法设计
了解基础原理以后,来看一下通过高斯分布开发异常检测算法的步骤。
首先,对于给定的数据集,我们要针对每一个特征计算它的μ和σ;
一旦获得了平均值和方差的估计值,给定新的一个训练实例,根据模型计算p(x)
p ( x ) = ∏ j = 1 n p ( x j ; μ j , σ j 2 ) = ∏ j = 1 1 1 2 π σ j exp ( − ( x j − μ j ) 2 2 σ j 2 ) p(x)=\prod_{j=1}^{n} p\left(x_{j} ; \mu_{j}, \sigma_{j}^{2}\right)=\prod_{j=1}^{1} \frac{1}{\sqrt{2 \pi} \sigma_{j}} \exp \left(-\frac{\left(x_{j}-\mu_{j}\right)^{2}}{2 \sigma_{j}^{2}}\right) p(x)=j=1∏np(xj;μj,σj2)=j=1∏12πσj1exp(−2σj2(xj−μj)2)
计算出该概率以后,我们根据已经设置好的阈值来判断数据是否异常。
if p ( x ) { < ε anomaly > = ε normal \text { if } p(x)\left\{\begin{array}{ll}<\varepsilon & \text { anomaly } \\>=\varepsilon & \text { normal }\end{array}\right. if p(x){<ε>=ε anomaly normal
为了保证算法的鲁棒性,我们有必要进行评价和优化:
(1)根据测试集数据,通过极大似然估计方法构建p(x)函数
(2)对交叉检验集,我们尝试使用不同的值作为阀值,并预测数据是否异常,根据 F1值或者查准率与查全率的比例来选择
(3)选出 后,针对测试集进行预测,计算异常检验系统的1值,或者查准率与查全率之比
另外,由于一般数据中异常数据所占比例很小很小,所以数据的划分也十分需要技巧。
例如:我们有 10000 台正常引擎的数据,有 20 台异常引擎的数据。 我们这样分配数据:
训练集:6000台正常引擎的数据
交叉验证集:2000台正常引擎和10台异常引擎
测试集:2000台正常引擎和10台异常引擎
5. 对比监督学习
| 异常检测 | 监督学习 |
|---|---|
| 非常少的正向类(异常数据y=1),大量的负向类 | 同时有大量的正向类和负向类 |
| 存在许多不同种类的异常,非常难 | 有足够多的正向类实例,足够用于训练 |
| 未来遇到的异常可能与已有数据差异很多 | 捕获的异常非常近似与现有正向类实例 |
当正样本的数量很少,甚至有时候是0,即出现了太多没见过的不同的异常类型,对于这些问题,通常应该使用的算法就是异常检测算法。
异常检测算法是基于高斯分布的。当然不满足高斯分布也能处理,但是最好转成高斯分布。误差分析是特征选择中很重要的点。
有些异常数据可能出现较高的p(x)的值,被算法当做是正常数据。通过误差分析,增加新的特征得到新的算法,帮助我们更好地进行异常检测。