Invertible Image Rescaling 可逆图像缩放:完美恢复降采样后的高清图片(ECCV 2020 Oral )
论文地址:https://arxiv.org/pdf/2005.05650.pdf
开源代码:https://github.com/pkuxmq/Invertible-Image-Rescaling(即将开源)
研究背景
不知道同学们平日里上网有没有遇到过这种情况:自己精心拍摄的高清照片/视频,想发给朋友or分享到朋友圈/微博/抖音/知乎,结果上传文件之后,直接被无良服务器压成超低分辨率渣画质。甚至有些图片/表情包在经过多次传播之后,画质已经糊到惨不忍睹。
其实,图片的降采样(缩放)可以说是对数字图像最常见的操作了,它的用处多种多样:压缩图片尺寸、节省服务器存储or带宽、适配不同分辨率的屏幕等等。像现在服务器资源这么贵,大家发微博/知乎也不交钱,顶多给各位多塞点广告,所以高清图片和视频自然是能压则压,能分得清张一山和夏雨就可以了。
如何恢复降采样后的图片是图像处理中一个非常有挑战的问题,一直没有被很好的解决。
我们这篇最新工作,就巧妙地尝试从本质上解决这个问题,论文已被ECCV2020收录为Oral 论文。
2
方法
对降采样后图片的原图求解是一个典型的病态(ill-posed)问题:
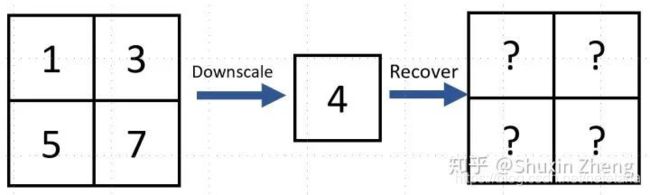
现在有一张图片有4个像素,值分别为1,3,5,7。假设对原图进行双线性插值降采样(Bilinear Interpolation),得到像素值为4的低分辨率图片。那么,如何从这一个像素还原出原图呢?
这个问题太难了,有太多种4个像素取值的组合都可以得到同样一张低分辨率图片。如果是4x降采样,则会有16个像素被采样成一个点。。想要精确地从一个像素还原出原图?你看看那些像素上的"?"眼熟不。。。
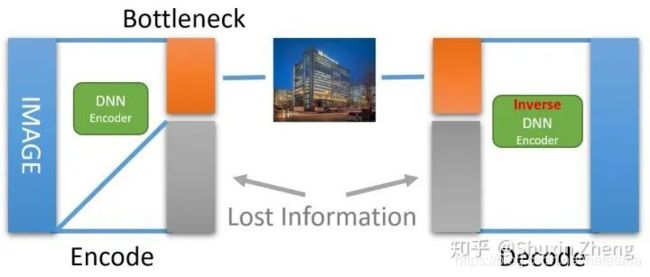
为什么这是一个病态问题?这是因为在降采样的过程中存在着信息的丢失(information loss), 以至于无法很好地还原回原图。而前人的做法一般是使用一个超分辨率的卷积神经网络,尝试从大量的数据中强行学习低分辨率到高分辨率的映射关系;或者使用encoder网络对原图进行降采样,同时使用decoder网络还原图片,二者进行联合训练(jointly training)达到更好的效果。但以上这些方法都没有从本质上解决病态问题,效果也不尽如人意。因此我们需要更聪明的方法来解决病态问题。
基于DNN的Encoder-Decoder结构对图像进行缩放和还原
刚才提到了病态问题的产生是由于信息的丢失,那么具体是什么信息被丢失了呢?
“High-frequency content will get lost during sample rate conversion.” --Nyquist-Shannon Sampling Theorem
正是由于高频信息的丢失导致了我们无法很好的还原高清原图,那么如果我们“保留”这些高频信息呢?
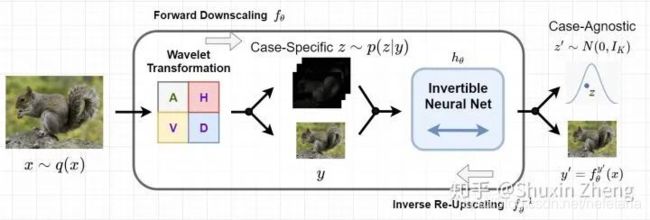
为了可以显式地保留高频信息,我们将降采样的过程替换为小波变换:由小波变换我们可以得到原图的一个低频分量和三个不同方向的高频分量。这里的低频分量与双线性插值降采样得到的低分辨率结果是一样的,而高频分量则是在降采样过程中被丢失的信息。
当我们选择保留全部信息时,我们可以使用小波变换的逆变换(即反函数,如果
![]()
,那么
![]()
),很轻松地将原图恢复出来。同理,对于使用DNN进行降采样的图片,我们如果保留了全部信息,那么也可以使用DNN的反函数将原图恢复回来。
对于深度学习模型这样一种复杂的非线性函数,它的反函数是什么呢?这里我们要用到可逆神经网络(Invertible NN, INN)模型。对可逆神经网络模型不熟悉的同学,推荐阅读Lilian Weng的博客:Flow-based Generative Model. 我们采用了最简单的Normalizing Flow的形式。这里需要注意,flow-based模型是严格可逆的。从另一个角度来思考这个问题,降采样和升采样本来就是一对逆任务,是否便应当使用可逆神经网络?
有了可逆神经网络模型,我们可以把之前的Encoder-Decoder网络换成INN和它的反函数,这样,如果我们可以保留全部信息,就能完美地恢复出原始高清图片。然而,我们显然无法在存储、传输低分辨率图片时还附带这些本应被丢失的信息(低分辨率图片的维度+丢失信息的维度=原始图片的维度),而丢弃这些信息又让我们无法使用INN来恢复出原图。所以,折腾了半天又把这条路堵死了?
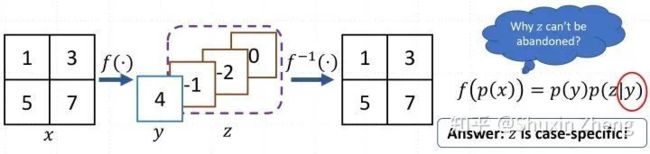
别急,我们再来回顾一下前面的简单例子:
我们令x表示原始高清图片,y和z分别表示低频与高频分量。小波变换![]() 将p(x)转换为
将p(x)转换为![]() 。z本该被丢弃,然而却无法被丢弃(丢弃后无法通过
。z本该被丢弃,然而却无法被丢弃(丢弃后无法通过![]() 恢复x),其原因在于z的分布是condition on y,即z
恢复x),其原因在于z的分布是condition on y,即z
是与样本相关的(case-specific),因此分布![]() 是难以获知的。那我们的insight就是:只要捕捉到丢失信息(Lost Information)的分布,就能得到关于它最多的信息。因此如果能令z与y相互独立,并且使所有的z(over dataset)通过某个变换服从一个预定的简单分布(如高斯分布),那么就可以被安全地丢弃,需要它时再采样就好了。
是难以获知的。那我们的insight就是:只要捕捉到丢失信息(Lost Information)的分布,就能得到关于它最多的信息。因此如果能令z与y相互独立,并且使所有的z(over dataset)通过某个变换服从一个预定的简单分布(如高斯分布),那么就可以被安全地丢弃,需要它时再采样就好了。
此时,轮到我们的INN出场了。我们引入变量![]() ,令
,令![]() 。
。![]() 是一个INN,负责把
是一个INN,负责把![]() 转换为
转换为![]() (这步有定理保证[1])。此使
(这步有定理保证[1])。此使![]() 的分布已经与y无关了,即case-agnoistic。同时,INN还可以生成符合我们要求的(如视觉效果更好的/便于压缩的..)。
的分布已经与y无关了,即case-agnoistic。同时,INN还可以生成符合我们要求的(如视觉效果更好的/便于压缩的..)。
对于case-agnoistic的![]() ,我们可以放心地将其丢弃;而当需要恢复原图时,我们可以在高斯分布中进行采样来得到
,我们可以放心地将其丢弃;而当需要恢复原图时,我们可以在高斯分布中进行采样来得到![]() 。这里需要注意,整个过程并不是完全没有信息丢失,这是因为我们使用了一个分布(高斯分布)中的一次随机采样来代替符合该分布中的一个特定样本点。但是由于我们的INN已经学习到如何将符合高斯分布的点(结合
。这里需要注意,整个过程并不是完全没有信息丢失,这是因为我们使用了一个分布(高斯分布)中的一次随机采样来代替符合该分布中的一个特定样本点。但是由于我们的INN已经学习到如何将符合高斯分布的点(结合![]() )恢复为case-specific的
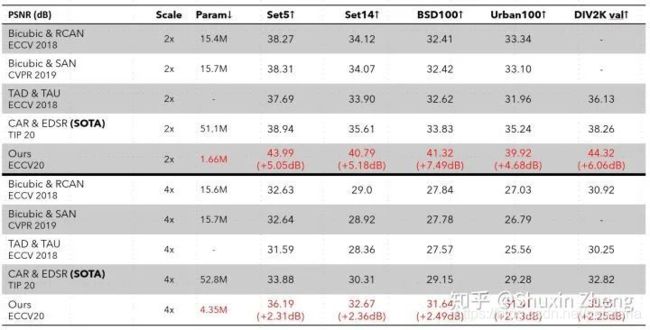
)恢复为case-specific的![]() ,因此相对于前人完全忽视ill-posed问题的做法,可以从本质上缓解求解ill-posed问题带来的困难,效果上的提升也是非常显著:
,因此相对于前人完全忽视ill-posed问题的做法,可以从本质上缓解求解ill-posed问题带来的困难,效果上的提升也是非常显著:
除了性能的大幅提升,更重要的是,得益于建模方法尝试直接解决任务的本质问题,模型所需参数量只需前人方法的1/10~1/30。下面是效果的可视化,请注意绿色框中对原图的还原程度。
更多的细节可以参考论文,包括具体的训练方法、不同采样的![]() 、如何影响图片还原、对于Out of Distribution的
、如何影响图片还原、对于Out of Distribution的![]() 模型又会有怎样的效果等等。
模型又会有怎样的效果等等。
3
总结
最后总结一下:其实Image Rescaling任务是一个很有挑战、同时在实际场景中应用广泛且商业价值巨大的任务。本文使用可逆神经网络对解决这一对逆任务进行了初步的尝试,沿着这条思路仍有很多值得发掘的点。同时,信息丢失(Information Loss)所导致的ill-posed问题在现实中也大量存在,本文提供的对Lost Information进行建模的视角,相信可以对类似任务有一定的参考价值。
参考资料:
^Nonlinear independent component analysis: Existence and uniqueness results. https://www.sciencedirect.com/science/article/abs/pii/S0893608098001403