数字图像处理合集——图像特征与理解
实现:
1、掌握图像的基本特征算法,理解图像中目标的几何特征、形状特征的物理与几何意义,并能够将特征的数学语言转换成程序描述。
2、掌握图像的角点特征算法,理解Moravec角点的物理与几何意义,并能够将角点的数学语言转换成程序描述。
3、掌握图像的纹理分析算法,理解对比度、熵、角二阶矩等纹理测度的几何意义,并能够将纹理特征描述的数学语言转换成程序描述。
1、掌握图像的基本特征算法,理解图像中目标的几何特征、形状特征的物理与几何意义。
图像的基本特征提取对研究工作有着重要的帮助,而图像的几何特征和形状特征更是尤为重要。本次实验我先将图像进行滤波处理,使用的是中值滤波。然后使用canny算子进行图像边界轮廓的提取,由于opencv有大量的接口函数可供我们使用,故我调用了许多接口函数直接画出最小外接矩和外接圆,并使用接口函数计算图像的面积、周长等,最后通过简单的数学公式运算得出外接圆半径、外接圆心坐标、矩形度延长度、周长比、似圆度、形状复杂性、一阶矩、二阶矩等图像几何特征。主要实现代码如下所示:
int features()
{
stroage = cvCreateMemStorage();
Mat src = imread("..//feature1.png");
Mat I;
imshow("原图", src);
medianBlur(src, I, 3); //中值滤波
cvtColor(I, I, CV_BGR2GRAY); //函数是一个颜色空间转换函数, 可以实现RGB颜色向HSV, HSI等颜色空间转换
Mat contours;
Canny(I, contours, 100, 255); //边缘检测算子
threshold(contours, contours, 100, 255, CV_THRESH_TRUNC); //二值化
int numcontours = cvFindContours(&(CvMat)contours, stroage, &seq, sizeof(CvContour), CV_RETR_LIST); //轮廓提取
CvMoments moments; //申请内存
CvHuMoments hu; //hu矩
cvMoments(&(CvMat)I, &moments, 0);
cvGetHuMoments(&moments, &hu);
if (ku != numcontours)
{
ku = numcontours;
printf("contournum:::: %d \n", numcontours);
}
CvSeq *c = 0;
int zz = 0;
int totl = 0;
cvSet(contourimage, cvScalar(255, 0, 255)); //cvscalar是opencv常用的结构体
cvSet(contourimage, cvScalar(125, 0, 125));
CvPoint2D32f center; //二维坐标下的点,类型为浮点
float radius;
CvPoint2D32f rectpoint[4];
CvContour *testcontour = 0; //发展自序列
//c为轮廓顶点数组
for (c = seq; c != NULL; c = c->h_next)
{
// 取得轮廓面积
double testdbArea = fabs(cvContourArea(c, CV_WHOLE_SEQ));
//取得轮廓长度
double testdbLength = cvArcLength(c);
c->block_max;
if (testdbArea >= 50 && testdbLength <= 5000)
{
//点集的最外面(up-right)矩形边界
CvRect testrect = cvBoundingRect(c); //计算点集的最外面(up-right)矩形边界
//轮廓最小外界矩形
CvBox2D testbox = cvMinAreaRect2(c); //函数能够得到轮廓的最小外接矩形 cvRectangle(&(CvMat)contours, cvPoint(testrect.x, testrect.y + testrect.height), cvPoint(testrect.x + testrect.width, testrect.y), cvScalar(255, 0, 255), 1);
//绘制简单、指定粗细或者带填充的矩形
double width = testrect.width;
double height = testrect.height;
double juxingmianji = width * height;
//找外接圆
cvMinEnclosingCircle(c, ¢er, &radius);
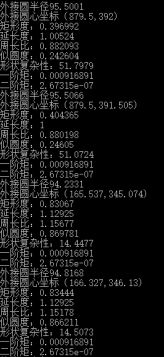
cout <<"外接圆半径"<< radius << endl;
cout << "外接圆心坐标(" << center.x << "," << center.y << ")"<<endl;
//画外接圆
cvCircle(&(CvMat)contours, cvPointFrom32f(center), (int)radius, cvScalar(255, 0, 255), 2);
//特征1矩形度
float mianjibi = testdbArea / juxingmianji;
//特征2延长度
float changkuanbi = width / height;
//特征3周长比
float zhouchangbi = 2 * (height + width) / testdbLength;
//特征4似圆度
float r = 4 * pi*testdbArea / (testdbLength*testdbLength);
//特征5形状复杂性
float e = (testdbLength*testdbLength) / testdbArea;
//不动点特征 hu.hu1 hu.hu2
cout << "矩形度:" << mianjibi << endl;
cout << "延长度:" << changkuanbi << endl;
cout << "周长比:" << zhouchangbi << endl;
cout << "似圆度:" << r << endl;
cout << "形状复杂性:" << e << endl;
cout << "一阶矩:" << hu.hu1 << endl;
cout << "二阶矩:" << hu.hu2 << endl;
}
}
namedWindow("结果图像");
imshow("结果图像", contours);
waitKey();
return 0;
}
实现效果:
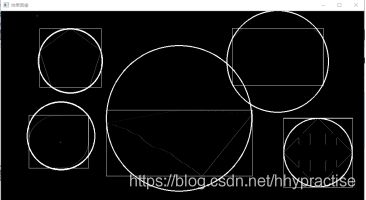
1、图像中目标的几何特征、形状特征的实验结果如图1-图3所示。
基本特征测试原图:

最小外接矩形和外接圆:
基本特征计算:
2、掌握图像的角点特征算法,理解Moravec角点的物理与几何意义,并能够将角点的数学语言转换成程序描述。
在第五次实验中我使用多次腐蚀膨胀的方法获取到图像的角点特征,本次实验采用Moravec算子进行角点特征提取。
Moravec算子通过滑动二值矩形窗口寻找灰度变化的局部最大值;其主要过程分为四步,分别是计算图像中各像素的兴趣值,给定一个经验阈值,将兴趣值大于该阈值的像素作为候选角点。选择阈值的原则:候选角点中要包含足够多的真实,局部非极大值抑制选取角点,即在一定大小的窗口中,将候选角点中兴趣值最大的作为角点,如果两个角点之间的距离过短,那么去掉其中一个角点。Moravec算子的优点是计算速度快,缺点是对图像边缘和噪声敏感,并且有方向上的局限性。主要实现代码如下所示:
void Moravec(Mat * src, int kenal, float threshold, vector<Point>*cor_point)
{
int half_kenal = kenal / 2;
float min_value;
Mat dst(src->size(), CV_8UC1, Scalar(0));
//定义Mat的格式方法:Mat a(行,列,类型,值);
// Mat a.creat(行,列,类型);
for (int y = half_kenal; y < src->rows - half_kenal; y++)
{
for (int x = half_kenal; x < src->cols - half_kenal; x++)
{
float move_value[4] = { { 0 } };
for (int win = -half_kenal; win < half_kenal; win++)
{
//0°方向方差
move_value[0] += powf(get_pix(src, x + win, y) - get_pix(src, x + win + 1, y), 2);
//45°方向方差
move_value[1] += powf(get_pix(src, x + win, y + win) - get_pix(src, x + win + 1, y + win + 1), 2);
move_value[2] += pow(get_pix(src, x, y + win) - get_pix(src, x, y + win + 1), 2);//90°方向变化量
move_value[3] += pow(get_pix(src, x - win, y + win) - get_pix(src, x - win - 1, y + win + 1), 2);
}
min_value = move_value[0];
for (int i = 0; i < 4; i++)
{
if (min_value > move_value[i])
min_value = move_value[i];
else
continue;
}
set_mat_pix(&dst, x, y, min_value);
}
}
//获取角点坐标
float max_value; int flag; Point max_loc; float value;
for (int y = half_kenal; y < src->rows - half_kenal; )
{
for (int x = half_kenal; x < src->cols - half_kenal; )
{
max_value = 0;
value = 0;
flag = 0;
max_loc.x = -1;
max_loc.y = -1;
//计算点(x,y)位中心的kenal的局部最大值
for (int winy = -half_kenal; winy <= half_kenal; winy++)
{
for (int winx = -half_kenal; winx <= half_kenal; winx++)
{
value = get_pix(&dst, x + winx, y + winy);
if (value > max_value)
{
max_value = value;
max_loc.x = x + winx;
max_loc.y = y + winy;
flag = 1;
}
}
}
//判断是否是角点
if (flag == 1 && (max_value > threshold))
{
cor_point->push_back(max_loc);
}
x += kenal;
}
y += kenal;
}
}
int corner()
{
Mat src, src_gray;
int k = 5;
float threshold = 254;
vector<Point>corner_point; //定义一个Point类型的容器(动态数组)
vector<Point>::iterator itr; //定义迭代器名称
src = imread("..//house.png");
imshow("原图", src);
if (src.empty())
{
cout << "加载图像失败!!!" << endl;
return -1;
}
cvtColor(src, src_gray, COLOR_RGB2GRAY);//将图像转换为灰度图像
Moravec(&src_gray, k, threshold, &corner_point);
for (itr = corner_point.begin(); itr < corner_point.end(); itr++)
circle(src, *itr, 5, Scalar(255,0,0),2);
namedWindow("角点检测结果");
imshow("角点检测结果", src);
waitKey(0);
return 0;
}
实现效果:
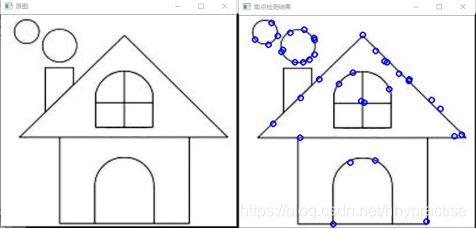
Moravec算子提取角点实验结果如图4所示。
Moravec算子提取角点:
3、掌握图像的纹理分析算法,理解对比度、熵、角二阶矩等纹理测度的几何意义,并能够将纹理特征描述的数学语言转换成程序描述。
本次实验我着重使用的是LBP纹理特征提取法,LBP(Local Binary Pattern,局部二值模式)是一种用来描述图像局部纹理特征的算子;它具有旋转不变性和灰度不变性等显著的优点,提取的特征是图像的局部的纹理特征。对比度指的是一幅图像中明暗区域最亮的白和最暗的黑之间不同亮度层级的测量,差异范围越大代表对比越大,差异范围越小代表对比越小。熵度量影像中纹理特征的复杂程度或非均匀度,若纹理复杂,信息量大,熵值较大。角二阶矩是一种对图像灰度分布均匀性的度量,当图像灰度分布比较均匀时,角二阶矩值较大;反之,角二阶矩的值则较小。LBP的主要实现代码如下所示:
Mat src, gray_src;
int lbp()
{
src = imread("..//xiaozhan.png");
if (!src.data)
{
cout << "图片未找到" << endl;
return -1;
}
namedWindow("原始图像", 1);//创建窗口
imshow("原始图像", src);
cvtColor(src, gray_src, CV_BGR2GRAY);
int width = src.cols - 2;
int hight = src.rows - 2;
Mat lbpImg = Mat::zeros(hight, width, CV_8UC1);
for (int row = 1; row < src.rows - 1; row++)
{
for (int col = 1; col < src.cols - 1; col++)
{
uchar c = gray_src.at<uchar>(row, col);
uchar code = 0;
code |= (gray_src.at<uchar>(row - 1, col - 1) > c) << 7;
code |= (gray_src.at<uchar>(row - 1, col) > c) << 6;
code |= (gray_src.at<uchar>(row - 1, col + 1) > c) << 5;
code |= (gray_src.at<uchar>(row, col + 1) > c) << 4;
code |= (gray_src.at<uchar>(row + 1, col + 1) > c) << 3;
code |= (gray_src.at<uchar>(row + 1, col) > c) << 2;
code |= (gray_src.at<uchar>(row + 1, col - 1) > c) << 1;
code |= (gray_src.at<uchar>(row, col) > c) << 0;
lbpImg.at<uchar>(row - 1, col - 1) = code;}}
namedWindow("LBP纹理特征提取", 1);
imshow("LBP纹理特征提取", lbpImg);
Expand_LBP_demo(0, 0);
waitKey(0);
return 0;}
void Expand_LBP_demo(int, void *)
{
int offset = current_radius * 2;
Mat elbpImg = Mat::zeros(gray_src.rows - offset, gray_src.cols - offset, CV_8UC1);
int numNeighbor = 8;
for (int n = 0; n < numNeighbor; n++)
{
float x = current_radius * cos((2 * CV_PI*n) / numNeighbor);
float y = current_radius * (-sin((2 * CV_PI*n) / numNeighbor));
int fx = static_cast<int>(floor(x)); //向下取整,它返回的是小于或等于函数参数,并且与之最接近的整数
int fy = static_cast<int>(floor(y));
int cx = static_cast<int>(ceil(x)); //向上取整,它返回的是大于或等于函数参数,并且与之最接近的整数
int cy = static_cast<int>(ceil(y));
float ty = y - fy;
float tx = x = fx;
float w1 = (1 - tx)*(1 - ty);
float w2 = (tx)*(1 - ty);
float w3 = (1 - tx)*(ty);
float w4 = (tx)*(ty);
for (int row = current_radius; row < (gray_src.rows - current_radius); row++)
{
for (int col = current_radius; col < (gray_src.cols - current_radius); col++)
{
float t = w1 * gray_src.at<uchar>(row + fy, col + fx) + w2 * gray_src.at<uchar>(row + fy, col + cx) +
w3 * gray_src.at<uchar>(row + cy, col + fx) + w4 * gray_src.at<uchar>(row + cy, col + cx);
elbpImg.at<uchar>(row - current_radius, col - current_radius) +=
((t > gray_src.at<uchar>(row, col)) && (abs(t - gray_src.at<uchar>(row, col)) > std::numeric_limits<float>::epsilon())) << n;}}
namedWindow("扩展的LBP纹理特征提取",1);
imshow("扩展的LBP纹理特征提取", elbpImg);}}
实现效果:
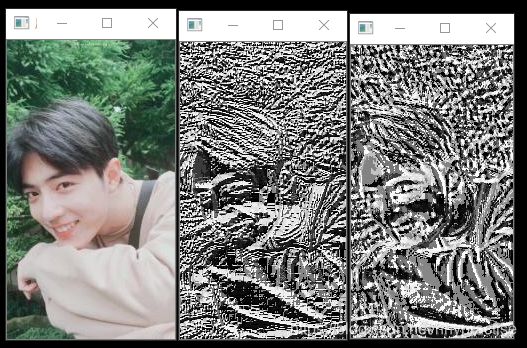
纹理分析LBP算子实验结果如图5所示。
LBP检测结果:
合集入口
测试资源入口