异常检测算法之局部异常因子算法-Local Outlier Factor(LOF)

此文章参考好多篇文章综合整理而成！

0、简介

在数据挖掘方面，经常需要在做特征工程和模型训练之前对数据进行清洗，剔除无效数据和异常数据。异常检测也是数据挖掘的一个方向，用于反作弊、伪基站、金融诈骗等领域。
　　异常检测方法，针对不同的数据形式，有不同的实现方法。常用的有基于分布的方法，在上、下α分位点之外的值认为是异常值（如下图），对于属性值常用此类方法。基于距离的方法，适用于二维或高维坐标体系内异常点的判别，例如二维平面坐标或经纬度空间坐标下异常点识别，可用此类方法。

这次要介绍一下一种基于距离的异常检测算法，局部异常因子LOF算法（Local Outlier Factor），其在中等高维数据集上执行异常值检测的另一种比较有效的算法。

1、算法定义

LOF算法（Local Outlier Factor，局部离群因子检测方法），是一种无监督的离群检测方法，是基于密度的离群点检测方法中一个比较有代表性的算法。该算法会给数据集中的每个点计算一个离群因子LOF，通过判断LOF是否接近于1来判定是否是离群因子。若LOF远大于1，则认为是离群因子，接近于1，则是正常点。
如下图：

2、算法思想

LOF通过计算一个数值score来反映一个样本的异常程度。这个数值的大致意思是：一个样本点周围的样本点所处位置的平均密度比上该样本点所在位置的密度。比值越大于1，则该点所在位置的密度越小于其周围样本所在位置的密度，这个点就越有可能是异常点。关于密度等理论概念，详见下面介绍。
　　用视觉直观的感受一下下图，对于C1集合的点，整体间距，密度，分散情况较为均匀一致，可以认为是同一簇；对于C2集合的点，同样可认为是一簇。o1、o2点相对孤立，可以认为是异常点或离散点。现在的问题是，如何实现算法的通用性，可以满足C1和C2这种密度分散情况迥异的集合的异常点识别。LOF可以实现我们的目标。
　　
下面介绍LOF算法的相关定义：
1)对象p的k距离
对于正整数k，对象p的第k距离可记作k-distance§。在样本空间中，存在对象o，它与对象p之间的距离基座d(p,o)。如果满足以下两个条件，我们则认为k-distance§=d(p,o)：
1)在样本空间中，至少存在k个对象q，使得d(p,q)<=d(d,o)；
2)在样本空间中，至多存在k-1个对象q，使得d(p,q) k−distance§=max|||p−o|||显然易见，如果使用k−distance§来量化对象p的局部空间区域范围，那么对于对象密度较大的区域， k−distance§值较小，而对象密度较小的区域，k−distance§值较大。
p的第k距离，也就是距离p第k远的点的距离，不包括p，如下图
　　　　
2) k-distance neighborhood of p：第k距离邻域
　　已知对象p的第k距离，那么，与对象p之间距离小于等于k−distance§的对象集合称为对象p的第k距离邻域，即点p的第k距离邻域，就是p的第k距离即以内的所有点，包括第k距离。记作：Nk§
该邻域其实是以p为中心，k−distance§为半径的区域内所有对象的集合（不包括p本身）。由于可能同时存在多个第k距离的数据，因此该集合至少包括k个对象即p的第k邻域点的个数 |Nk§|≥k。可以想象，离群度越大的对象的范围往往比较大，而离群度比较小的对象范围小。

3) reach-distance：对象p相对于对象o的可达距离
公式：reachdist(p,o)=max{k−distance(o),||p−o||}
也就是说，如果对象p远离对象o，则两者之间的可达距离就是它们之间的实际距离，但是如果它们足够近，则实际距离用o的k距离代替。
　点o到点p的第k可达距离定义为：
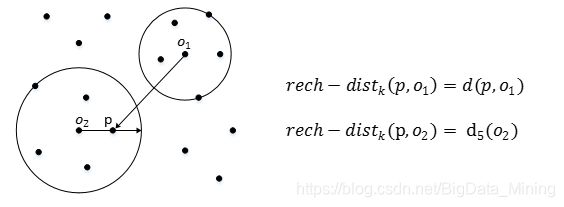
　　　reach−distancek(p,o)=max{k−distance(o),d(p,o)}
　也就是，点o到点p的第k可达距离，至少是o的第k距离，或者为o、p间的真实距离。这也意味着，离点o最近的k个点，o到它们的可达距离被认为相等，且都等于dk(o)。
　　如下图，o1到p的第5可达距离为d(p,o1)，o2到p的第5可达距离为d5(o2)。
　　　　
4) local reachability density：局部可达密度
　　点ｐ的局部可达密度表示为：
　　　　
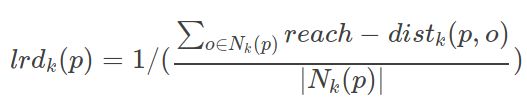
对象p的局部可达密度定义为p的k最近邻点的平均可达密度的倒数，即点p的第k邻域内点到p的平均可达距离的倒数。
　 注意，是p的邻域点Nk§到p的可达距离，不是p到Nk§的可达距离，一定要弄清楚关系。并且，如果有重复点，那么分母的可达距离之和有可能为0，则会导致lrd变为无限大，下面还会继续提到这一点。
　　这个值的含义可以这样理解，首先这代表一个密度，密度越高，我们认为越可能属于同一簇，密度越低，越可能是离群点。如果p和周围邻域点是同一簇，那么可达距离越可能为较小的dk(o)，导致可达距离之和较小，密度值较高；如果p和周围邻居点较远，那么可达距离可能都会取较大值d(p,o)，导致密度较小，越可能是离群点。
　　
5) local outlier factor：局部离群因子
　　点p的局部离群因子表示为：
　　　　
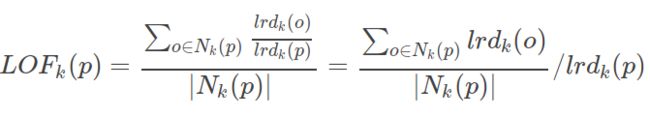
　　表示点p的邻域点Nk§的局部可达密度与点p的局部可达密度之比的平均数，其表示p是离群点的程度。
　　如果这个比值越接近1，说明p的其邻域点密度差不多，p可能和邻域同属一簇；如果这个比值越小于1，说明p的密度高于其邻域点密度，p为密集点；如果这个比值越大于1，说明p的密度小于其邻域点密度，p越可能是异常点。
　　如果对象p不是局部离群点，则LOF§接近于1。即p是局部离群点的程度较小，对象o的局部可达密度和对象p的局部可达密度相似，最后所得的LOF§值应该接近1。相反，p是局部离群点的程度越大，最后所得的LOF§值越高。通过这种方式就能在样本空间数据分布不均匀的情况下也可以准确发现离群点。

现在概念定义已经介绍完了，现在再回过头来看一下lof的思想，主要是通过比较每个点p和其邻域点的密度来判断该点是否为异常点，如果点p的密度越低，越可能被认定是异常点。至于密度，是通过点之间的距离来计算的，点之间距离越远，密度越低，距离越近，密度越高，完全符合我们的理解。而且，因为lof对密度的是通过点的第k邻域来计算，而不是全局计算，因此得名为“局部”异常因子。这样，对于第3张图的两种数据集C1和C2，lof完全可以正确处理，而不会因为数据密度分散情况不同而错误的将正常点判定为异常点。

3、python代码实现

import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import LocalOutlierFactor

np.random.seed(42)
#np.random.seed(0) ; np.random.rand(4) 
#当我们设置相同的seed，每次生成的随机数相同。如果不设置seed，则每次会生成不同的随机数

# Generate train data 生成训练集
X = 0.3 * np.random.randn(100, 2)
# Generate some abnormal novel observations 生成一些异常新颖的观察
X_outliers = np.random.uniform(low=-4, high=4, size=(20, 2)) 
X = np.r_[X + 2, X - 2, X_outliers] #np.r_是将一系列的序列合并到一个数组中
#y = np.r_[[0,2,0], [1,2,3],[4,5,6]]

# fit the model 训练模型
clf = LocalOutlierFactor.LocalOutlierFactor(n_neighbors=20)             #n_neighbors临近距离，默认20
clf.fit(X)

#predict预测
y_pred = clf.fit_predict(X)
y_pred_outliers = y_pred[200:]
#clf.get_params() #得到参数


# plot画图
xx, yy = np.meshgrid(np.linspace(-5, 5, 50), np.linspace(-5, 5, 50))
Z = clf._decision_function(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

plt.title("Local Outlier Factor (LOF)")
plt.contourf(xx, yy, Z, cmap=plt.cm.Blues_r)

a = plt.scatter(X[:200, 0], X[:200, 1], c='white',
            edgecolor='k', s=20)
b = plt.scatter(X[200:, 0], X[200:, 1], c='red',
            edgecolor='k', s=20)
plt.axis('tight')
plt.xlim((-5, 5))
plt.ylim((-5, 5))
plt.legend([a, b],
       ["normal observations",
        "abnormal observations"],
       loc="upper left")
plt.show()

在sklearn包里面有LOF的库，可以直接调用。
核心代码：

clf=LocalOutlierFactor(n_neighbors=20,algorithm='auto',contamination=0.1,n_jobs=-1,p=2)
●n_neighbors=20:即LOF算法中的k的值，检测的邻域点个数超过样本数则使用所有的样本进行检测
●algorithm = 'auto'：使用的求解算法，使用默认值即可
●contamination = 0.1：范围为 (0, 0.5)，表示样本中的异常点比例，默认为 0.1
● n_jobs = -1：并行任务数，设置为-1表示使用所有CPU进行工作
● p = 2：距离度量函数，默认使用欧式距离。（其他距离模型使用较少，这里不作介绍）

clf.fit(data)

无监督学习，只需要传入训练数据data，就可以训练出LOF算法模型，不过输入数据的维度至少是二维

clf.kneighbors(data)
●获取到k距离邻居内的每个点到中心点的距离，并从小到大排列
●返回2nk数组，包含[距离，样本检索]
clf.decision_function(data)
●获取每个样本点的LOF值，不过输出结果是LOF值的相反数，需要取反
●这个函数是在clf.predict(data)的基础上进行改进的，会有更多的功能。
●clf.predict(data)会给出异常点的判断，异常值返回-1，正常值返回1；