采样之蒙特卡罗方法

   随机采样方法

    蒙特卡洛（Monte Carlo）方法是二十世纪四十年代中期由于科学技术的发展和电子计算机的发明，而被提出的一种以概率统计理论为基础的数值计算方法。它的核心思想就是使用随机数（或更常见的伪随机数）来解决一些复杂的计算问题。

   模拟方法:是一种基于“随机数”的计算方法，基于数值采样的近似推断方法,也被称为蒙特卡罗( MonteCarlo )方法、随机模拟方法。

    通常均匀分布    的样本，即我们熟悉的类rand()函数，可以由线性同余发生器生成；而其他的随机分布都可以在均匀分布的基础上，通过某种函数变换得到，比如，正态分布可以通过Box-Muller变换得到。然而，这种变换依赖于计算目标分布的积分的反函数，当目标分布的形式很复杂，或者是高维分布时，很难简单变换得到。

当一个问题无法用分析的方法来求精确解，此时通常只能去推断该问题的近似解，而随机模拟(MCMC)就是求解近似解的一种强有力的方法。

     随机模拟的核心就是对一个分布进行抽样(Sampling)。

   Monte Carlo 方法有这些

    产生独立样本
        基本方法:概率积分变换(第一部分已讲)
        接受—拒绝(舍选)采样
        重要性采样
   产生相关样本:

      Markov Chain Monte Carlo
      Metropolis-Hastings算法
      Gibbs Sampler 

   直接采样

    通过对均匀分布采样，实现对任意分布采样。

    一般而言均匀分布 Uniform(0,1)的样本是相对容易生成的。 通过线性同余发生器可以生成伪随机数，我们用确定性算法生成[0,1]之间的伪随机数序列后，这些序列的各种统计指标和均匀分布 Uniform(0,1) 的理论计算结果非常接近。这样的伪随机序列就有比较好的统计性质，可以被当成真实的随机数使用。

而我们常见的概率分布，无论是连续的还是离散的帆布，都可以基于Uniform(0,1)的样本生成。

    直接采样步骤：

1. 从Uniform(0,1)随机产生一个样本z
2. 另z=h(y)，其中h(y)为y的累积概率分布CDF
3. 计算
4. 结果y为对p(y)的采样

    Note：需要知道累积概率分布的解析表达式，且累积概率分布函数存在反函数。但是如果h(x)不能确定或者没有无法解析求逆则直接抽样不再合适。对于复杂的现实模型其实是不常用的。

   接受-拒绝采样（Acceptance-Rejection Sampling）

    简称拒绝采样，基本思想：假设我们需要对一个分布f(x)进行采样，但是却很难直接进行采样，所以我们想通过另外一个容易采样的分布g(x)的样本，用某种机制去除掉一些样本，从而使得剩下的样本就是来自与所求分布f(x)的样本。

   采样过程

 

   

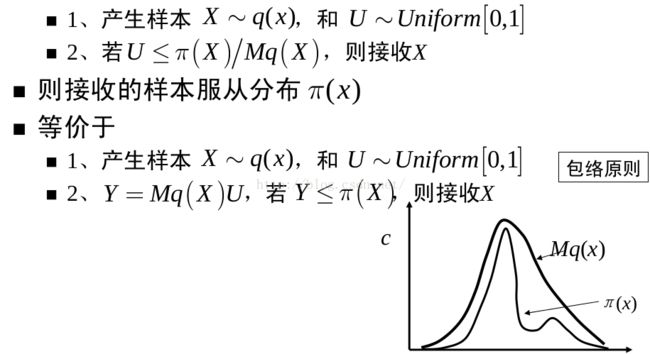
    下面这张图很好地阐释了拒绝采样的基本思想。假设我们想对 PDF 为 p(x)p(x) 的函数进行采样，但是由于种种原因（例如这个函数很复杂），对其进行采样是相对困难的。但是另外一个 PDF 为 q(x)q(x) 的函数则相对容易采样，例如采用 Inverse CDF 方法可以很容易对对它进行采样，甚至 q(x)q(x) 就是一个均匀分布（别忘了计算机可以直接进行采样的分布就只有均匀分布）。那么，当我们将 q(x)q(x) 与一个常数 MM 相乘之后，可以实现下图所示之关系，即 M⋅q(x)M⋅q(x) 将 p(x)p(x) 完全“罩住”。

    然后重复如下步骤，直到获得 mm 个被接受的采样点：

• 从 q(x) 中获得一个随机采样点 x(i)
  
• 对于 xi 计算接受概率（acceptance probability）
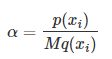
• 从 Uniform(0,1) 中随机生成一个值，用 u表示
• 如果 α≥u，则接受 xi 作为一个来自 p(x)的采样值，否则就拒绝 xi 并回到第一步

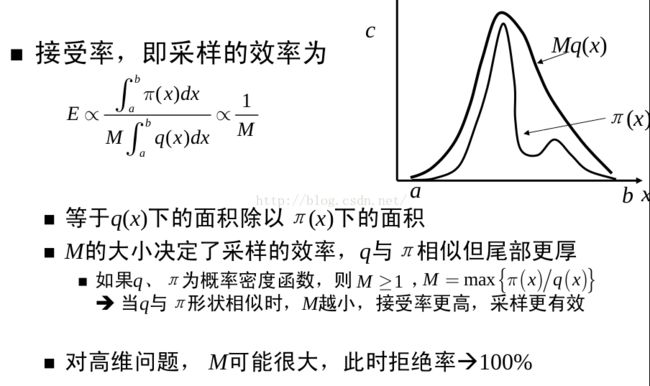
    接受率问题

    现在有一个问题，m怎么求？

    其实也很简单，看图有 mq(x) >= p(x)，那么m>= p(x) / q(x)，我们求p(x) / q(x)的最大值，即为m。

   随机采样算法的实现

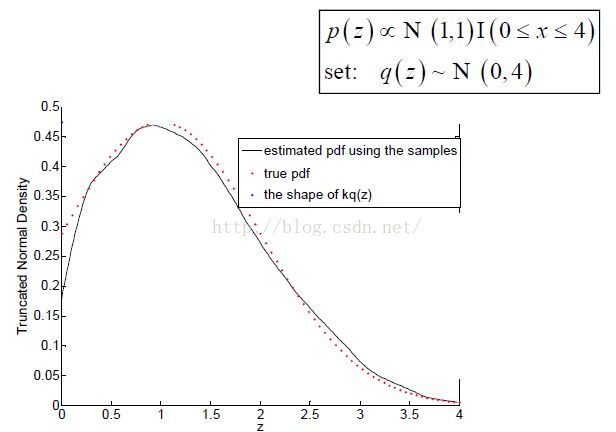
    对截断正态分布[Truncated normal distribution]采样

    

# -*- coding: utf-8 -*-
from scipy import optimize
from scipy.stats import norm, uniform
import numpy as np
import matplotlib.pyplot as plt

trunc = [0, 4]  # 实际分布截断坐标点
p = [1, 1]  # 实际分布参数（均值，标准差）
q = [0, 2]  # 建议分布参数（均值，标准差）

def k(p, q, trunc):
    '''
    求k = max_x{p(x)/q(x)}
    '''
    #  loc代表了均值, scale代表标准差
    #  cdf(x, loc=0, scale=1)；输入x，返回概率，既密度函数的面积
    #  pdf(x, loc=0, scale=1)；输入x，返回概率密度函数

    trunc_factor = (norm.cdf(trunc[1], p[0], p[1]) - norm.cdf(trunc[0], p[0], p[1])) / p[1]
    print(trunc_factor)
    exp_k = lambda x: norm.pdf(x, p[0], p[1]) / norm.pdf(x, q[0], q[1]) / trunc_factor
    # exp_k = lambda x: norm.pdf(x, p[0], p[1]) / norm.pdf(x, q[0], q[1])#未截断的
    max_x = optimize.minimize_scalar(lambda x: -norm.pdf(x, p[0], p[1]) / norm.pdf(x, q[0], q[1]), bounds=trunc)['x']
    k = exp_k(max_x)
    print("max_x = {}\nk = {}\n".format(max_x, k))
    return k, max_x

def show_k(k, max_x, p, q, trunc):
    '''
    求出k后绘制建议分布概率密度和实际分布概率密度图，看p(x)和k*q(x)是否相切
    '''
    # x = np.linspace(norm.ppf(0.01, loc=p[0], scale=p[1]), norm.ppf(0.99, loc=p[0], scale=p[1]), N)
    x = np.linspace(trunc[0], trunc[1], 100)
    q = k * norm.pdf(x, loc=q[0], scale=q[1])  # 建议分布概率密度
    p = norm.pdf(x, loc=p[0], scale=p[1]) / (
        norm.cdf(trunc[1], p[0], p[1]) - norm.cdf(trunc[0], p[0], p[1]))  # 实际分布概率密度
    plt.plot(x, q, 'r')
    plt.plot(x, p, 'g')
    plt.axvline(max_x, color='b', label=max_x)  # 相切点
    plt.text(max_x, 0, str(round(max_x, 2)))
    plt.show()
def acc_rej_sample(k, p, q, trunc, N):
    '''
    接受拒绝采样
    :param N: 采样数
    '''
    # rvs(loc=0, scale=1, size=1, random_state=None)：产生随机数
    z = norm.rvs(loc=q[0], scale=q[1], size=N)  # 从建议分布采样
    mu = uniform.rvs(size=N)  # 从均匀分布采样
    z = z[(mu <= norm.pdf(z, p[0], p[1]) / (k * norm.pdf(z, q[0], q[1])))]  # 接受-拒绝采样
    z = z[z >= trunc[0]]
    z = z[z <= trunc[1]]
    # print("sampled z = \n{}\n".format(z))
    return z


def show_z(z, p, trunc):
    '''
    采样得到采样样本z后看是否采样得到实际正态分布的近似
    '''
    # 采样分布概率密度图
    cnts, bins = np.histogram(z, bins=500, normed=True)
    bins = (bins[:-1] + bins[1:]) / 2
    plt.plot(bins, cnts, label='sampling dist')
    # plt.hist(z, bins=500, normed=True)

    # 实际分布概率密度图（截断后的）
    x = np.linspace(trunc[0], trunc[1], 100)
    trunc_factor = (norm.cdf(trunc[1], p[0], p[1]) - norm.cdf(trunc[0], p[0], p[1])) / p[1]
    plt.plot(x, norm.pdf(x, loc=p[0], scale=p[1]) / trunc_factor, 'r', label='real dist')
    plt.legend()
    plt.show()


if __name__ == '__main__':
    k, max_x = k(p, q, trunc)
    # show_k(k, max_x, p, q, trunc)
    z = acc_rej_sample(k, p, q, trunc, N=10000000)
    show_z(z, p, trunc)

    

截断面积trunc_factor：0.839994848037

k最大时的x点max_x = 1.333333333395553

求解出的k值：k = 2.812780139369929

 

采样结果同真实结果的比较：

 

   参考文献：

           https://blog.csdn.net/u010159842/article/details/78959177

           https://www.jianshu.com/p/3d30070932a8

           https://blog.csdn.net/baimafujinji/article/details/51407703

 

   

 

 

转载于:https://www.cnblogs.com/171207xiaohutu/p/9480119.html