心跳信号分类预测（天池数据集）

        前些时间，做了个阿里天池的练习赛，心跳预测。说是练习赛，实际也没赛，因为最后的结果也没拿去提交、上传之类的，最后做了个小展示，权当做练手，在这里和大家分享一下整体的思路，希望可以给后来者一些启发。期待可以和大家一起沟通交流，指出不足之处，相互学习，共同进步。

        先回顾一下先前的题目：

        数据集见下面链接，也不用大家花C币了，直接在下面链接就能下载。

        零基础入门数据挖掘-心跳信号分类预测赛题与数据-天池大赛-阿里云天池

一、赛题数据

赛题以预测心电图心跳信号类别为任务，数据集报名后可见并可下载，该数据来自某平台心电图数据记录，总数据量超过20万，主要为1列心跳信号序列数据，其中每个样本的信号序列采样频次一致，长度相等。为了保证比赛的公平性，将会从中抽取10万条作为训练集，2万条作为测试集A，2万条作为测试集B，同时会对心跳信号类别（label）信息进行脱敏。

字段表

Field	Description
id	为心跳信号分配的唯一标识
heartbeat_signals	心跳信号序列
label	心跳信号类别（0、1、2、3）

二、评测标准

选手需提交4种不同心跳信号预测的概率，选手提交结果与实际心跳类型结果进行对比，求预测的概率与真实值差值的绝对值（越小越好）。

具体计算公式如下：

针对某一个信号，若真实值为[y_1,y_2,y_3,y_4][y1​,y2​,y3​,y4​],模型预测概率值为[a_1,a_2,a_3,a_4][a1​,a2​,a3​,a4​],那么该模型的平均指标abs-sumabs−sum为
{abs-sum={\mathop{ \sum }\limits_{{j=1}}^{{n}}{{\mathop{ \sum }\limits_{{i=1}}^{{4}}{{ \left| {y\mathop{{}}\nolimits_{{i}}-a\mathop{{}}\nolimits_{{i}}} \right| }}}}}}abs−sum=j=1∑n​i=1∑4​∣yi​−ai​∣
例如，心跳信号为1，会通过编码转成[0,1,0,0][0,1,0,0]，预测不同心跳信号概率为[0.1,0.7,0.1,0.1][0.1,0.7,0.1,0.1]，那么这个预测结果的abs-sumabs−sum为
{abs-sum={ \left| {0.1-0} \right| }+{ \left| {0.7-1} \right| }+{ \left| {0.1-0} \right| }+{ \left| {0.1-0} \right| }=0.6}abs−sum=∣0.1−0∣+∣0.7−1∣+∣0.1−0∣+∣0.1−0∣=0.6     

  

三、结果提交

提交前请确保预测结果的格式与sample_submit.csv中的格式一致，以及提交文件后缀名为csv。

形式如下：

id,label_0,label_1,label_2,label_3
100000,0,0,0,0
100001,0,0,0,0
100002,0,0,0,0
100003,0,0,0,0

        原本题目中还有提交结果，我在这里只做了前两部分。

        接下来具体将从处理分析数据、构建模型、结果分析以及对模型的改进与优化四个方面阐述。

---

  一、数据处理    

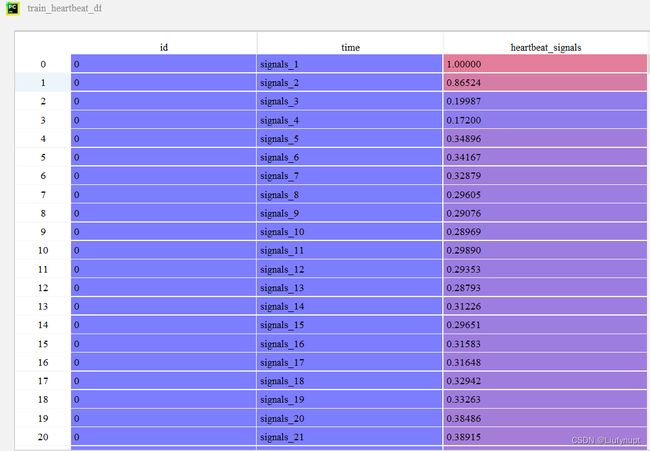
        首先，拿到原始数的后，先查看了数据的大致情况，查看数据的形式、数量，以便确定后续的处理方法。

        100000条数据，每条数据内是由","划分的205个数据，要想对其进行处理，首先要对数据进行分列重组，以便进行后续处理。（个人习惯将标签放到前面）

data=pd.read_csv('C:\\Users\\LFY\\Desktop\\\\train0.csv')

data.head()

data1 = data['heartbeat_signals'].str.split(',', expand=True)   # 将数据按‘,’拆分
new_names = ['signals_' + str(x + 1) for x in range(205)]   # 为新生成的列取名
data1.columns = new_names  # 重命名新生成的列名
data1["label"] = data["label"]  #加入标签列
data1 = pd.DataFrame(data1,dtype=np.float64)    # 转化为数组形式

#把label移到最前面

col=list(data1)
col.index('label')
col.insert(0,col.pop(col.index('label')))
data2=data1.loc[:,col]

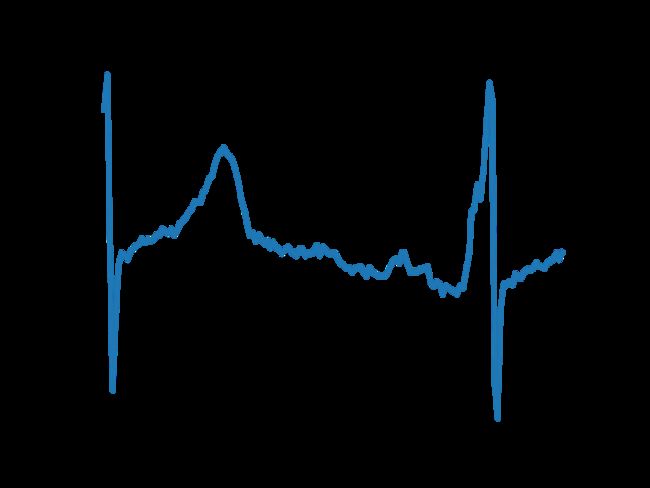
        将数据拆分后，更容易观察数据的特征。用data.head（）查看数据，进而对数据进行探索性分析（对数据不明所以，所以先做个图看看）

        观察数据可知，这个波形类似于心电图，结合题目背景，猜想每条数据可能都是取自某导联的一段心电图。无独有偶，心电监测的采样频率正是12000Hz，折合到每秒采样200次，与每条数据的205个值非常接近。由此，我们有理由猜测，该数据主要是一个心电检测12000Hz，每秒200个采样点，数据规模为100000条*205个维度的心跳数据。该数据集很可能是一个十万段长度为一秒左右的心跳数据。

        对数据集中的训练集进行简单的处理后发现不存在缺失值与异常值，对各个类别样本进行统计。发现样本存在两个较为明显的问题。

1.样本不平衡

        对于分类模型而言，样本不均衡的问题很重要。标签为0类、1类、2类、3类的样本分别有64327、3562、14199、17912条。第0类的占比64.327%，但第1类的仅占总样本数的3.562%，样本数最多的第0类是样本数最少的第1类的将近20倍，这就导致了模型会学习到训练集中这种不均衡样本比例的先验信息，以至于在实际预测时就会对多数类别有侧重。故需要对样本不平衡问题先进行处理。

        在数据处理时需要对训练集进行数据增强和扩增，将样本数量较少的那些类中加工出更多数据的表示，提高原数据集的数量及质量，从而提高模型的学习效果。因此需要将第1类、第2类、第3类的样本进行扩增，使各类样本数达到均衡。

        由于原始数据是心电数据，因此采用Scale（缩放）处理的方法。该方法的本质是根据某一类随时间变化的心跳的波形，对其进行一个缩放作用，从而生成一个新的数据但不改变其波峰波谷的这些特征本质。最终进行样本扩增后，四个类别的样本数基本一致。

scale的实现也很简单，代码如下：

def DA_Scaling(X, sigma=0.1):
    scalingFactor = np.random.normal(loc=1.0, scale=sigma, size=(1,X.shape[1])) 
    myNoise = np.matmul(np.ones((X.shape[0],1)), scalingFactor)
    return X*myNoise

具体过程如下，以一类样本扩充为例：一类样本做数据增强后，样本量扩增了16倍，数量基本与0类样本大致接近

​
#对标签为1的样本进行数据增强
idxs = data3.query('label==1').index
datmp = data3.iloc[idxs,:].reset_index(drop=True)
datmp['label'] = 1
data11=DA_Scaling(datmp, sigma=0.1)
for ii in np.arange(16):
    data11 = pd.concat((data11, datmp), axis=0).reset_index(drop=True)
data11['label']=1

​#打乱数据，使得不同标签样本均匀混合
data_train = data_train.sample(frac=1, random_state=2022).reset_index(drop=True)

二、三类样本扩充同理，扩增至与0类样本数量相近

扩增之后的各类样本数量如下：

数据增强后的均衡数据集

类别	样本数
0类	22404
1类	22164
2类	24584
3类	30850

2.数据末尾持续0

        部分数据中的末尾部分持续为0，对此异常情况推测是进行心跳采样时还没有到1秒钟的情况下，就摘下电极片，摘下后数据都为0，而这部分持续为0的维度本不是心跳的特征，因此在数据处理时将其剔除。具体处理方式为：先将末尾的0转化为NaN，再将原本行数据转化为列，每个时间

#数据处理：删去样本末尾的0，转为NaN
def assign_nan(data):
    nptmp = data.to_numpy()
    #    print(nptmp.shape)

    left_idxs = np.arange(nptmp.shape[0])
    for ii in np.arange(nptmp.shape[1])[::-1]:
        idxs = np.where(nptmp[left_idxs, ii] <= 1.e-5)[0]
        if idxs.size > 0:
            nptmp[left_idxs[idxs], ii] = np.nan
            left_idxs = left_idxs[idxs]
        #            print(f'{ii}: {left_idxs.size}, |, {left_idxs}')
        else:
            #            print(f'Finished at {ii}')
            break

    # nptmp[:, :2] = np.nan
    return pd.DataFrame(nptmp[:,:], index=data.index, columns=data.columns[:])

data3=assign_nan(data2)

# 对心电特征进行行转列处理，同时为每个心电信号加入时间步特征time
train_heartbeat_df = data_train.iloc[:,1:].stack()
train_heartbeat_df = train_heartbeat_df.reset_index()
train_heartbeat_df.rename(columns={"level_0":"id","level_1":"time", 0:"heartbeat_signals"}, inplace=True)

train_heartbeat_df["heartbeat_signals"] = train_heartbeat_df["heartbeat_signals"].astype(float)

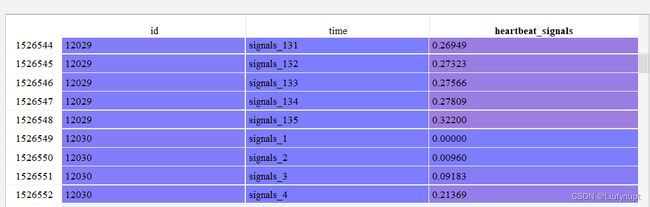
        得到的数据如下图所示，第一列为代表样本编号的id，第二列为对应的时间 ，从signals_1到signals_205分别对应205个时间节点。heartbeat_signals为对应时间的心电信号

而此时的心电信号为0的行已在之前就被转化为NaN，在转化为列数据的时候，被删除掉了，如下图所示，id为12029的心电信号在135之后的信号值都为0，故被剪去。

 处理完数据的不平衡问题和末尾为0的问题后，数据的基本预处理已经完成，进入到下一部分——特征提取

3.特征提取 

        因为数据本身的特点——时间序列数据，故考虑使用时间序列特征提取包：tsfresh进行特征提取

        在tsfresh中，内置了三种特征提取方案，我们可以根据实际情况，去选择不同的特征组合进行提取。除了已经预设的特征组合外，还可以自定义特征组合方式，提取指定的特征。

在这里我使用的是 ComprehensiveFCParameters这一组合，具体其他组合也在这里提供给大家，任选其一即可，我在这里都放出来，以供大家选取使用。

        tips：建议大家在提取特征后，直接就把提取到的特征存下来，因为提取的过程真的蛮久，提取之后，可以直接用存下来的特征去进行之后的步骤，而不用每次都重复这个提取过程

#不同特征提取组合
settings = ComprehensiveFCParameters()

settings  =  MinimalFCParameters ()

settings  =  EfficientFCParameters()


#设置所提取的特征
fc_parameters={
    "length":None,
    "large_standard_deviation":[{"r": 0.05}, {"r": 0.1}],
    "abs_energy":None,
    "absolute_sum_of_changes":None,
    "agg_linear_trend":[{"f_agg":'mean','attr': 'pvalue', 'chunk_len': 2}]
}

#对应的label
data_label=data_train1.iloc[:,0]
#提取默认特征
train_features=extract_relevant_features ( train_heartbeat_df ,data_label,column_id='id', column_sort='time',  default_fc_parameters = settings )
#提取指定特征
# train_features=extract_features ( train_heartbeat_df ,column_id='id', column_sort='time',  default_fc_parameters=fc_parameters )
#所提取出的特征
train_features
#保存特征
train_features.to_csv("100000_statistics_feature.csv")

提取保存完特征之后，就可以用所提取的特征进行建模了

二、模型构建

        具体模型选择随机森林。期中最大的决策树个数为500棵，损失函数选择信息增益，最大特征数为划分时最多考虑n个特征，决策树的最大深度为20，最小叶子节点为1。其他参数均设置为默认数值。

         由于提取到的特征维度较高，直接输入模型会导致模型运行时间过长。故先对提取得到的特征维度进行降维，再输入模型中。具体使用PCA来进行降维

features=pd.read_excel(r'C:\Users\LFY\Desktop\fea.xlsx')
pca=PCA(n_components=39) # 取前39个主成分
features=features.iloc[:,-39:]
min_max_normalizer=preprocessing.MinMaxScaler(feature_range=(0,1))
features=min_max_normalizer.fit_transform(features)
a=pca.fit(features)
results=pca.transform(features)
print(pca.explained_variance_ratio_) # 方差贡献率
#print(results) # 降维后的数据
data=pd.DataFrame(results)

将降维后的数据输入到随机森林模型中，进行分类

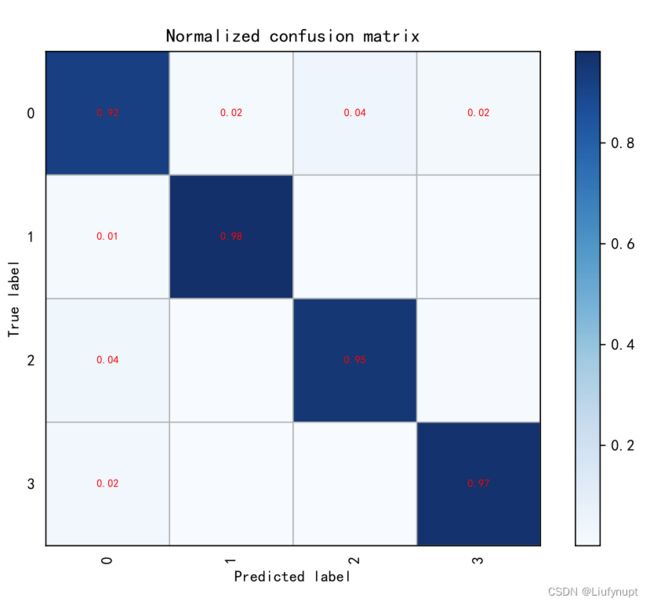
利用准确率、召回率、精确度、F1分数、混淆矩阵、ROC曲线来评价该预测模型的性能。最终结果为：准确率为0.956、召回率为0.955、精确度为0.955、F1分数为0.932。（重复运行5次的平均值）。混淆矩阵如下图所示。不调参时由于没有设置随机森林的深度，导致模型过拟合，在经过调整参数后选择模型的深度为20取得不错的效果。通过结果可以看出模型总的准确率为0.956

 三、结果分析

        模型最后的分类准确率为95.6%（重复运行5次的平均值），平均运行时间时长为561秒。对于疾病类判别的问题，相较于分类正确的样本，我们往往更关注于被错判的样本。

        分析错误的样本能帮住我们找到先前工作中被忽略的部分。分析每一类的特点，首先了解心电图的组成部分，它包括有P波、QRS波、T波、PR段、ST段等。P波是每一组中的第一波，它是由心房除极所产生。QRS波代表两心室除极和最早期复位过程的电位和时间变化。在标准情况下，ST段水平线是以PR段为基线的延长线。正常人的ST段应在等电位线上，有时存在一些轻微的偏移。一次正常的心跳是从P波开始，之后是QRS波，最后是T波。

 第1类心跳信号示例图

        观察第1类如图6所示，该图在TP段间有异常抖动现象，甚至看不清P波的基线，这种情况可能为心房纤颤。

 第2类心跳信号示例图

       观察第2类，如上图所示，QRS波振幅较小而频率高，波形较为抖动，可能为室性心动过速。

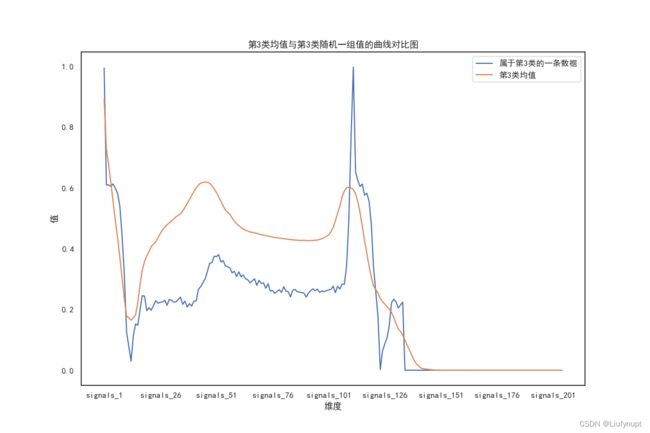
第3类心跳信号示例图

        第3类如上图所示，P波段在图8中几乎观察不到，缺少P波，可能为房室结性早搏。

        下面对错判成的三个类别分别进行分析。首先是被错判为第1类的样本均值，如下图所示。

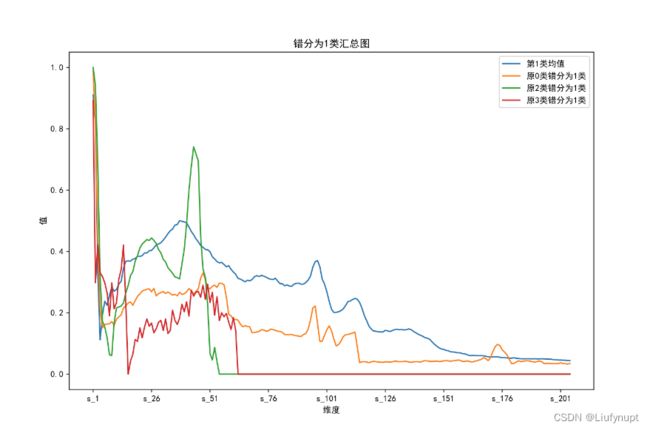
 错判为1类的样本分布图

        上图是当真实标签并不是1类时被模型错判为1类的心电图每个维度的平均值的图。观察正常第1类可以发现基本上看不到P波的基线，一直处于一个向上波动的姿态，且在第76到第126维度上即对应的TP段出现了异常抖动的现象。这些都是典型的第1类即心房纤颤的特征。第0类被错判为第1类的心电图中可以明显看到同样是在第76到126维心跳出现剧烈的波动，且P波同样不明显，因此可以推测模型学到的第1类的特征主要就是在第1维到第50维的P波不明显以及第76到126维上的剧烈波动。观察第2类和第3类被错判为第1类的图可以获得在对这些样本分类时，模型主要是因为P波找不到基线而将其错判为1类。总结可获得模型对第1类所学到的特征着重关注于P波的基线是否可观察。

        其次是被错判为第2类的样本均值，如下图所示。

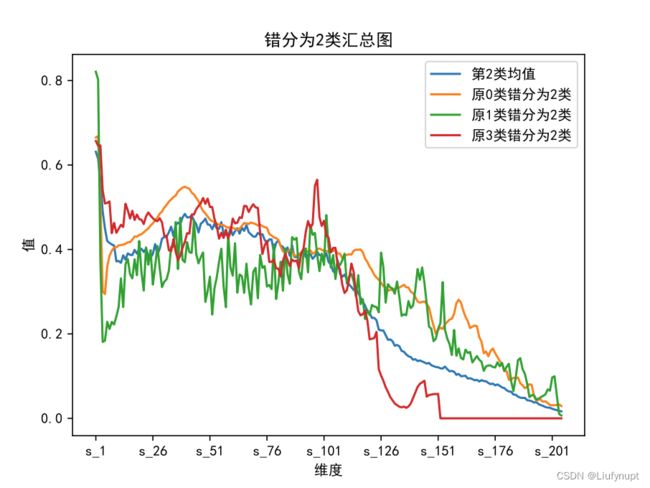
 错判为2类的样本分布图

        被错判为第2类的样本的心电图每个维度的平均值如上图所示，正常情况下第2类所表现出的特征可以看出是从第3到第101维心电数据的QRS波较为抖动，且在这一秒的波形中基本都有抖动情况，被诊断为室性心动过速。观察原始第0类、原始第1类、原始第2类都可以看出他们被错判的主要原因也是由于出现了这一特征，它们的波形都存在着QRS波较小但频率较高的情况，可以推测模型对于第2类心电图所学到的特征主要就是在中间部分QRS波的抖动。

        最后是被错判为第3类的样本均值，如下图所示。

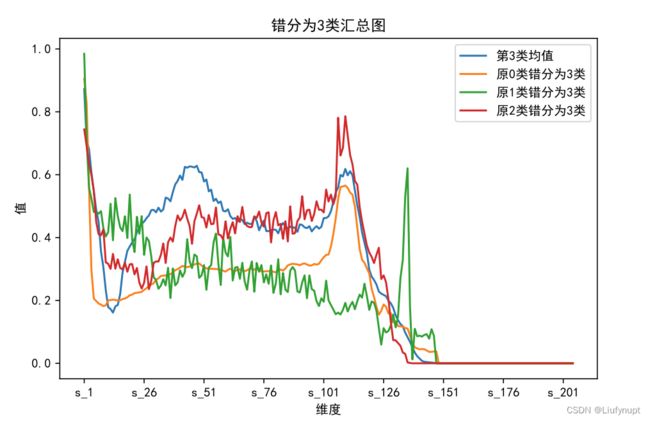
错判为3类的样本分布图

        被错判为第3类的样本的心电图每个维度的平均值如图11所示，正常情况下第3类表现出来的特征为缺少P波即在51维前看不到一个较缓的波谷，观察被错判的另外几个类别都出现了这种情况，即模型对第三类所学习到的特征推测是前51维没有明显的P波存在。

        综上，对于被错判的样本我们可以做出推测是因为它们表现出了其他类型所具有的特征，而这个特征又恰巧是模型较为关注的特征，因此出现样本病例被错判的情况。

四、改进与优化

角度1. 本模型基础上进行优化，增加医学方面的先验知识

        由于模型会出现过分的关注数据中的某些重点特征或由于数据处理不是很充分也可能会学习到一些不好的特征，从而导致将类别错判，为解决这个问题，可以在建立模型时给模型添加一个先验知识，让模型学习到一些关键的特征，例如在本文中可以加入一些心电数据更加关注的特征。另外还可以在构建模型是运用多模态的方法，即可以再加入一个视觉模态之类的，通过多方面的信息来判断病人到底是什么病症，这也是提高模型预测准确度的一个方法。

角度2. 尝试使用更多的模型

        目前，只使用了PCA进行降维，还可以考虑其他一些实用的降维方法，譬如GA遗传算法等方法；建模方面除了随机森林外，还有很多经典的分类模型也可以使用。

角度3. 在可视化方面，增加热力图等图形

五、总结与致谢

在此感谢我的导师和我的舍友们，没有你们的帮助，这个作品绝不会是现在的样子（虽然现在也很稚拙）但我们一起努力的时候，真的很快乐呀，跟着大佬们每天都学到非常多，幸甚至哉！