原生javascript实现树布局算法
其他资源:
1.完整的树状图布局代码
本文目录
-
- 效果展示
- 绘制原则
- 主要难点
- 算法流程1——FirstWalk
- 算法流程2——SecondWalk
- apportion函数
- 通过canvas绘制节点和线
效果展示
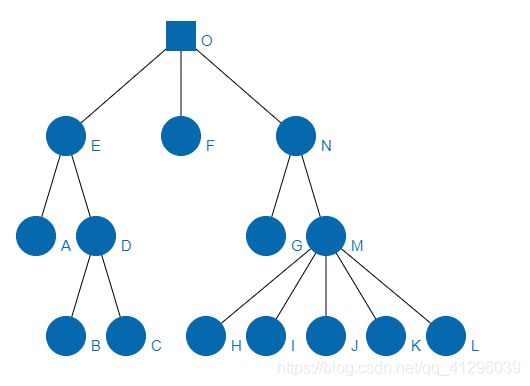
目标:将树结构数据绘制成一个树的图,树结构数据大概是这个样子:
实现:传统javascript语言+html的canvas实现
说明一下,其实网络上的关于树结构的数据有很多种类,这里我只选取了一种类型的数据,如果想要直接使用我这里的算法,可以自己尝试调整数据类型或者调整对应的算法。后面我还针对另一种数据类型做了相应的调整,也就是说完整的代码可以应对两种格式的树结构数据。
let data = [
{
"id": "0",
"name": "O",
"fatherId": "-1",
},
{
"id": "1",
"name": "E",
"fatherId": "0",
},
{
"id": "2",
"name": "F",
"fatherId": "0",
},
{
"id": "3",
"name": "N",
"fatherId": "0",
},
{
"id": "4",
"name": "A",
"fatherId": "1",
},
{
"id": "5",
"name": "D",
"fatherId": "1",
}
];
data.push({
"id":String(data.length),
"name":"G",
"fatherId":"3",
})
data.push({
"id":String(data.length),
"name":"M",
"fatherId":"3",
})
data.push({
"id":String(data.length),
"name":"B",
"fatherId":"5",
})
data.push({
"id":String(data.length),
"name":"C",
"fatherId":"5",
})
data.push({
"id":String(data.length),
"name":"H",
"fatherId":"7",
})
data.push({
"id":String(data.length),
"name":"I",
"fatherId":"7",
})
data.push({
"id":String(data.length),
"name":"J",
"fatherId":"7",
})
data.push({
"id":String(data.length),
"name":"K",
"fatherId":"7",
})
data.push({
"id":String(data.length),
"name":"L",
"fatherId":"7",
})
绘制原则
根据Donald Knuth在论文中的叙述,我们可明白树状图的绘制基本要满足两个原则:
原则1:树的边不应该相互交叉。
原则2:相同深度的所有节点应绘制在同一水平线上。这有助于明确树的结构。
主要难点
在计算规模上,对于一个树的操作肯定是要面对迭代和回溯的,而像这样的对树进行布局的算法,可以说的上是一个NPC问题。
同事我们也注意到,通过所谓“完美”的算法绘制出来的树也是有缺陷的,例如:在面对大规模的数据时,会面临屏幕无法全部显示的现象,同时如果树的高度太高,也会发现容易出现你看了下面忘记上面的现象。这里只是提一下,对于这些问题的解决有兴趣可以自己探索。
算法流程1——FirstWalk
本算法主要依靠了《A Node-Positioning Algorithm for General Trees》这篇文献上的算法。
文献变量说明:
在文献或者代码上可能遇到的变量我尽量会在这个地方说明:
//节点标识
id // 节点的序号,在数组中的位置
name // 节点名称
fatherId // 父节点id
x、y // 该节点位置
child // 孩子的集合
level // 节点的层级
prelim //
modifier //prelim与modifier主要对应于文献的两个变量,用于节点的偏移与修改
rightSiblingId // 右兄弟节点的Id
leftsiblingId // 左兄弟节点的Id
leftNeighbor // 左邻居
论文中主要完成了两个递归,即FIRSTWALK和SECONDWALK。
firstwalk主要是完成树中节点的prelim,我们可以基本认为最后的坐标是prelim加上一些modify的偏移:
firstwalk中的计算逻辑为
1.当前节点是叶节点无左兄弟,prelim记0
2.当前节点是叶节点有左兄弟,prelim是左兄弟prelim加上宽度,即根据左兄弟定位;
3.当前节点非叶节点无左兄弟,prelim是第一个子节点prelim加上最后一个子节点除以二,即根据子节点定位
4.当前节点非叶节点有左兄弟,prelim记左兄弟相对位置,modifier记prelim相对子节点定位修正值,使用apportion修正子孙节点定位
代码部分如下:
function firstWalk(node){
// var space = 65;
// var nodeSize = 30;
var space = 40;
var nodeSize = 20;
if(node.children == null)
{ // 判断该节点是否有子节点
// 如果当前节点为叶子节点
if(node.leftsiblingId!=null)
{
// 该节点有左兄弟,计算相对位置
node.prelim = data[node.leftsiblingId].prelim + space + nodeSize;
}
else //如果该节点没有左兄弟prelim记为0
{
node.prelim = 0 ;
}
}
else // 计算非叶子节点
{
// 先计算所有子节点的位置
var leftPrelim = 0;
var rightPrelim =0;
var nodeChild = null
nodeChild = node.children[0]; // 一个节点的最左孩子
firstWalk(nodeChild);
leftPrelim = node.children[0].prelim;
while(nodeChild.rightSiblingId!=null&&nodeChild.rightSiblingId!=undefined)
{
nodeChild = data[nodeChild.rightSiblingId]
firstWalk(nodeChild);
}
rightPrelim = nodeChild.prelim;
var midPoint = (leftPrelim + rightPrelim)/2 // 定位到子节点集合的中心位置
// 如果当前节点有左兄弟,prelim计算相对位置,计算modifier
if(node.leftsiblingId!=null)
{
node.prelim = data[node.leftsiblingId].prelim +space +nodeSize;
node.modifier = node.prelim - midPoint;
// 计算子树移动距离,当前深度节点分摊偏移
apportion(node);
}
else // 没有左兄弟,prelim记子节点集合的中心位置
{
node.prelim = midPoint;
}
}
}
算法流程2——SecondWalk
secondwalk只是对初始x值加上所有父亲节点的modifier修正值,算得最终x坐标,y坐标可以根据深度直接算出。具体代码如下:
function secondWalk(modSom,node){
if(node!=null)
{
console.log(node.modifier)
// 根据prelim和偏移值计算x,根据深度计算y
node.x = node.prelim + modSom;
node.y = node.level *100+40;
// 遍历子节点,子节点的偏移累加父节点prelim
if(node.children!=null)
{//子节点不等于空
for(var j=0;j<node.children.length;j++)
{
var modifier = 0
if(node.modifier!=null&&node.modifier!=undefined)
modifier =node.modifier
secondWalk(modSom+modifier,node.children[j])
}
}
}
}
apportion函数
而算法中最麻烦的地方在于apportion函数。
apportion函数在firstwalk中,当前节点既有左兄弟又有子节点时发生的一次位置调整,具体逻辑是当子节点定位x坐标大于左兄弟定位x坐标时,当前节点prelim和modifier均累加偏移量。
如果想要具体了解:大家可以看一下这篇博文,作者将apportion阐述的比较清楚
https://blog.csdn.net/zfy920323/article/details/82779764?spm=1001.2014.3001.5501
apportion函数代码为
function apportion(node){
var leftMost = null;
var neighbor = null;
leftMost = node.children[0]; // 当前节点下移一行,取最左孩子
neighbor = data[leftMost.leftNeighbor]; //下移后左节点的左邻居,进行比较
var CompareDepth = 1;
var leftModSum,rightModSum;
while (leftMost!=null&&neighbor!=null)
{
// 左孩子和左孩子节点的邻居节点都存在
// 这两个节点都在,可以进行比较,累加其父节点的modifier(即理想位置)
leftModSum = 0.0;
rightModSum = 0.0;
var ancestorLeftmost = null;
var ancestorNeighbor = null;
ancestorLeftmost = leftMost;
ancestorNeighbor = neighbor;
// 从子节点往上遍历到当前深度
for (var i=0;i<CompareDepth;i++)
{
// 下移一个深度
ancestorLeftmost = data[ancestorLeftmost.fatherId];
ancestorNeighbor = data[ancestorNeighbor.fatherId];
// console.log(i+node.name+"他的ancestorLeftmost节点为"+ancestorLeftmost.name+"、他的ancestorNeighbor节点为"+ancestorNeighbor.name)
if(ancestorLeftmost==null||ancestorNeighbor==null)
continue;
rightModSum += ancestorLeftmost.modifier;
leftModSum += ancestorNeighbor.modifier;
}
var moveDistance = (neighbor.prelim + leftModSum + 80) - (leftMost.prelim + rightModSum);
// 计算后应向右偏移,当前列的所以节点分摊右移
if(moveDistance > 0.0)
{
var tempPtr = null;
tempPtr = node;
var leftsibling = 0;
//往左数到子节点邻居的父节点
while(tempPtr!=null &&ancestorNeighbor!=null&& tempPtr.id!=ancestorNeighbor.id)
{
// 主要用于检测有几个兄弟(用于计算分摊的偏移量)
leftsibling = leftsibling + 1;
tempPtr = data[tempPtr.leftsiblingId];
}
// leftsibling = data[tempPtr.fatherId].children.length
//从当前节点到邻居父节点,对所有节点进行移位
if(tempPtr!=null)
{
var portion = moveDistance/leftsibling;
tempPtr = node;
while(tempPtr!=null &&ancestorNeighbor!=null&&tempPtr!=ancestorNeighbor)
{
tempPtr.prelim = tempPtr.prelim + moveDistance;
tempPtr.modifier = tempPtr.modifier + moveDistance;
moveDistance = moveDistance - portion;
tempPtr = data[tempPtr.leftsiblingId];
}
}
else
{
// return;
}
}
CompareDepth += 1;
if(leftMost.children==null) //leftMost.children[0]==null||leftMost.children[0]==undefined||
{ //当前深度,查找第一个有子节点的,取最左子节点
// console.log(111)
// console.log(leftMost);
leftMost = getLeftMost(node,0,CompareDepth)
// console.log(leftMost)
}
else
leftMost = leftMost.children[0];
if (leftMost!=null&&leftMost.leftNeighbor!=null)
neighbor = data[leftMost.leftNeighbor]
}
}
通过canvas绘制节点和线
这里主要是通过canvas绘图,如果想用svg绘制也是可以,直接对js中的canvas中响应位置做出调整即可,这里也是直接给出代码
function NodeInit(x,y,size,nodeText,nodeType){
var c = document.getElementById('myCanvas')
var ctx1=c.getContext("2d");
ctx1.fillStyle = "rgb(7,105,173)";
if(nodeType=="Root")
{
ctx1.fillRect(x-size/2,y-size/2,size,size);
ctx1.globalCompositeOperation = "destination-over"; //全局合成操作
// 绘制文字
ctx1.font="15px Arial";
// ctx1.fillText(nodeText, x+size/2+5, y+size/2-5);
ctx1.fillText(nodeText, x+size/2+5, y+size/2-5);
}
else if(nodeType=="Node")
{
ctx1.beginPath();
ctx1.arc(x,y,size,0,Math.PI*2);
ctx1.closePath();
ctx1.fill();
// 绘制文字
ctx1.font="15px Arial";
// ctx1.fillText(nodeText, x+size+5, y+size/2+5);
ctx1.fillText(nodeText, x+size+5, y+size/2+5);
}
}
// 正常树状线
function EdgInit(beginX,beginY,endX,endY){
var ctx1 = document.getElementById("myCanvas").getContext("2d");
ctx1.beginPath();
ctx1.moveTo(beginX, beginY);
ctx1.lineTo(endX,endY);
ctx1.lineWidth=1;
ctx1.strokeStyle="black";
ctx1.stroke();
ctx1.closePath();
}
// 垂直树状线
function EdgInit2(beginX,beginY,endX,endY)
{
var horizontalSpace =100 ;
var ctx1 = document.getElementById("myCanvas").getContext("2d");
ctx1.beginPath();
ctx1.moveTo(beginX, beginY);
ctx1.lineTo(beginX,beginY-horizontalSpace/2)
ctx1.lineTo(endX,beginY-horizontalSpace/2)
ctx1.lineTo(endX,endY);
ctx1.lineWidth=1;
ctx1.strokeStyle="black";
ctx1.stroke();
ctx1.closePath();
}
最后,这个算法最后也测试了一组一千个节点的数据,速度和显示上不存在任何问题。但是传统树状图在显示上还是有很多问题,比如造成严重的空间浪费等…所以后来有诸多学者提出了其他新颖的算法,去避免树状图在信息传达上的问题,比如径向树状图,空间的占用率更高。
同时关于本文所实现的树状图的完整算法
https://download.csdn.net/download/qq_41296039/21480959